Polynomial-Time Reachability for LTI Systems with Two-Level Lattice Neural Network Controllers

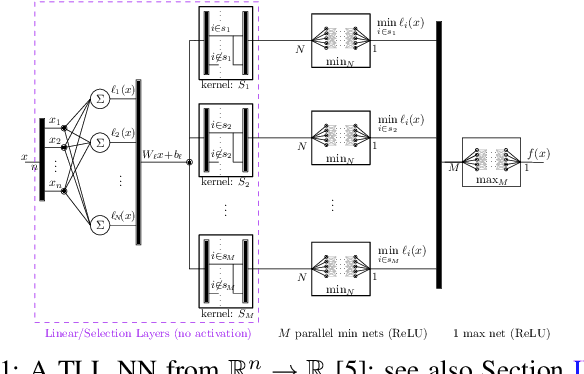
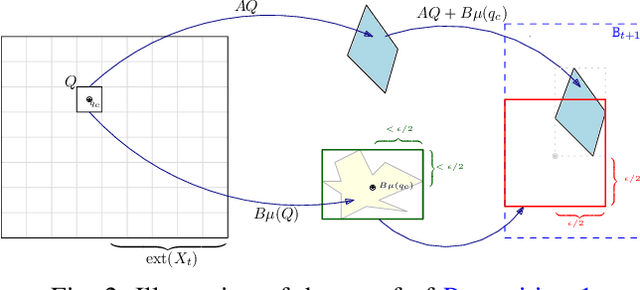
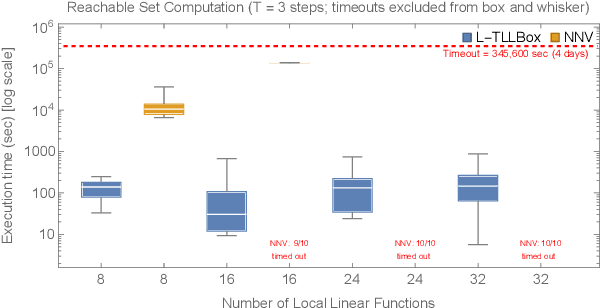
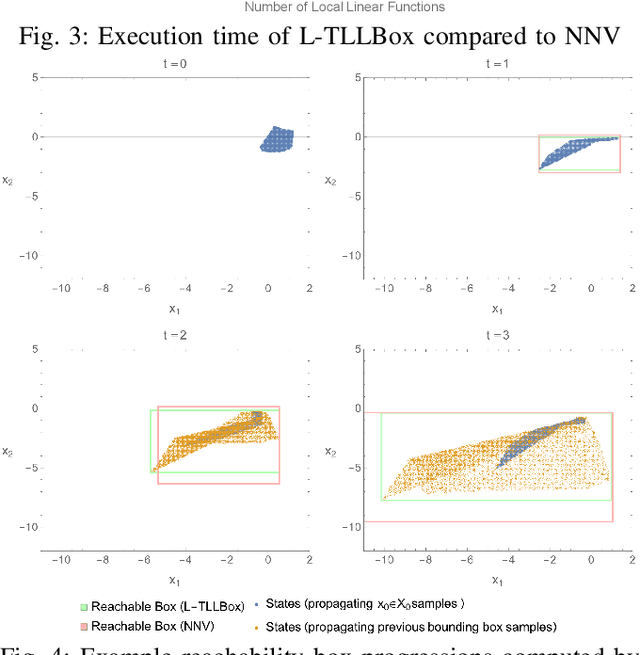
In this paper, we consider the computational complexity of bounding the reachable set of a Linear Time-Invariant (LTI) system controlled by a Rectified Linear Unit (ReLU) Two-Level Lattice (TLL) Neural Network (NN) controller. In particular, we show that for such a system and controller, it is possible to compute the exact one-step reachable set in polynomial time in the size of the size of the TLL NN controller (number of neurons). Additionally, we show that it is possible to obtain a tight bounding box of the reachable set via two polynomial-time methods: one with polynomial complexity in the size of the TLL and the other with polynomial complexity in the Lipschitz constant of the controller and other problem parameters. Crucially, the smaller of the two can be decided in polynomial time for non-degenerate TLL NNs. Finally, we propose a pragmatic algorithm that adaptively combines the benefits of (semi-)exact reachability and approximate reachability, which we call L-TLLBox. We evaluate L-TLLBox with an empirical comparison to a state-of-the-art NN controller reachability tool. In these experiments, L-TLLBox was able to complete reachability analysis as much as 5000x faster than this tool on the same network/system, while producing reach boxes that were from 0.08 to 1.42 times the area.