SAM 2: Segment Anything in Images and Videos

We present Segment Anything Model 2 (SAM 2), a foundation model towards solving promptable visual segmentation in images and videos. We build a data engine, which improves model and data via user interaction, to collect the largest video segmentation dataset to date. Our model is a simple transformer architecture with streaming memory for real-time video processing. SAM 2 trained on our data provides strong performance across a wide range of tasks. In video segmentation, we observe better accuracy, using 3x fewer interactions than prior approaches. In image segmentation, our model is more accurate and 6x faster than the Segment Anything Model (SAM). We believe that our data, model, and insights will serve as a significant milestone for video segmentation and related perception tasks. We are releasing a version of our model, the dataset and an interactive demo.

DeepBern-Nets: Taming the Complexity of Certifying Neural Networks using Bernstein Polynomial Activations and Precise Bound Propagation

Formal certification of Neural Networks (NNs) is crucial for ensuring their safety, fairness, and robustness. Unfortunately, on the one hand, sound and complete certification algorithms of ReLU-based NNs do not scale to large-scale NNs. On the other hand, incomplete certification algorithms are easier to compute, but they result in loose bounds that deteriorate with the depth of NN, which diminishes their effectiveness. In this paper, we ask the following question; can we replace the ReLU activation function with one that opens the door to incomplete certification algorithms that are easy to compute but can produce tight bounds on the NN's outputs? We introduce DeepBern-Nets, a class of NNs with activation functions based on Bernstein polynomials instead of the commonly used ReLU activation. Bernstein polynomials are smooth and differentiable functions with desirable properties such as the so-called range enclosure and subdivision properties. We design a novel algorithm, called Bern-IBP, to efficiently compute tight bounds on DeepBern-Nets outputs. Our approach leverages the properties of Bernstein polynomials to improve the tractability of neural network certification tasks while maintaining the accuracy of the trained networks. We conduct comprehensive experiments in adversarial robustness and reachability analysis settings to assess the effectiveness of the proposed Bernstein polynomial activation in enhancing the certification process. Our proposed framework achieves high certified accuracy for adversarially-trained NNs, which is often a challenging task for certifiers of ReLU-based NNs. Moreover, using Bern-IBP bounds for certified training results in NNs with state-of-the-art certified accuracy compared to ReLU networks. This work establishes Bernstein polynomial activation as a promising alternative for improving NN certification tasks across various applications.

BERN-NN: Tight Bound Propagation For Neural Networks Using Bernstein Polynomial Interval Arithmetic

In this paper, we present BERN-NN as an efficient tool to perform bound propagation of Neural Networks (NNs). Bound propagation is a critical step in wide range of NN model checkers and reachability analysis tools. Given a bounded input set, bound propagation algorithms aim to compute tight bounds on the output of the NN. So far, linear and convex optimizations have been used to perform bound propagation. Since neural networks are highly non-convex, state-of-the-art bound propagation techniques suffer from introducing large errors. To circumvent such drawback, BERN-NN approximates the bounds of each neuron using a class of polynomials called Bernstein polynomials. Bernstein polynomials enjoy several interesting properties that allow BERN-NN to obtain tighter bounds compared to those relying on linear and convex approximations. BERN-NN is efficiently parallelized on graphic processing units (GPUs). Extensive numerical results show that bounds obtained by BERN-NN are orders of magnitude tighter than those obtained by state-of-the-art verifiers such as linear programming and linear interval arithmetic. Moreoveer, BERN-NN is both faster and produces tighter outputs compared to convex programming approaches like alpha-CROWN.

CertiFair: A Framework for Certified Global Fairness of Neural Networks

We consider the problem of whether a Neural Network (NN) model satisfies global individual fairness. Individual Fairness suggests that similar individuals with respect to a certain task are to be treated similarly by the decision model. In this work, we have two main objectives. The first is to construct a verifier which checks whether the fairness property holds for a given NN in a classification task or provide a counterexample if it is violated, i.e., the model is fair if all similar individuals are classified the same, and unfair if a pair of similar individuals are classified differently. To that end, We construct a sound and complete verifier that verifies global individual fairness properties of ReLU NN classifiers using distance-based similarity metrics. The second objective of this paper is to provide a method for training provably fair NN classifiers from unfair (biased) data. We propose a fairness loss that can be used during training to enforce fair outcomes for similar individuals. We then provide provable bounds on the fairness of the resulting NN. We run experiments on commonly used fairness datasets that are publicly available and we show that global individual fairness can be improved by 96 % without significant drop in test accuracy.

Fast BATLLNN: Fast Box Analysis of Two-Level Lattice Neural Networks

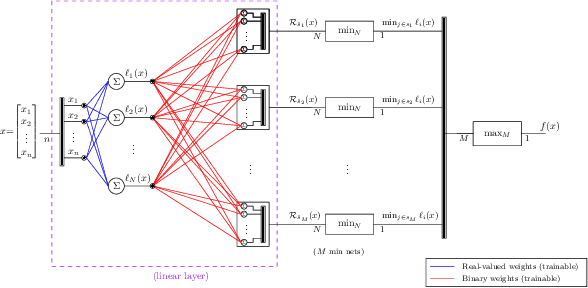
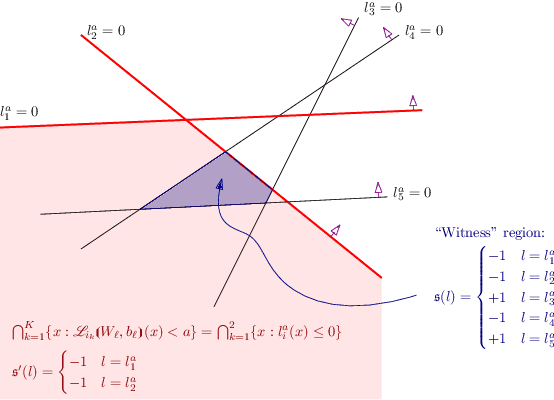
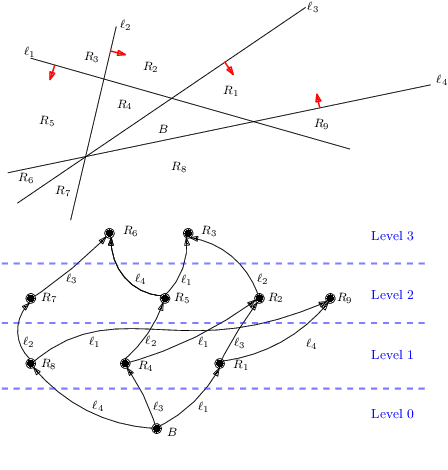
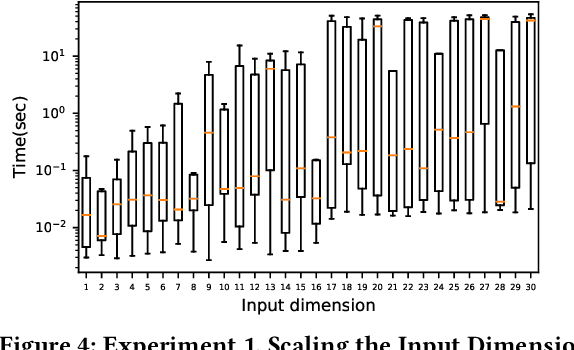
In this paper, we present the tool Fast Box Analysis of Two-Level Lattice Neural Networks (Fast BATLLNN) as a fast verifier of box-like output constraints for Two-Level Lattice (TLL) Neural Networks (NNs). In particular, Fast BATLLNN can verify whether the output of a given TLL NN always lies within a specified hyper-rectangle whenever its input constrained to a specified convex polytope (not necessarily a hyper-rectangle). Fast BATLLNN uses the unique semantics of the TLL architecture and the decoupled nature of box-like output constraints to dramatically improve verification performance relative to known polynomial-time verification algorithms for TLLs with generic polytopic output constraints. In this paper, we evaluate the performance and scalability of Fast BATLLNN, both in its own right and compared to state-of-the-art NN verifiers applied to TLL NNs. Fast BATLLNN compares very favorably to even the fastest NN verifiers, completing our synthetic TLL test bench more than 400x faster than its nearest competitor.

Effective Formal Verification of Neural Networks using the Geometry of Linear Regions

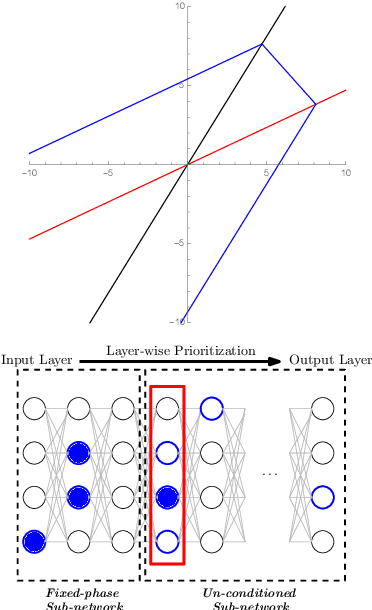
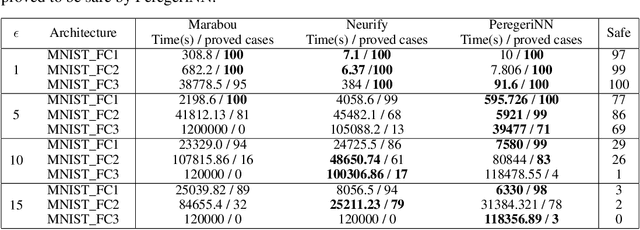
Neural Networks (NNs) have increasingly apparent safety implications commensurate with their proliferation in real-world applications: both unanticipated as well as adversarial misclassifications can result in fatal outcomes. As a consequence, techniques of formal verification have been recognized as crucial to the design and deployment of safe NNs. In this paper, we introduce a new approach to formally verify the most commonly considered safety specification for ReLU NNs -- i.e. polytopic specifications on the input and output of the network. Like some other approaches, ours uses a relaxed convex program to mitigate the combinatorial complexity of the problem. However, unique in our approach is the way we exploit the geometry of neuronal activation regions to further prune the search space of relaxed neuron activations. In particular, conditioning on neurons from input layer to output layer, we can regard each relaxed neuron as having the simplest possible geometry for its activation region: a half-space.This paradigm can be leveraged to create a verification algorithm that is not only faster in general than competing approaches, but is also able to verify considerably more safety properties. For example, our approach completes the standard MNIST verification test bench 2.7-50 times faster than competing algorithms while still proving 14-30% more properties. We also used our framework to verify the safety of a neural network controlled autonomous robot in a structured environment, and observed a 1900 times speed up compared to existing methods.

Formal Verification of Neural Network Controlled Autonomous Systems

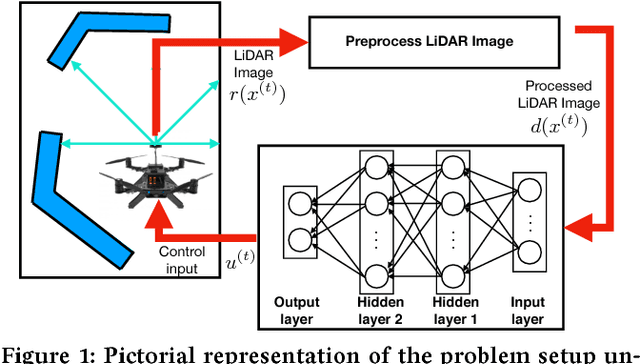
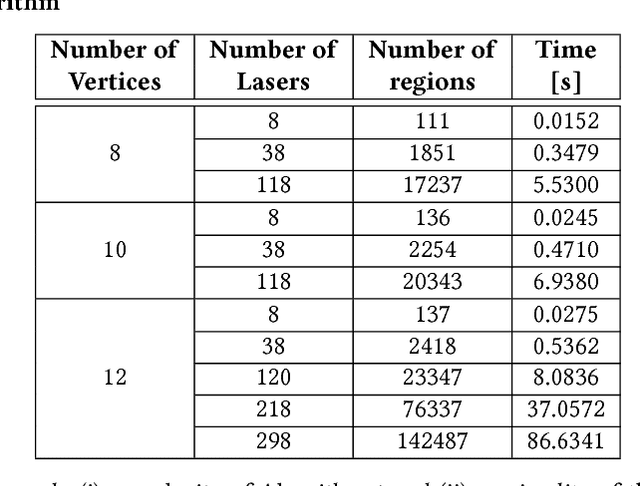
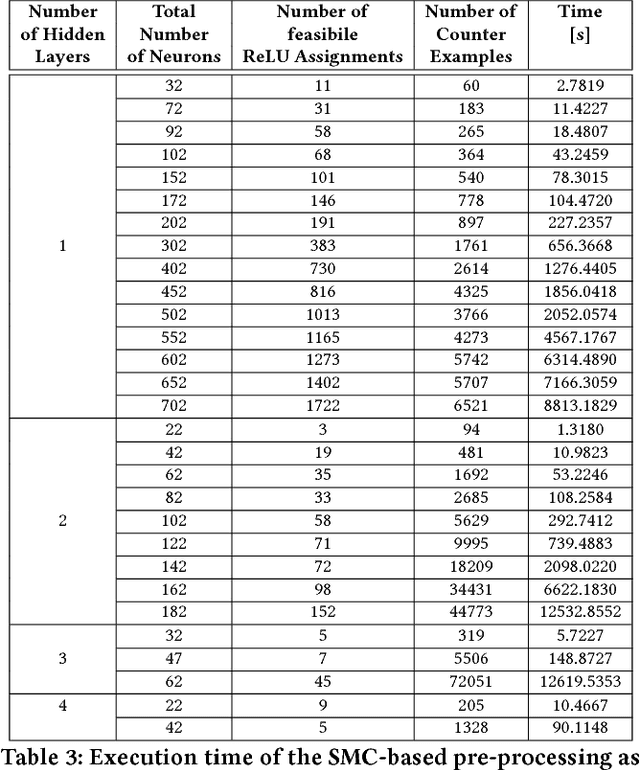
In this paper, we consider the problem of formally verifying the safety of an autonomous robot equipped with a Neural Network (NN) controller that processes LiDAR images to produce control actions. Given a workspace that is characterized by a set of polytopic obstacles, our objective is to compute the set of safe initial conditions such that a robot trajectory starting from these initial conditions is guaranteed to avoid the obstacles. Our approach is to construct a finite state abstraction of the system and use standard reachability analysis over the finite state abstraction to compute the set of the safe initial states. The first technical problem in computing the finite state abstraction is to mathematically model the imaging function that maps the robot position to the LiDAR image. To that end, we introduce the notion of imaging-adapted sets as partitions of the workspace in which the imaging function is guaranteed to be affine. We develop a polynomial-time algorithm to partition the workspace into imaging-adapted sets along with computing the corresponding affine imaging functions. Given this workspace partitioning, a discrete-time linear dynamics of the robot, and a pre-trained NN controller with Rectified Linear Unit (ReLU) nonlinearity, the second technical challenge is to analyze the behavior of the neural network. To that end, we utilize a Satisfiability Modulo Convex (SMC) encoding to enumerate all the possible segments of different ReLUs. SMC solvers then use a Boolean satisfiability solver and a convex programming solver and decompose the problem into smaller subproblems. To accelerate this process, we develop a pre-processing algorithm that could rapidly prune the space feasible ReLU segments. Finally, we demonstrate the efficiency of the proposed algorithms using numerical simulations with increasing complexity of the neural network controller.