Formal Verification of Neural Network Controlled Autonomous Systems
Paper and Code
Oct 31, 2018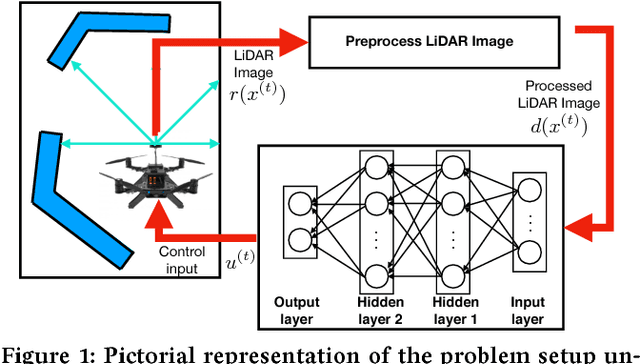
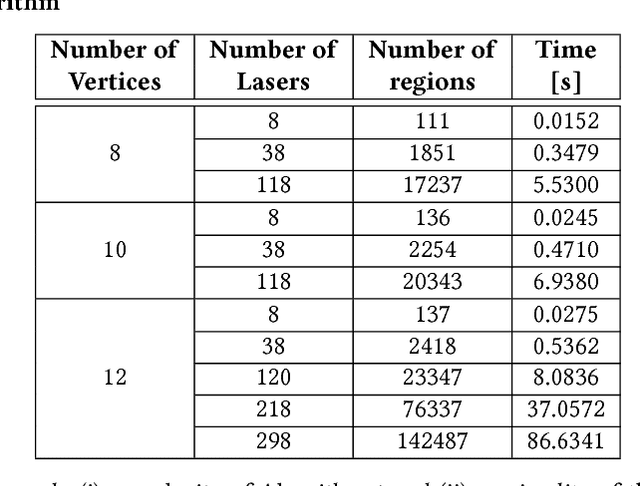

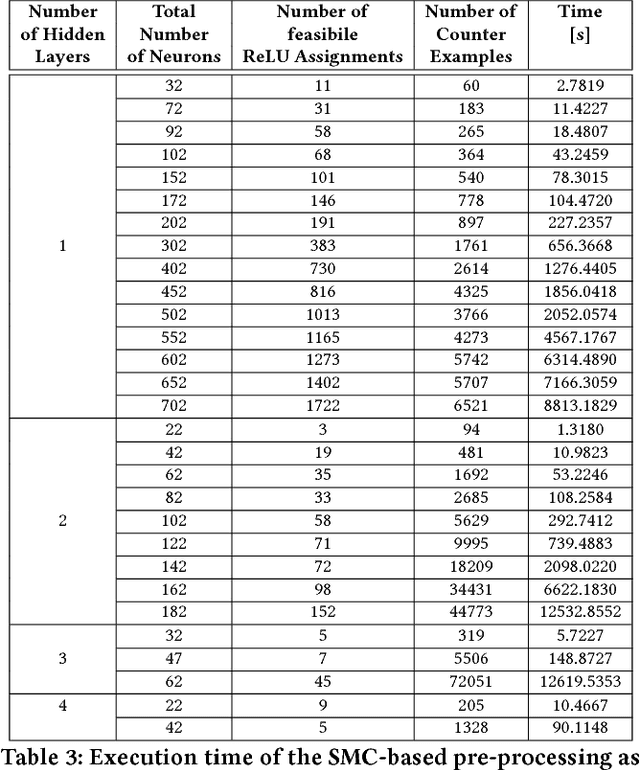
In this paper, we consider the problem of formally verifying the safety of an autonomous robot equipped with a Neural Network (NN) controller that processes LiDAR images to produce control actions. Given a workspace that is characterized by a set of polytopic obstacles, our objective is to compute the set of safe initial conditions such that a robot trajectory starting from these initial conditions is guaranteed to avoid the obstacles. Our approach is to construct a finite state abstraction of the system and use standard reachability analysis over the finite state abstraction to compute the set of the safe initial states. The first technical problem in computing the finite state abstraction is to mathematically model the imaging function that maps the robot position to the LiDAR image. To that end, we introduce the notion of imaging-adapted sets as partitions of the workspace in which the imaging function is guaranteed to be affine. We develop a polynomial-time algorithm to partition the workspace into imaging-adapted sets along with computing the corresponding affine imaging functions. Given this workspace partitioning, a discrete-time linear dynamics of the robot, and a pre-trained NN controller with Rectified Linear Unit (ReLU) nonlinearity, the second technical challenge is to analyze the behavior of the neural network. To that end, we utilize a Satisfiability Modulo Convex (SMC) encoding to enumerate all the possible segments of different ReLUs. SMC solvers then use a Boolean satisfiability solver and a convex programming solver and decompose the problem into smaller subproblems. To accelerate this process, we develop a pre-processing algorithm that could rapidly prune the space feasible ReLU segments. Finally, we demonstrate the efficiency of the proposed algorithms using numerical simulations with increasing complexity of the neural network controller.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge