BERN-NN: Tight Bound Propagation For Neural Networks Using Bernstein Polynomial Interval Arithmetic

In this paper, we present BERN-NN as an efficient tool to perform bound propagation of Neural Networks (NNs). Bound propagation is a critical step in wide range of NN model checkers and reachability analysis tools. Given a bounded input set, bound propagation algorithms aim to compute tight bounds on the output of the NN. So far, linear and convex optimizations have been used to perform bound propagation. Since neural networks are highly non-convex, state-of-the-art bound propagation techniques suffer from introducing large errors. To circumvent such drawback, BERN-NN approximates the bounds of each neuron using a class of polynomials called Bernstein polynomials. Bernstein polynomials enjoy several interesting properties that allow BERN-NN to obtain tighter bounds compared to those relying on linear and convex approximations. BERN-NN is efficiently parallelized on graphic processing units (GPUs). Extensive numerical results show that bounds obtained by BERN-NN are orders of magnitude tighter than those obtained by state-of-the-art verifiers such as linear programming and linear interval arithmetic. Moreoveer, BERN-NN is both faster and produces tighter outputs compared to convex programming approaches like alpha-CROWN.

Provably Safe Model-Based Meta Reinforcement Learning: An Abstraction-Based Approach

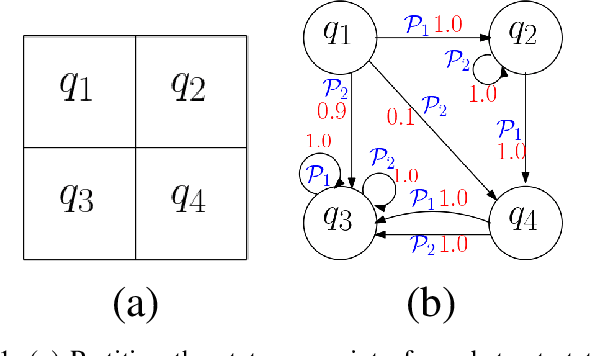
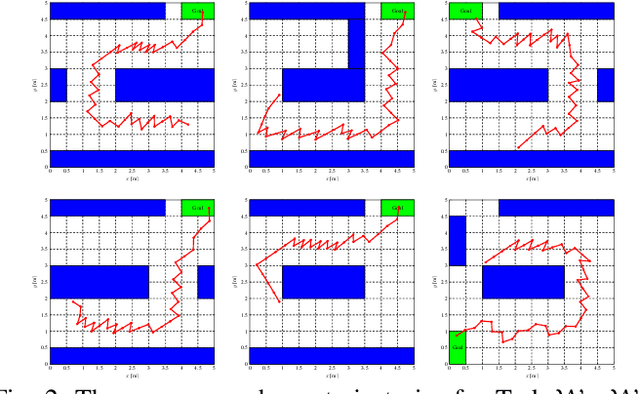
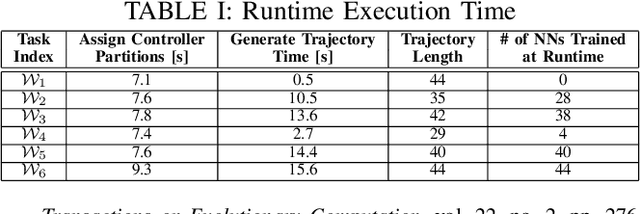
While conventional reinforcement learning focuses on designing agents that can perform one task, meta-learning aims, instead, to solve the problem of designing agents that can generalize to different tasks (e.g., environments, obstacles, and goals) that were not considered during the design or the training of these agents. In this spirit, in this paper, we consider the problem of training a provably safe Neural Network (NN) controller for uncertain nonlinear dynamical systems that can generalize to new tasks that were not present in the training data while preserving strong safety guarantees. Our approach is to learn a set of NN controllers during the training phase. When the task becomes available at runtime, our framework will carefully select a subset of these NN controllers and compose them to form the final NN controller. Critical to our approach is the ability to compute a finite-state abstraction of the nonlinear dynamical system. This abstract model captures the behavior of the closed-loop system under all possible NN weights, and is used to train the NNs and compose them when the task becomes available. We provide theoretical guarantees that govern the correctness of the resulting NN. We evaluated our approach on the problem of controlling a wheeled robot in cluttered environments that were not present in the training data.