Effective Formal Verification of Neural Networks using the Geometry of Linear Regions

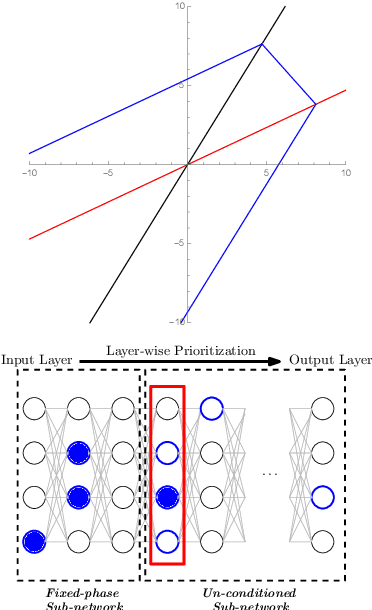
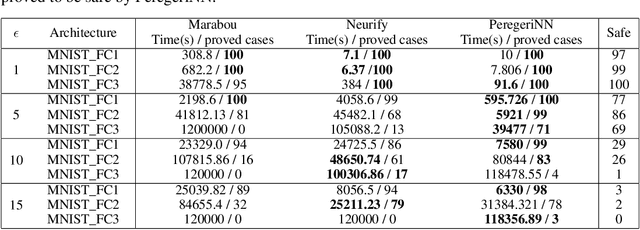
Neural Networks (NNs) have increasingly apparent safety implications commensurate with their proliferation in real-world applications: both unanticipated as well as adversarial misclassifications can result in fatal outcomes. As a consequence, techniques of formal verification have been recognized as crucial to the design and deployment of safe NNs. In this paper, we introduce a new approach to formally verify the most commonly considered safety specification for ReLU NNs -- i.e. polytopic specifications on the input and output of the network. Like some other approaches, ours uses a relaxed convex program to mitigate the combinatorial complexity of the problem. However, unique in our approach is the way we exploit the geometry of neuronal activation regions to further prune the search space of relaxed neuron activations. In particular, conditioning on neurons from input layer to output layer, we can regard each relaxed neuron as having the simplest possible geometry for its activation region: a half-space.This paradigm can be leveraged to create a verification algorithm that is not only faster in general than competing approaches, but is also able to verify considerably more safety properties. For example, our approach completes the standard MNIST verification test bench 2.7-50 times faster than competing algorithms while still proving 14-30% more properties. We also used our framework to verify the safety of a neural network controlled autonomous robot in a structured environment, and observed a 1900 times speed up compared to existing methods.