Granite-speech: open-source speech-aware LLMs with strong English ASR capabilities

Granite-speech LLMs are compact and efficient speech language models specifically designed for English ASR and automatic speech translation (AST). The models were trained by modality aligning the 2B and 8B parameter variants of granite-3.3-instruct to speech on publicly available open-source corpora containing audio inputs and text targets consisting of either human transcripts for ASR or automatically generated translations for AST. Comprehensive benchmarking shows that on English ASR, which was our primary focus, they outperform several competitors' models that were trained on orders of magnitude more proprietary data, and they keep pace on English-to-X AST for major European languages, Japanese, and Chinese. The speech-specific components are: a conformer acoustic encoder using block attention and self-conditioning trained with connectionist temporal classification, a windowed query-transformer speech modality adapter used to do temporal downsampling of the acoustic embeddings and map them to the LLM text embedding space, and LoRA adapters to further fine-tune the text LLM. Granite-speech-3.3 operates in two modes: in speech mode, it performs ASR and AST by activating the encoder, projector, and LoRA adapters; in text mode, it calls the underlying granite-3.3-instruct model directly (without LoRA), essentially preserving all the text LLM capabilities and safety. Both models are freely available on HuggingFace (https://huggingface.co/ibm-granite/granite-speech-3.3-2b and https://huggingface.co/ibm-granite/granite-speech-3.3-8b) and can be used for both research and commercial purposes under a permissive Apache 2.0 license.

Accelerated Reeds-Shepp and Under-Specified Reeds-Shepp Algorithms for Mobile Robot Path Planning

In this study, we present a simple and intuitive method for accelerating optimal Reeds-Shepp path computation. Our approach uses geometrical reasoning to analyze the behavior of optimal paths, resulting in a new partitioning of the state space and a further reduction in the minimal set of viable paths. We revisit and reimplement classic methodologies from the literature, which lack contemporary open-source implementations, to serve as benchmarks for evaluating our method. Additionally, we address the under-specified Reeds-Shepp planning problem where the final orientation is unspecified. We perform exhaustive experiments to validate our solutions. Compared to the modern C++ implementation of the original Reeds-Shepp solution in the Open Motion Planning Library, our method demonstrates a 15x speedup, while classic methods achieve a 5.79x speedup. Both approaches exhibit machine-precision differences in path lengths compared to the original solution. We release our proposed C++ implementations for both the accelerated and under-specified Reeds-Shepp problems as open-source code.

Exact Wavefront Propagation for Globally Optimal One-to-All Path Planning on 2D Cartesian Grids

This paper introduces an efficient $\mathcal{O}(n)$ compute and memory complexity algorithm for globally optimal path planning on 2D Cartesian grids. Unlike existing marching methods that rely on approximate discretized solutions to the Eikonal equation, our approach achieves exact wavefront propagation by pivoting the analytic distance function based on visibility. The algorithm leverages a dynamic-programming subroutine to efficiently evaluate visibility queries. Through benchmarking against state-of-the-art any-angle path planners, we demonstrate that our method outperforms existing approaches in both speed and accuracy, particularly in cluttered environments. Notably, our method inherently provides globally optimal paths to all grid points, eliminating the need for additional gradient descent steps per path query. The same capability extends to multiple starting positions. We also provide a greedy version of our algorithm as well as open-source C++ implementation of our solver.

An Efficient Solution to the 2D Visibility Problem in Cartesian Grid Maps and its Application in Heuristic Path Planning

This paper introduces a novel, lightweight method to solve the visibility problem for 2D grids. The proposed method evaluates the existence of lines-of-sight from a source point to all other grid cells in a single pass with no preprocessing and independently of the number and shape of obstacles. It has a compute and memory complexity of $\mathcal{O}(n)$, where $n = n_{x}\times{} n_{y}$ is the size of the grid, and requires at most ten arithmetic operations per grid cell. In the proposed approach, we use a linear first-order hyperbolic partial differential equation to transport the visibility quantity in all directions. In order to accomplish that, we use an entropy-satisfying upwind scheme that converges to the true visibility polygon as the step size goes to zero. This dynamic-programming approach allows the evaluation of visibility for an entire grid orders of magnitude faster than typical ray-casting algorithms. We provide a practical application of our proposed algorithm by posing the visibility quantity as a heuristic and implementing a deterministic, local-minima-free path planner, setting apart the proposed planner from traditional methods. Lastly, we provide necessary algorithms and an open-source implementation of the proposed methods.

Whole-Body MPC and Dynamic Occlusion Avoidance: A Maximum Likelihood Visibility Approach

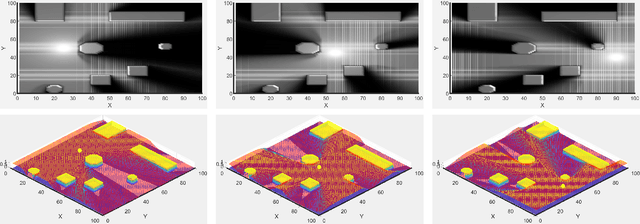
This paper introduces a novel approach for whole-body motion planning and dynamic occlusion avoidance. The proposed approach reformulates the visibility constraint as a likelihood maximization of visibility probability. In this formulation, we augment the primary cost function of a whole-body model predictive control scheme through a relaxed log barrier function yielding a relaxed log-likelihood maximization formulation of visibility probability. The visibility probability is computed through a probabilistic shadow field that quantifies point light source occlusions. We provide the necessary algorithms to obtain such a field for both 2D and 3D cases. We demonstrate 2D implementations of this field in simulation and 3D implementations through real-time hardware experiments. We show that due to the linear complexity of our shadow field algorithm to the map size, we can achieve high update rates, which facilitates onboard execution on mobile platforms with limited computational power. Lastly, we evaluate the performance of the proposed MPC reformulation in simulation for a quadrupedal mobile manipulator.