Equivariant neural networks for recovery of Hadamard matrices

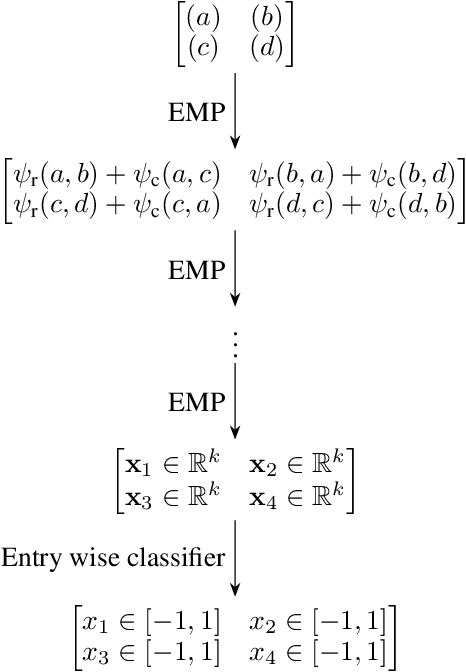
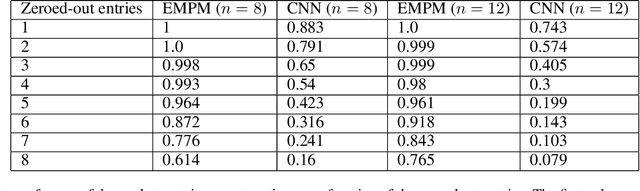
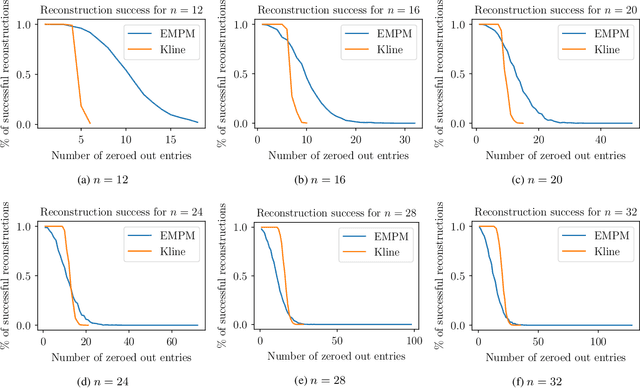
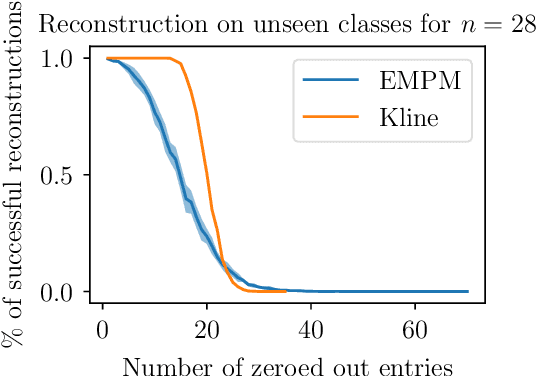
We propose a message passing neural network architecture designed to be equivariant to column and row permutations of a matrix. We illustrate its advantages over traditional architectures like multi-layer perceptrons (MLPs), convolutional neural networks (CNNs) and even Transformers, on the combinatorial optimization task of recovering a set of deleted entries of a Hadamard matrix. We argue that this is a powerful application of the principles of Geometric Deep Learning to fundamental mathematics, and a potential stepping stone toward more insights on the Hadamard conjecture using Machine Learning techniques.

Adaptive Temporal-Difference Learning for Policy Evaluation with Per-State Uncertainty Estimates

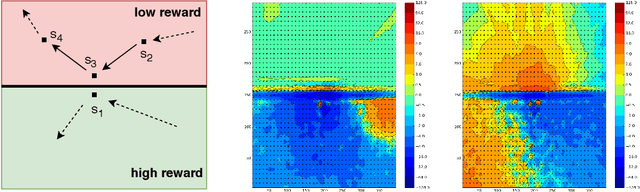
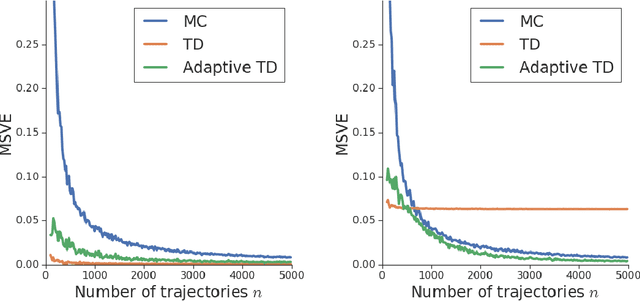
We consider the core reinforcement-learning problem of on-policy value function approximation from a batch of trajectory data, and focus on various issues of Temporal Difference (TD) learning and Monte Carlo (MC) policy evaluation. The two methods are known to achieve complementary bias-variance trade-off properties, with TD tending to achieve lower variance but potentially higher bias. In this paper, we argue that the larger bias of TD can be a result of the amplification of local approximation errors. We address this by proposing an algorithm that adaptively switches between TD and MC in each state, thus mitigating the propagation of errors. Our method is based on learned confidence intervals that detect biases of TD estimates. We demonstrate in a variety of policy evaluation tasks that this simple adaptive algorithm performs competitively with the best approach in hindsight, suggesting that learned confidence intervals are a powerful technique for adapting policy evaluation to use TD or MC returns in a data-driven way.

Temporal Difference Learning with Neural Networks - Study of the Leakage Propagation Problem

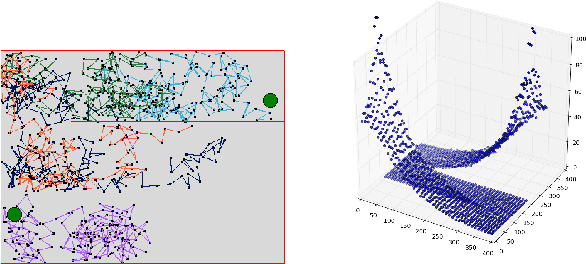
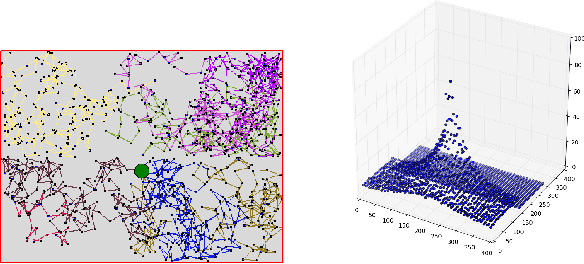
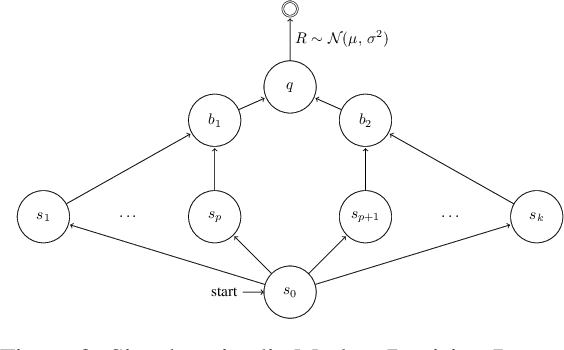
Temporal-Difference learning (TD) [Sutton, 1988] with function approximation can converge to solutions that are worse than those obtained by Monte-Carlo regression, even in the simple case of on-policy evaluation. To increase our understanding of the problem, we investigate the issue of approximation errors in areas of sharp discontinuities of the value function being further propagated by bootstrap updates. We show empirical evidence of this leakage propagation, and show analytically that it must occur, in a simple Markov chain, when function approximation errors are present. For reversible policies, the result can be interpreted as the tension between two terms of the loss function that TD minimises, as recently described by [Ollivier, 2018]. We show that the upper bounds from [Tsitsiklis and Van Roy, 1997] hold, but they do not imply that leakage propagation occurs and under what conditions. Finally, we test whether the problem could be mitigated with a better state representation, and whether it can be learned in an unsupervised manner, without rewards or privileged information.

Adaptive Lambda Least-Squares Temporal Difference Learning

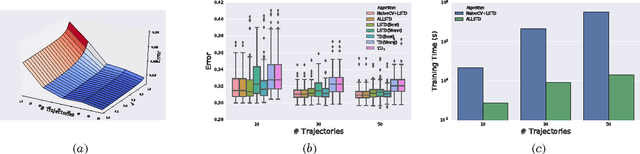
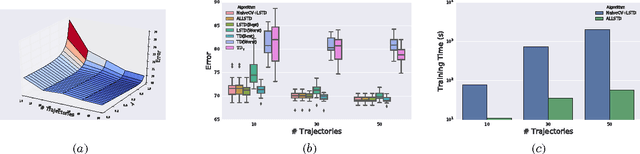
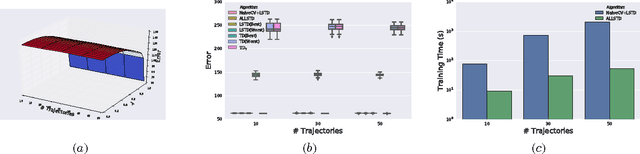
Temporal Difference learning or TD($\lambda$) is a fundamental algorithm in the field of reinforcement learning. However, setting TD's $\lambda$ parameter, which controls the timescale of TD updates, is generally left up to the practitioner. We formalize the $\lambda$ selection problem as a bias-variance trade-off where the solution is the value of $\lambda$ that leads to the smallest Mean Squared Value Error (MSVE). To solve this trade-off we suggest applying Leave-One-Trajectory-Out Cross-Validation (LOTO-CV) to search the space of $\lambda$ values. Unfortunately, this approach is too computationally expensive for most practical applications. For Least Squares TD (LSTD) we show that LOTO-CV can be implemented efficiently to automatically tune $\lambda$ and apply function optimization methods to efficiently search the space of $\lambda$ values. The resulting algorithm, ALLSTD, is parameter free and our experiments demonstrate that ALLSTD is significantly computationally faster than the na\"{i}ve LOTO-CV implementation while achieving similar performance.