Decoupling Inference from State Updates in Low-Latency Feature Engines via Probabilistic Thinning

Streaming data systems increasingly underpin Machine Learning workflows that maintain large numbers of continuously updated aggregations. In production settings, each incoming event typically triggers read-modify-write operations to persistent storage, making high-frequency state updates a dominant source of latency, contention, and operational cost. In this work, we decouple inference from state persistence in streaming Machine Learning pipelines via probabilistic thinning: every event is scored, but durable state updates are selectively triggered by informative events. Unlike approaches that shed input or state, we show that persistence-path control is achievable without a high-frequency in-memory control plane or cross-worker coordination, relying exclusively on approximate statistics retrieved from disk-backed key-value stores. We model the resulting stochastic processes, derive bounds on filtering rates, and prove that common time-based aggregations remain unbiased under variance-aware formulations, preventing systemic error accumulation. We evaluate the approach in a controlled setting that isolates per-event costs, demonstrating substantial reductions in storage Input/Output and serialization overhead. Across experiments, up to 90% of events are excluded from the persistence path while preserving and in some cases improving downstream utility.

Equivariant neural networks for recovery of Hadamard matrices

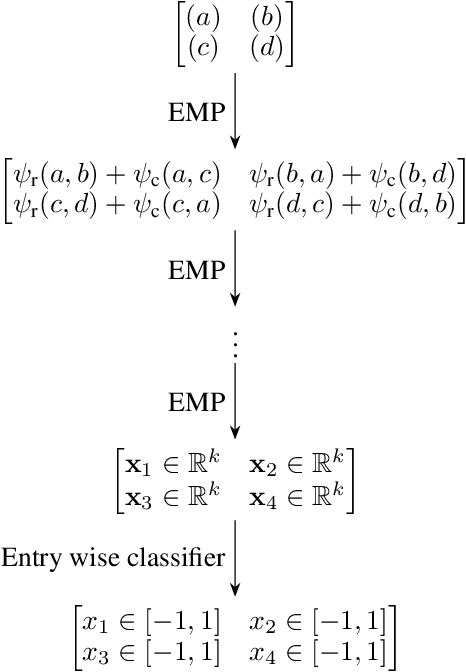
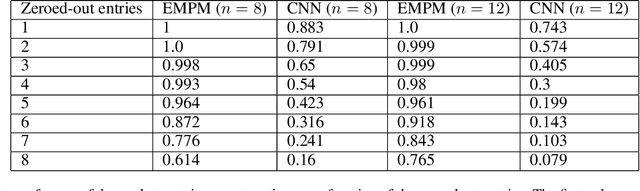
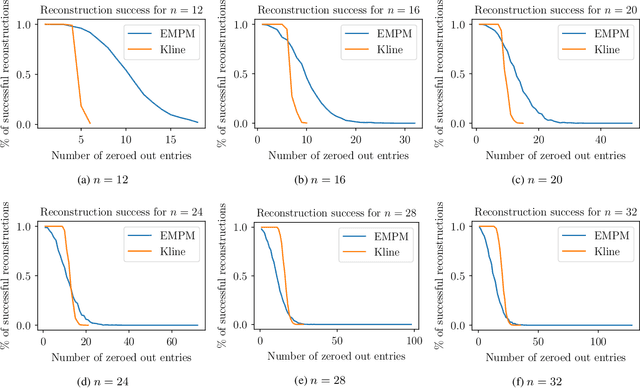
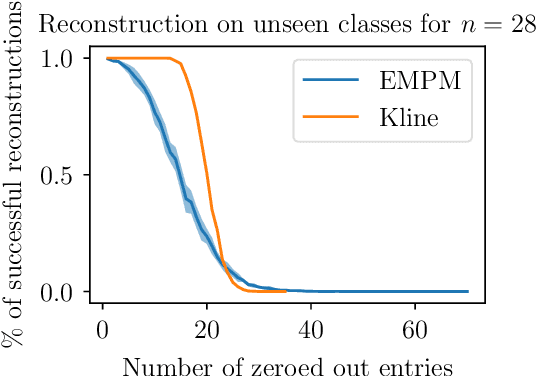
We propose a message passing neural network architecture designed to be equivariant to column and row permutations of a matrix. We illustrate its advantages over traditional architectures like multi-layer perceptrons (MLPs), convolutional neural networks (CNNs) and even Transformers, on the combinatorial optimization task of recovering a set of deleted entries of a Hadamard matrix. We argue that this is a powerful application of the principles of Geometric Deep Learning to fundamental mathematics, and a potential stepping stone toward more insights on the Hadamard conjecture using Machine Learning techniques.