Huan Long
Electricity Price Prediction for Energy Storage System Arbitrage: A Decision-focused Approach
Apr 30, 2023



Abstract:Electricity price prediction plays a vital role in energy storage system (ESS) management. Current prediction models focus on reducing prediction errors but overlook their impact on downstream decision-making. So this paper proposes a decision-focused electricity price prediction approach for ESS arbitrage to bridge the gap from the downstream optimization model to the prediction model. The decision-focused approach aims at utilizing the downstream arbitrage model for training prediction models. It measures the difference between actual decisions under the predicted price and oracle decisions under the true price, i.e., decision error, by regret, transforms it into the tractable surrogate regret, and then derives the gradients to predicted price for training prediction models. Based on the prediction and decision errors, this paper proposes the hybrid loss and corresponding stochastic gradient descent learning method to learn prediction models for prediction and decision accuracy. The case study verifies that the proposed approach can efficiently bring more economic benefits and reduce decision errors by flattening the time distribution of prediction errors, compared to prediction models for only minimizing prediction errors.
On Geometric Structure of Activation Spaces in Neural Networks
Apr 02, 2019



Abstract:In this paper, we investigate the geometric structure of activation spaces of fully connected layers in neural networks and then show applications of this study. We propose an efficient approximation algorithm to characterize the convex hull of massive points in high dimensional space. Based on this new algorithm, four common geometric properties shared by the activation spaces are concluded, which gives a rather clear description of the activation spaces. We then propose an alternative classification method grounding on the geometric structure description, which works better than neural networks alone. Surprisingly, this data classification method can be an indicator of overfitting in neural networks. We believe our work reveals several critical intrinsic properties of modern neural networks and further gives a new metric for evaluating them.
Knowledge-based Fully Convolutional Network and Its Application in Segmentation of Lung CT Images
May 22, 2018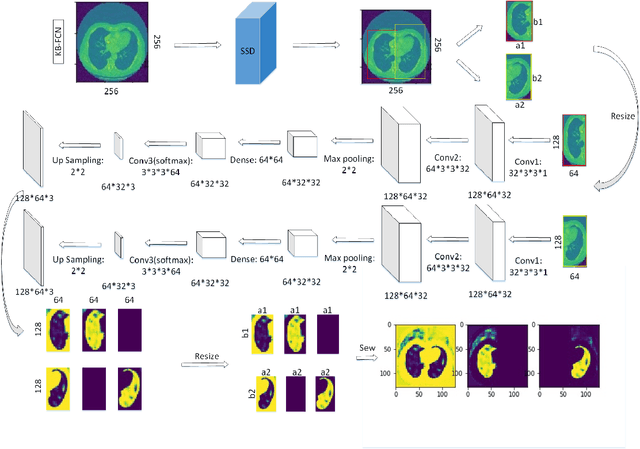
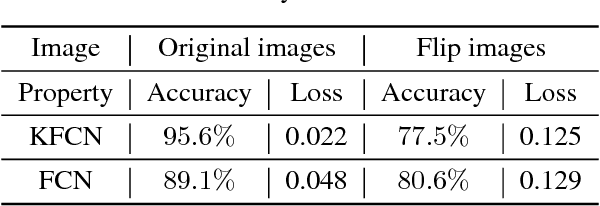


Abstract:A variety of deep neural networks have been applied in medical image segmentation and achieve good performance. Unlike natural images, medical images of the same imaging modality are characterized by the same pattern, which indicates that same normal organs or tissues locate at similar positions in the images. Thus, in this paper we try to incorporate the prior knowledge of medical images into the structure of neural networks such that the prior knowledge can be utilized for accurate segmentation. Based on this idea, we propose a novel deep network called knowledge-based fully convolutional network (KFCN) for medical image segmentation. The segmentation function and corresponding error is analyzed. We show the existence of an asymptotically stable region for KFCN which traditional FCN doesn't possess. Experiments validate our knowledge assumption about the incorporation of prior knowledge into the convolution kernels of KFCN and show that KFCN can achieve a reasonable segmentation and a satisfactory accuracy.
Curvature-based Comparison of Two Neural Networks
Jan 21, 2018
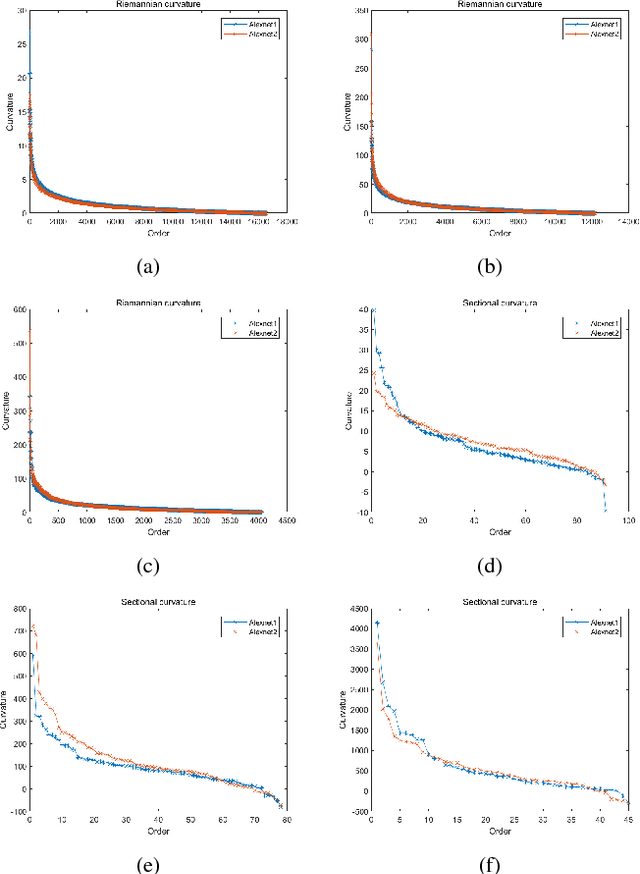

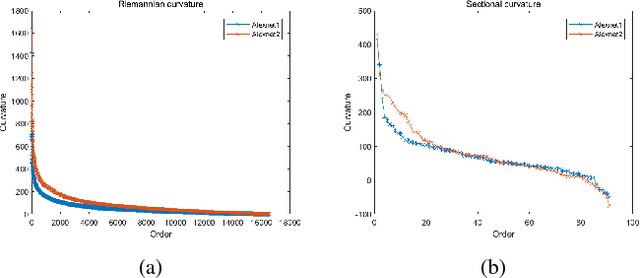
Abstract:In this paper we show the similarities and differences of two deep neural networks by comparing the manifolds composed of activation vectors in each fully connected layer of them. The main contribution of this paper includes 1) a new data generating algorithm which is crucial for determining the dimension of manifolds; 2) a systematic strategy to compare manifolds. Especially, we take Riemann curvature and sectional curvature as part of criterion, which can reflect the intrinsic geometric properties of manifolds. Some interesting results and phenomenon are given, which help in specifying the similarities and differences between the features extracted by two networks and demystifying the intrinsic mechanism of deep neural networks.
The Local Dimension of Deep Manifold
Nov 05, 2017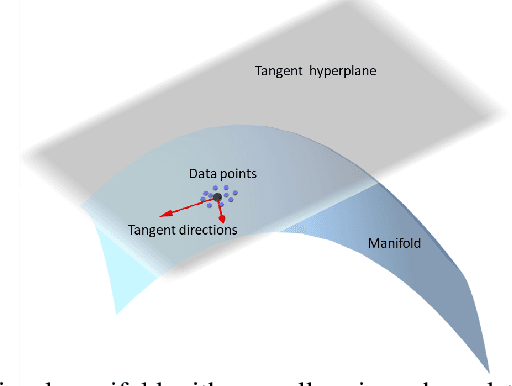



Abstract:Based on our observation that there exists a dramatic drop for the singular values of the fully connected layers or a single feature map of the convolutional layer, and that the dimension of the concatenated feature vector almost equals the summation of the dimension on each feature map, we propose a singular value decomposition (SVD) based approach to estimate the dimension of the deep manifolds for a typical convolutional neural network VGG19. We choose three categories from the ImageNet, namely Persian Cat, Container Ship and Volcano, and determine the local dimension of the deep manifolds of the deep layers through the tangent space of a target image. Through several augmentation methods, we found that the Gaussian noise method is closer to the intrinsic dimension, as by adding random noise to an image we are moving in an arbitrary dimension, and when the rank of the feature matrix of the augmented images does not increase we are very close to the local dimension of the manifold. We also estimate the dimension of the deep manifold based on the tangent space for each of the maxpooling layers. Our results show that the dimensions of different categories are close to each other and decline quickly along the convolutional layers and fully connected layers. Furthermore, we show that the dimensions decline quickly inside the Conv5 layer. Our work provides new insights for the intrinsic structure of deep neural networks and helps unveiling the inner organization of the black box of deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge