Reasoning through Verifiable Forecast Actions: Consistency-Grounded RL for Financial LLMs

Financial markets are characterized by extreme non-stationarity, low signal-to-noise ratios, and strong dependence on external information such as news, company fundamentals, and macroeconomic signals. Yet, existing approaches either abstract time-series into text or decouple forecasting from language-based reasoning, leading to a fundamental mismatch between qualitative reasoning and quantitative outcomes. To address this, we introduce StockR1, a time-series-enhanced LLM that unifies stock forecasting and financial reasoning through a verifiable forecast action. Based on a tool-call design, the model first emits a forecast action, which is a structured and interpretable representation of its qualitative market outlook. It then invokes a time-series decoder conditioned on this action to generate distributional future trajectories, leading to more informed question answering and financial reasoning. We optimize the full pipeline with reinforcement learning, where rewards jointly reflect answer validity, forecast accuracy, and consistency between generated actions and observed time-series dynamics. In addition, rewards are reweighted by a sample-level uncertainty scalar, encouraging the model to accommodate varying uncertainty in market dynamics. We evaluate StockR1 on financial question answering and stock forecasting over a large-scale 10-year benchmark. Our method consistently outperforms time-series baselines and general-purpose LLMs, improving reasoning accuracy by 17.7% (4B) and 25.9% (8B). These findings demonstrate that structuring the forecast actions establishes a powerful synergy between language reasoning and temporal prediction, enabling LLMs to reason through verifiable, interpretable, and numerically grounded decisions.

AceMap: Knowledge Discovery through Academic Graph

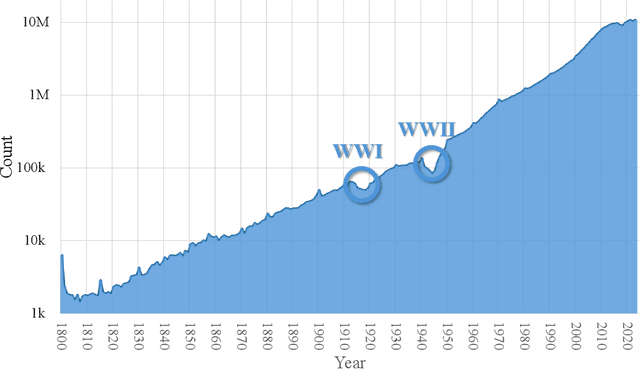
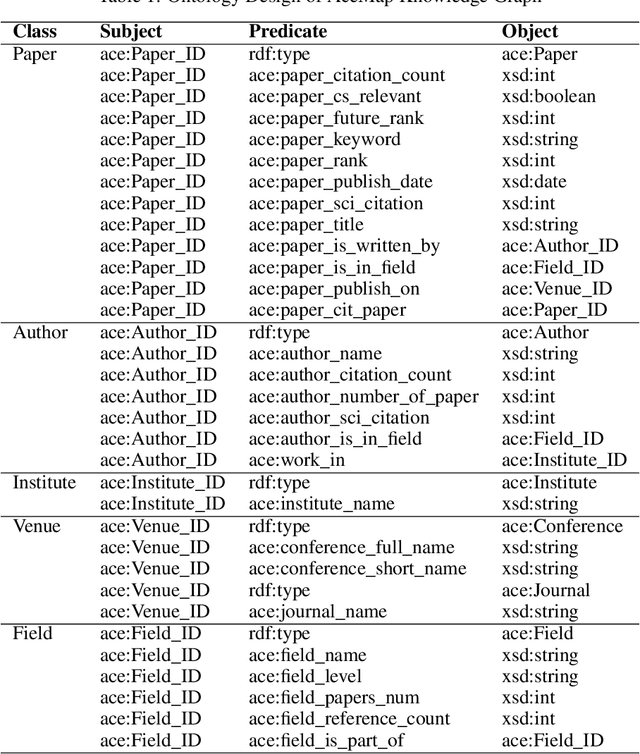
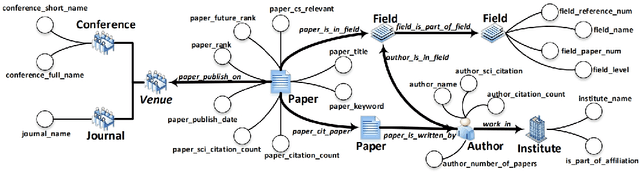
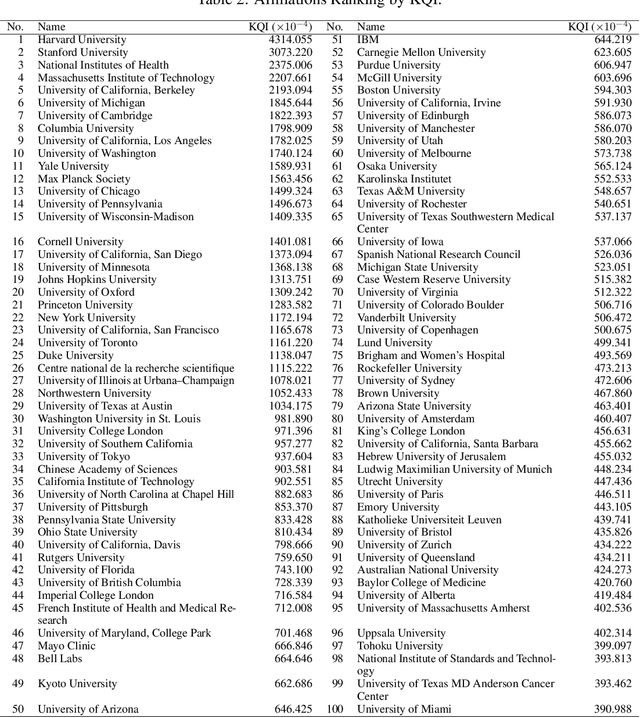
The exponential growth of scientific literature requires effective management and extraction of valuable insights. While existing scientific search engines excel at delivering search results based on relational databases, they often neglect the analysis of collaborations between scientific entities and the evolution of ideas, as well as the in-depth analysis of content within scientific publications. The representation of heterogeneous graphs and the effective measurement, analysis, and mining of such graphs pose significant challenges. To address these challenges, we present AceMap, an academic system designed for knowledge discovery through academic graph. We present advanced database construction techniques to build the comprehensive AceMap database with large-scale academic publications that contain rich visual, textual, and numerical information. AceMap also employs innovative visualization, quantification, and analysis methods to explore associations and logical relationships among academic entities. AceMap introduces large-scale academic network visualization techniques centered on nebular graphs, providing a comprehensive view of academic networks from multiple perspectives. In addition, AceMap proposes a unified metric based on structural entropy to quantitatively measure the knowledge content of different academic entities. Moreover, AceMap provides advanced analysis capabilities, including tracing the evolution of academic ideas through citation relationships and concept co-occurrence, and generating concise summaries informed by this evolutionary process. In addition, AceMap uses machine reading methods to generate potential new ideas at the intersection of different fields. Exploring the integration of large language models and knowledge graphs is a promising direction for future research in idea evolution. Please visit \url{https://www.acemap.info} for further exploration.

On Geometric Structure of Activation Spaces in Neural Networks

In this paper, we investigate the geometric structure of activation spaces of fully connected layers in neural networks and then show applications of this study. We propose an efficient approximation algorithm to characterize the convex hull of massive points in high dimensional space. Based on this new algorithm, four common geometric properties shared by the activation spaces are concluded, which gives a rather clear description of the activation spaces. We then propose an alternative classification method grounding on the geometric structure description, which works better than neural networks alone. Surprisingly, this data classification method can be an indicator of overfitting in neural networks. We believe our work reveals several critical intrinsic properties of modern neural networks and further gives a new metric for evaluating them.