Advancing Generalization in PINNs through Latent-Space Representations

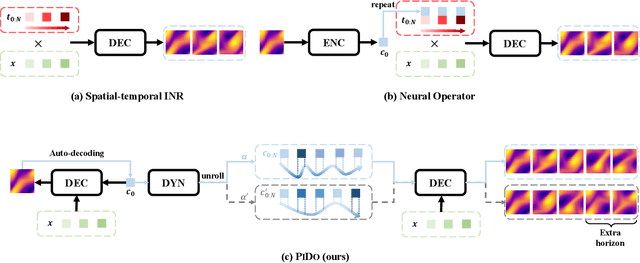
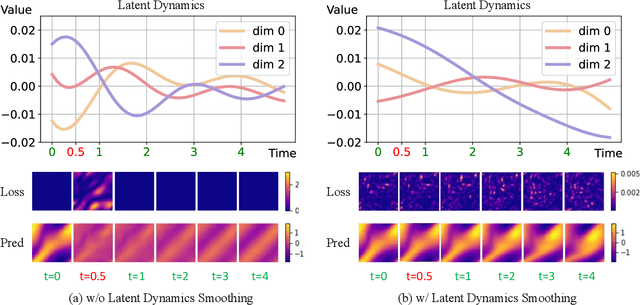
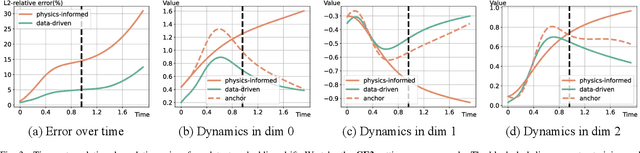
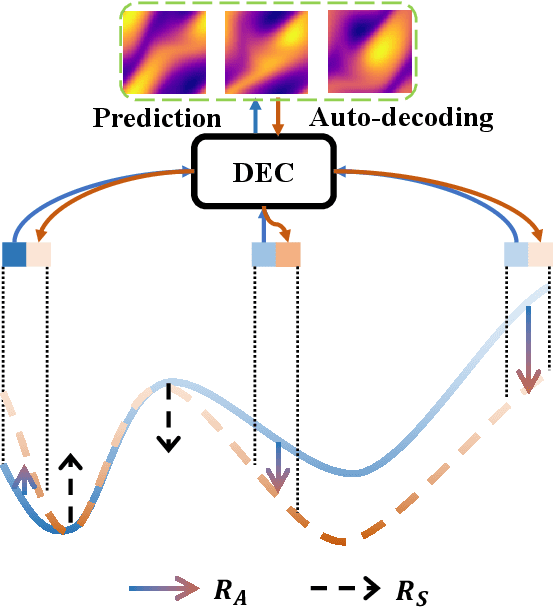
Physics-informed neural networks (PINNs) have made significant strides in modeling dynamical systems governed by partial differential equations (PDEs). However, their generalization capabilities across varying scenarios remain limited. To overcome this limitation, we propose PIDO, a novel physics-informed neural PDE solver designed to generalize effectively across diverse PDE configurations, including varying initial conditions, PDE coefficients, and training time horizons. PIDO exploits the shared underlying structure of dynamical systems with different properties by projecting PDE solutions into a latent space using auto-decoding. It then learns the dynamics of these latent representations, conditioned on the PDE coefficients. Despite its promise, integrating latent dynamics models within a physics-informed framework poses challenges due to the optimization difficulties associated with physics-informed losses. To address these challenges, we introduce a novel approach that diagnoses and mitigates these issues within the latent space. This strategy employs straightforward yet effective regularization techniques, enhancing both the temporal extrapolation performance and the training stability of PIDO. We validate PIDO on a range of benchmarks, including 1D combined equations and 2D Navier-Stokes equations. Additionally, we demonstrate the transferability of its learned representations to downstream applications such as long-term integration and inverse problems.

Pedestrian Trajectory Prediction Using Dynamics-based Deep Learning

Pedestrian trajectory prediction plays an important role in autonomous driving systems and robotics. Recent work utilising prominent deep learning models for pedestrian motion prediction makes limited a priori assumptions about human movements, resulting in a lack of explainability and explicit constraints enforced on predicted trajectories. This paper presents a dynamics-based deep learning framework where a novel asymptotically stable dynamical system is integrated into a deep learning model. Our novel asymptotically stable dynamical system is used to model human goal-targeted motion by enforcing the human walking trajectory converges to a predicted goal position and provides a deep learning model with prior knowledge and explainability. Our deep learning model utilises recent innovations from transformer networks and is used to learn some features of human motion, such as collision avoidance, for our proposed dynamical system. The experimental results show that our framework outperforms recent prominent models in pedestrian trajectory prediction on five benchmark human motion datasets.

Learning Specialized Activation Functions for Physics-informed Neural Networks

Physics-informed neural networks (PINNs) are known to suffer from optimization difficulty. In this work, we reveal the connection between the optimization difficulty of PINNs and activation functions. Specifically, we show that PINNs exhibit high sensitivity to activation functions when solving PDEs with distinct properties. Existing works usually choose activation functions by inefficient trial-and-error. To avoid the inefficient manual selection and to alleviate the optimization difficulty of PINNs, we introduce adaptive activation functions to search for the optimal function when solving different problems. We compare different adaptive activation functions and discuss their limitations in the context of PINNs. Furthermore, we propose to tailor the idea of learning combinations of candidate activation functions to the PINNs optimization, which has a higher requirement for the smoothness and diversity on learned functions. This is achieved by removing activation functions which cannot provide higher-order derivatives from the candidate set and incorporating elementary functions with different properties according to our prior knowledge about the PDE at hand. We further enhance the search space with adaptive slopes. The proposed adaptive activation function can be used to solve different PDE systems in an interpretable way. Its effectiveness is demonstrated on a series of benchmarks. Code is available at https://github.com/LeapLabTHU/AdaAFforPINNs.

Exploring the Equivalence of Siamese Self-Supervised Learning via A Unified Gradient Framework

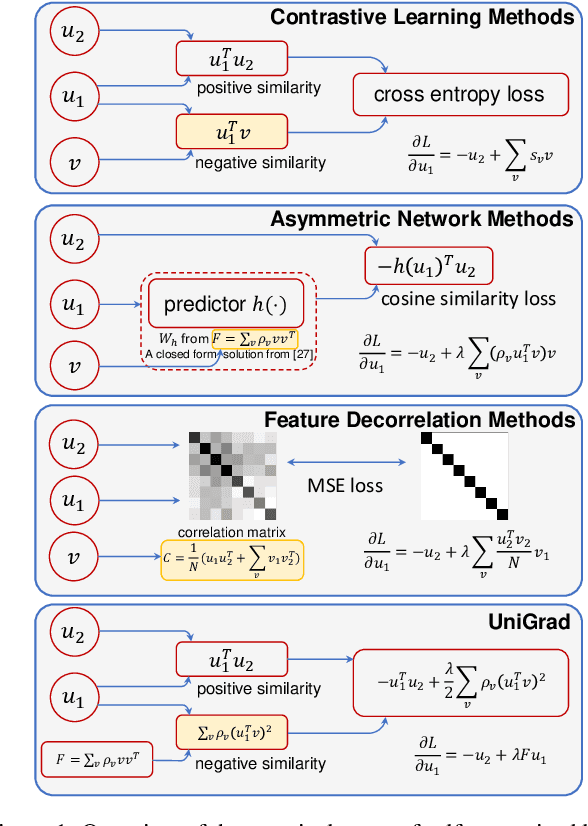
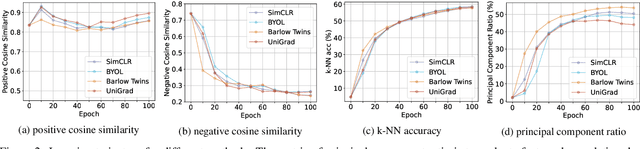
Self-supervised learning has shown its great potential to extract powerful visual representations without human annotations. Various works are proposed to deal with self-supervised learning from different perspectives: (1) contrastive learning methods (e.g., MoCo, SimCLR) utilize both positive and negative samples to guide the training direction; (2) asymmetric network methods (e.g., BYOL, SimSiam) get rid of negative samples via the introduction of a predictor network and the stop-gradient operation; (3) feature decorrelation methods (e.g., Barlow Twins, VICReg) instead aim to reduce the redundancy between feature dimensions. These methods appear to be quite different in the designed loss functions from various motivations. The final accuracy numbers also vary, where different networks and tricks are utilized in different works. In this work, we demonstrate that these methods can be unified into the same form. Instead of comparing their loss functions, we derive a unified formula through gradient analysis. Furthermore, we conduct fair and detailed experiments to compare their performances. It turns out that there is little gap between these methods, and the use of momentum encoder is the key factor to boost performance. From this unified framework, we propose UniGrad, a simple but effective gradient form for self-supervised learning. It does not require a memory bank or a predictor network, but can still achieve state-of-the-art performance and easily adopt other training strategies. Extensive experiments on linear evaluation and many downstream tasks also show its effectiveness. Code shall be released.

Dynamic Neural Networks: A Survey

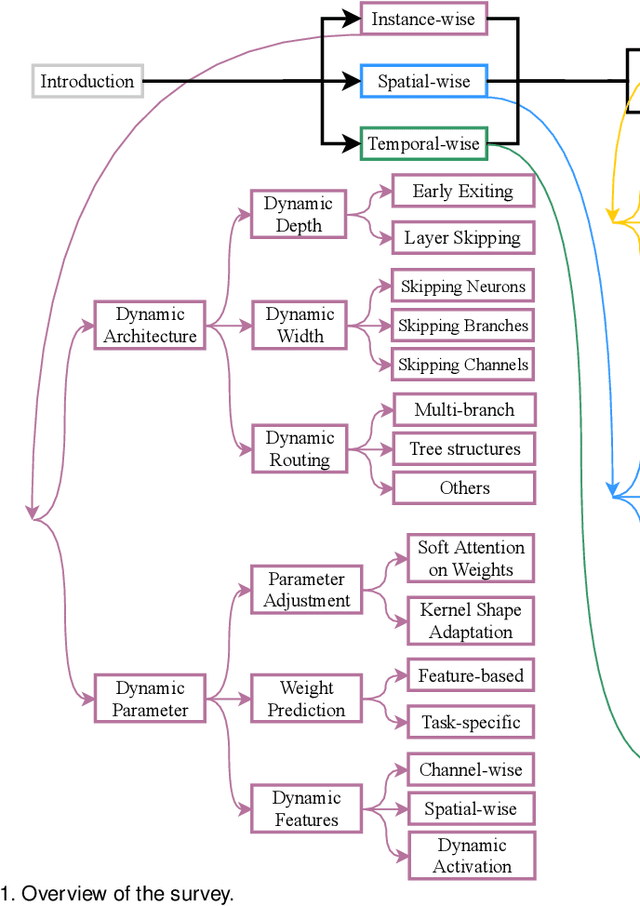
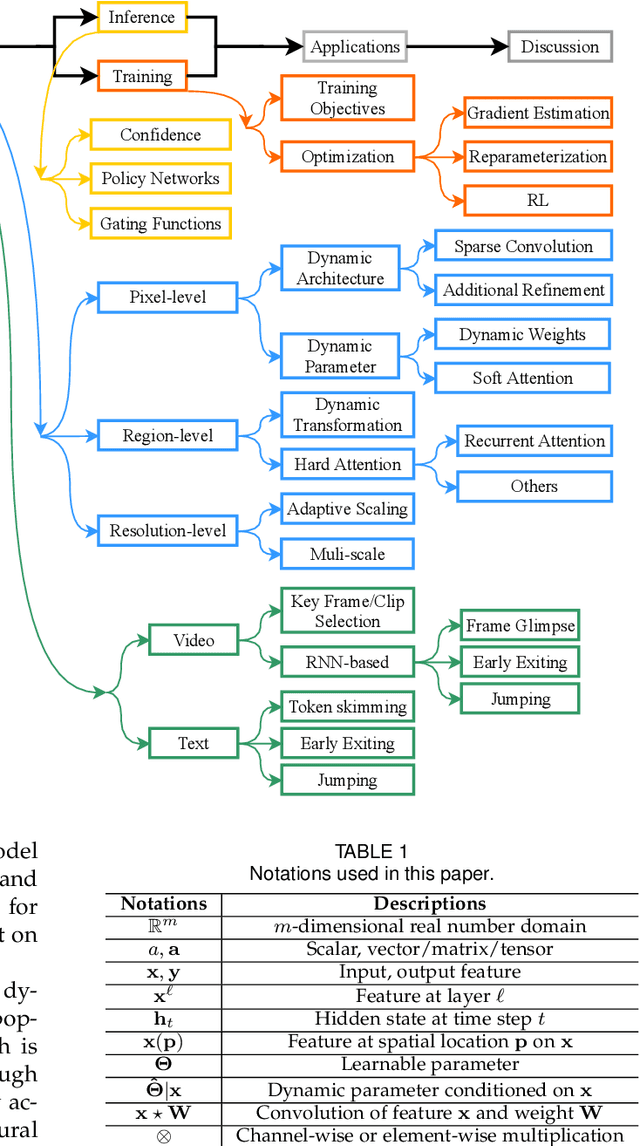
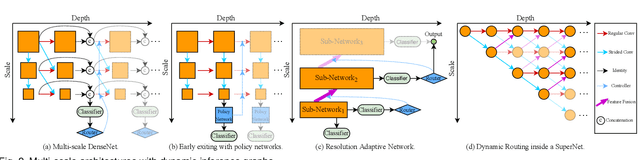
Dynamic neural network is an emerging research topic in deep learning. Compared to static models which have fixed computational graphs and parameters at the inference stage, dynamic networks can adapt their structures or parameters to different inputs, leading to notable advantages in terms of accuracy, computational efficiency, adaptiveness, etc. In this survey, we comprehensively review this rapidly developing area by dividing dynamic networks into three main categories: 1) instance-wise dynamic models that process each instance with data-dependent architectures or parameters; 2) spatial-wise dynamic networks that conduct adaptive computation with respect to different spatial locations of image data and 3) temporal-wise dynamic models that perform adaptive inference along the temporal dimension for sequential data such as videos and texts. The important research problems of dynamic networks, e.g., architecture design, decision making scheme, optimization technique and applications, are reviewed systematically. Finally, we discuss the open problems in this field together with interesting future research directions.