Advancing Generalization in PINNs through Latent-Space Representations
Paper and Code
Nov 28, 2024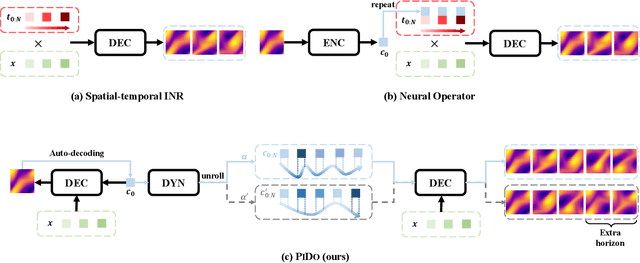
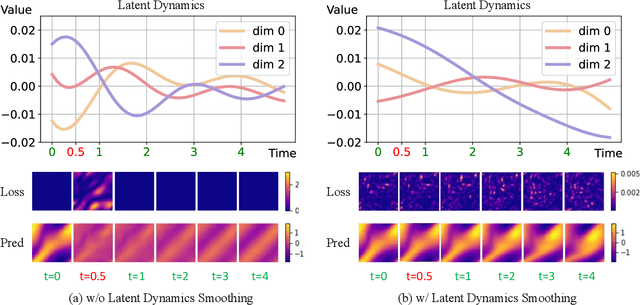
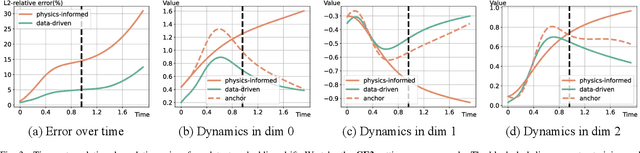
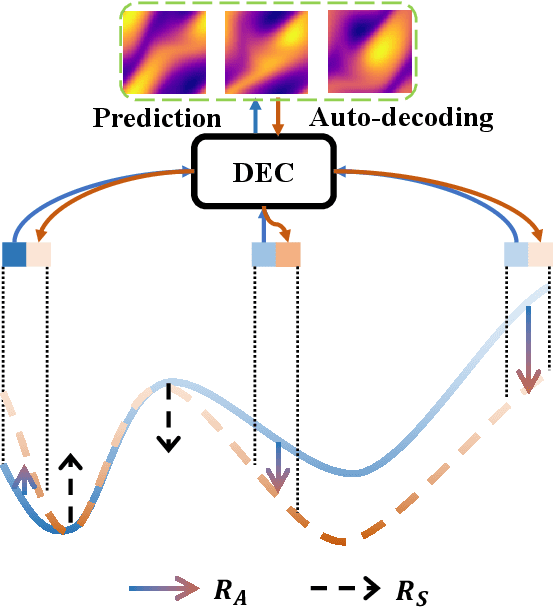
Physics-informed neural networks (PINNs) have made significant strides in modeling dynamical systems governed by partial differential equations (PDEs). However, their generalization capabilities across varying scenarios remain limited. To overcome this limitation, we propose PIDO, a novel physics-informed neural PDE solver designed to generalize effectively across diverse PDE configurations, including varying initial conditions, PDE coefficients, and training time horizons. PIDO exploits the shared underlying structure of dynamical systems with different properties by projecting PDE solutions into a latent space using auto-decoding. It then learns the dynamics of these latent representations, conditioned on the PDE coefficients. Despite its promise, integrating latent dynamics models within a physics-informed framework poses challenges due to the optimization difficulties associated with physics-informed losses. To address these challenges, we introduce a novel approach that diagnoses and mitigates these issues within the latent space. This strategy employs straightforward yet effective regularization techniques, enhancing both the temporal extrapolation performance and the training stability of PIDO. We validate PIDO on a range of benchmarks, including 1D combined equations and 2D Navier-Stokes equations. Additionally, we demonstrate the transferability of its learned representations to downstream applications such as long-term integration and inverse problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge