Hongchang Gao
Federated Stochastic Minimax Optimization under Heavy-Tailed Noises
Nov 06, 2025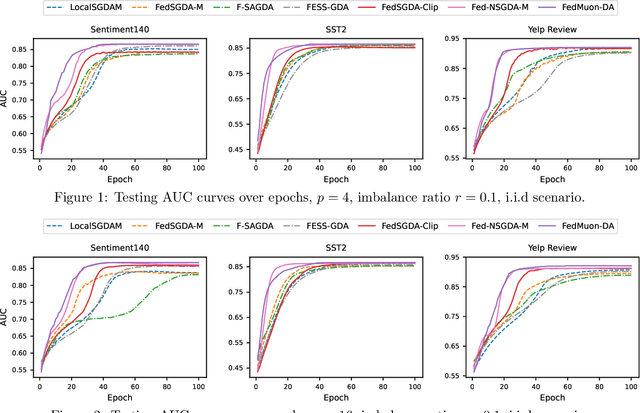
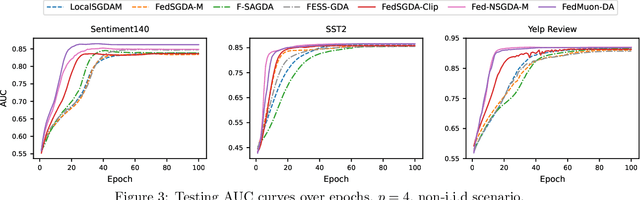
Abstract:Heavy-tailed noise has attracted growing attention in nonconvex stochastic optimization, as numerous empirical studies suggest it offers a more realistic assumption than standard bounded variance assumption. In this work, we investigate nonconvex-PL minimax optimization under heavy-tailed gradient noise in federated learning. We propose two novel algorithms: Fed-NSGDA-M, which integrates normalized gradients, and FedMuon-DA, which leverages the Muon optimizer for local updates. Both algorithms are designed to effectively address heavy-tailed noise in federated minimax optimization, under a milder condition. We theoretically establish that both algorithms achieve a convergence rate of $O({1}/{(TNp)^{\frac{s-1}{2s}}})$. To the best of our knowledge, these are the first federated minimax optimization algorithms with rigorous theoretical guarantees under heavy-tailed noise. Extensive experiments further validate their effectiveness.
Nonconvex Decentralized Stochastic Bilevel Optimization under Heavy-Tailed Noises
Sep 19, 2025Abstract:Existing decentralized stochastic optimization methods assume the lower-level loss function is strongly convex and the stochastic gradient noise has finite variance. These strong assumptions typically are not satisfied in real-world machine learning models. To address these limitations, we develop a novel decentralized stochastic bilevel optimization algorithm for the nonconvex bilevel optimization problem under heavy-tailed noises. Specifically, we develop a normalized stochastic variance-reduced bilevel gradient descent algorithm, which does not rely on any clipping operation. Moreover, we establish its convergence rate by innovatively bounding interdependent gradient sequences under heavy-tailed noises for nonconvex decentralized bilevel optimization problems. As far as we know, this is the first decentralized bilevel optimization algorithm with rigorous theoretical guarantees under heavy-tailed noises. The extensive experimental results confirm the effectiveness of our algorithm in handling heavy-tailed noises.
Gradient-Free Method for Heavily Constrained Nonconvex Optimization
Aug 31, 2024



Abstract:Zeroth-order (ZO) method has been shown to be a powerful method for solving the optimization problem where explicit expression of the gradients is difficult or infeasible to obtain. Recently, due to the practical value of the constrained problems, a lot of ZO Frank-Wolfe or projected ZO methods have been proposed. However, in many applications, we may have a very large number of nonconvex white/black-box constraints, which makes the existing zeroth-order methods extremely inefficient (or even not working) since they need to inquire function value of all the constraints and project the solution to the complicated feasible set. In this paper, to solve the nonconvex problem with a large number of white/black-box constraints, we proposed a doubly stochastic zeroth-order gradient method (DSZOG) with momentum method and adaptive step size. Theoretically, we prove DSZOG can converge to the $\epsilon$-stationary point of the constrained problem. Experimental results in two applications demonstrate the superiority of our method in terms of training time and accuracy compared with other ZO methods for the constrained problem.
* 21 page, 12 figures, conference
AMOSL: Adaptive Modality-wise Structure Learning in Multi-view Graph Neural Networks For Enhanced Unified Representation
Jun 04, 2024Abstract:While Multi-view Graph Neural Networks (MVGNNs) excel at leveraging diverse modalities for learning object representation, existing methods assume identical local topology structures across modalities that overlook real-world discrepancies. This leads MVGNNs straggles in modality fusion and representations denoising. To address these issues, we propose adaptive modality-wise structure learning (AMoSL). AMoSL captures node correspondences between modalities via optimal transport, and jointly learning with graph embedding. To enable efficient end-to-end training, we employ an efficient solution for the resulting complex bilevel optimization problem. Furthermore, AMoSL adapts to downstream tasks through unsupervised learning on inter-modality distances. The effectiveness of AMoSL is demonstrated by its ability to train more accurate graph classifiers on six benchmark datasets.
On the Communication Complexity of Decentralized Bilevel Optimization
Nov 19, 2023



Abstract:Decentralized bilevel optimization has been actively studied in the past few years since it has widespread applications in machine learning. However, existing algorithms suffer from large communication complexity caused by the estimation of stochastic hypergradient, limiting their application to real-world tasks. To address this issue, we develop a novel decentralized stochastic bilevel gradient descent algorithm under the heterogeneous setting, which enjoys a small communication cost in each round and small communication rounds. As such, it can achieve a much better communication complexity than existing algorithms. Moreover, we extend our algorithm to the more challenging decentralized multi-level optimization. To the best of our knowledge, this is the first time achieving these theoretical results under the heterogeneous setting. At last, the experimental results confirm the efficacy of our algorithm.
Achieving Linear Speedup in Decentralized Stochastic Compositional Minimax Optimization
Aug 01, 2023Abstract:The stochastic compositional minimax problem has attracted a surge of attention in recent years since it covers many emerging machine learning models. Meanwhile, due to the emergence of distributed data, optimizing this kind of problem under the decentralized setting becomes badly needed. However, the compositional structure in the loss function brings unique challenges to designing efficient decentralized optimization algorithms. In particular, our study shows that the standard gossip communication strategy cannot achieve linear speedup for decentralized compositional minimax problems due to the large consensus error about the inner-level function. To address this issue, we developed a novel decentralized stochastic compositional gradient descent ascent with momentum algorithm to reduce the consensus error in the inner-level function. As such, our theoretical results demonstrate that it is able to achieve linear speedup with respect to the number of workers. We believe this novel algorithmic design could benefit the development of decentralized compositional optimization. Finally, we applied our methods to the imbalanced classification problem. The extensive experimental results provide evidence for the effectiveness of our algorithm.
Set-level Guidance Attack: Boosting Adversarial Transferability of Vision-Language Pre-training Models
Jul 26, 2023Abstract:Vision-language pre-training (VLP) models have shown vulnerability to adversarial examples in multimodal tasks. Furthermore, malicious adversaries can be deliberately transferred to attack other black-box models. However, existing work has mainly focused on investigating white-box attacks. In this paper, we present the first study to investigate the adversarial transferability of recent VLP models. We observe that existing methods exhibit much lower transferability, compared to the strong attack performance in white-box settings. The transferability degradation is partly caused by the under-utilization of cross-modal interactions. Particularly, unlike unimodal learning, VLP models rely heavily on cross-modal interactions and the multimodal alignments are many-to-many, e.g., an image can be described in various natural languages. To this end, we propose a highly transferable Set-level Guidance Attack (SGA) that thoroughly leverages modality interactions and incorporates alignment-preserving augmentation with cross-modal guidance. Experimental results demonstrate that SGA could generate adversarial examples that can strongly transfer across different VLP models on multiple downstream vision-language tasks. On image-text retrieval, SGA significantly enhances the attack success rate for transfer attacks from ALBEF to TCL by a large margin (at least 9.78% and up to 30.21%), compared to the state-of-the-art.
Stochastic Multi-Level Compositional Optimization Algorithms over Networks with Level-Independent Convergence Rate
Jun 06, 2023Abstract:Stochastic multi-level compositional optimization problems cover many new machine learning paradigms, e.g., multi-step model-agnostic meta-learning, which require efficient optimization algorithms for large-scale applications. This paper studies the decentralized stochastic multi-level optimization algorithm, which is challenging because the multi-level structure and decentralized communication scheme may make the number of levels affect the order of the convergence rate. To this end, we develop two novel decentralized optimization algorithms to deal with the multi-level function and its gradient. Our theoretical results show that both algorithms can achieve the level-independent convergence rate for nonconvex problems under much milder conditions compared with existing single-machine algorithms. To the best of our knowledge, this is the first work that achieves the level-independent convergence rate under the decentralized setting. Moreover, extensive experiments confirm the efficacy of our proposed algorithms.
When Decentralized Optimization Meets Federated Learning
Jun 05, 2023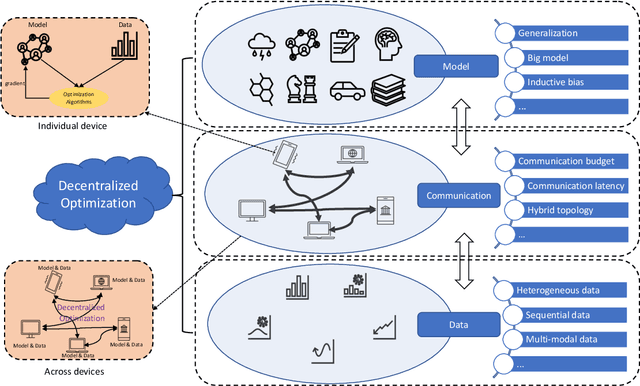
Abstract:Federated learning is a new learning paradigm for extracting knowledge from distributed data. Due to its favorable properties in preserving privacy and saving communication costs, it has been extensively studied and widely applied to numerous data analysis applications. However, most existing federated learning approaches concentrate on the centralized setting, which is vulnerable to a single-point failure. An alternative strategy for addressing this issue is the decentralized communication topology. In this article, we systematically investigate the challenges and opportunities when renovating decentralized optimization for federated learning. In particular, we discussed them from the model, data, and communication sides, respectively, which can deepen our understanding about decentralized federated learning.
Can Decentralized Stochastic Minimax Optimization Algorithms Converge Linearly for Finite-Sum Nonconvex-Nonconcave Problems?
Apr 24, 2023Abstract:Decentralized minimax optimization has been actively studied in the past few years due to its application in a wide range of machine learning models. However, the current theoretical understanding of its convergence rate is far from satisfactory since existing works only focus on the nonconvex-strongly-concave problem. This motivates us to study decentralized minimax optimization algorithms for the nonconvex-nonconcave problem. To this end, we develop two novel decentralized stochastic variance-reduced gradient descent ascent algorithms for the finite-sum nonconvex-nonconcave problem that satisfies the Polyak-{\L}ojasiewicz (PL) condition. In particular, our theoretical analyses demonstrate how to conduct local updates and perform communication to achieve the linear convergence rate. To the best of our knowledge, this is the first work achieving linear convergence rates for decentralized nonconvex-nonconcave problems. Finally, we verify the performance of our algorithms on both synthetic and real-world datasets. The experimental results confirm the efficacy of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge