Interaction-via-Actions: Cattle Interaction Detection with Joint Learning of Action-Interaction Latent Space

This paper introduces a method and application for automatically detecting behavioral interactions between grazing cattle from a single image, which is essential for smart livestock management in the cattle industry, such as for detecting estrus. Although interaction detection for humans has been actively studied, a non-trivial challenge lies in cattle interaction detection, specifically the lack of a comprehensive behavioral dataset that includes interactions, as the interactions of grazing cattle are rare events. We, therefore, propose CattleAct, a data-efficient method for interaction detection by decomposing interactions into the combinations of actions by individual cattle. Specifically, we first learn an action latent space from a large-scale cattle action dataset. Then, we embed rare interactions via the fine-tuning of the pre-trained latent space using contrastive learning, thereby constructing a unified latent space of actions and interactions. On top of the proposed method, we develop a practical working system integrating video and GPS inputs. Experiments on a commercial-scale pasture demonstrate the accurate interaction detection achieved by our method compared to the baselines. Our implementation is available at https://github.com/rakawanegan/CattleAct.

GaussianPlant: Structure-aligned Gaussian Splatting for 3D Reconstruction of Plants

We present a method for jointly recovering the appearance and internal structure of botanical plants from multi-view images based on 3D Gaussian Splatting (3DGS). While 3DGS exhibits robust reconstruction of scene appearance for novel-view synthesis, it lacks structural representations underlying those appearances (e.g., branching patterns of plants), which limits its applicability to tasks such as plant phenotyping. To achieve both high-fidelity appearance and structural reconstruction, we introduce GaussianPlant, a hierarchical 3DGS representation, which disentangles structure and appearance. Specifically, we employ structure primitives (StPs) to explicitly represent branch and leaf geometry, and appearance primitives (ApPs) to the plants' appearance using 3D Gaussians. StPs represent a simplified structure of the plant, i.e., modeling branches as cylinders and leaves as disks. To accurately distinguish the branches and leaves, StP's attributes (i.e., branches or leaves) are optimized in a self-organized manner. ApPs are bound to each StP to represent the appearance of branches or leaves as in conventional 3DGS. StPs and ApPs are jointly optimized using a re-rendering loss on the input multi-view images, as well as the gradient flow from ApP to StP using the binding correspondence information. We conduct experiments to qualitatively evaluate the reconstruction accuracy of both appearance and structure, as well as real-world experiments to qualitatively validate the practical performance. Experiments show that the GaussianPlant achieves both high-fidelity appearance reconstruction via ApPs and accurate structural reconstruction via StPs, enabling the extraction of branch structure and leaf instances.

Zero-shot Hierarchical Plant Segmentation via Foundation Segmentation Models and Text-to-image Attention

Foundation segmentation models achieve reasonable leaf instance extraction from top-view crop images without training (i.e., zero-shot). However, segmenting entire plant individuals with each consisting of multiple overlapping leaves remains challenging. This problem is referred to as a hierarchical segmentation task, typically requiring annotated training datasets, which are often species-specific and require notable human labor. To address this, we introduce ZeroPlantSeg, a zero-shot segmentation for rosette-shaped plant individuals from top-view images. We integrate a foundation segmentation model, extracting leaf instances, and a vision-language model, reasoning about plants' structures to extract plant individuals without additional training. Evaluations on datasets with multiple plant species, growth stages, and shooting environments demonstrate that our method surpasses existing zero-shot methods and achieves better cross-domain performance than supervised methods. Implementations are available at https://github.com/JunhaoXing/ZeroPlantSeg.

Spectral Sensitivity Estimation with an Uncalibrated Diffraction Grating

This paper introduces a practical and accurate calibration method for camera spectral sensitivity using a diffraction grating. Accurate calibration of camera spectral sensitivity is crucial for various computer vision tasks, including color correction, illumination estimation, and material analysis. Unlike existing approaches that require specialized narrow-band filters or reference targets with known spectral reflectances, our method only requires an uncalibrated diffraction grating sheet, readily available off-the-shelf. By capturing images of the direct illumination and its diffracted pattern through the grating sheet, our method estimates both the camera spectral sensitivity and the diffraction grating parameters in a closed-form manner. Experiments on synthetic and real-world data demonstrate that our method outperforms conventional reference target-based methods, underscoring its effectiveness and practicality.

TreeFormer: Single-view Plant Skeleton Estimation via Tree-constrained Graph Generation

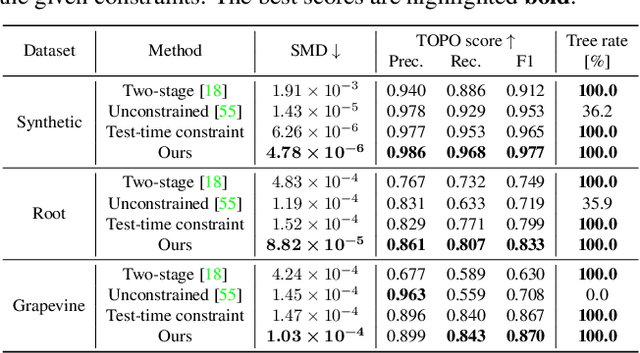
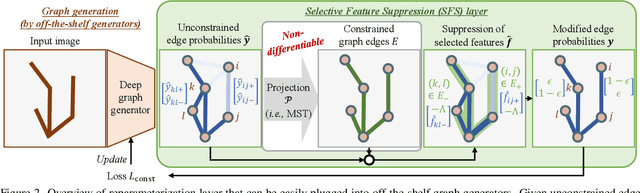
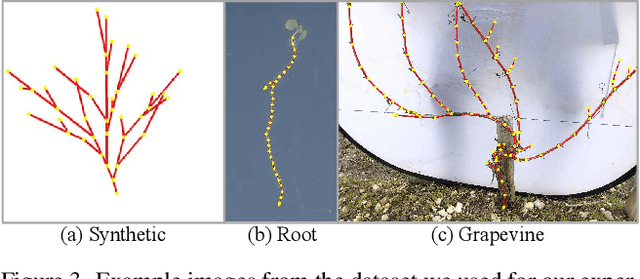
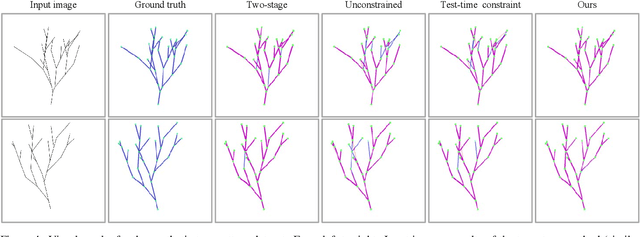
Accurate estimation of plant skeletal structure (e.g., branching structure) from images is essential for smart agriculture and plant science. Unlike human skeletons with fixed topology, plant skeleton estimation presents a unique challenge, i.e., estimating arbitrary tree graphs from images. While recent graph generation methods successfully infer thin structures from images, it is challenging to constrain the output graph strictly to a tree structure. To this problem, we present TreeFormer, a plant skeleton estimator via tree-constrained graph generation. Our approach combines learning-based graph generation with traditional graph algorithms to impose the constraints during the training loop. Specifically, our method projects an unconstrained graph onto a minimum spanning tree (MST) during the training loop and incorporates this prior knowledge into the gradient descent optimization by suppressing unwanted feature values. Experiments show that our method accurately estimates target plant skeletal structures for multiple domains: Synthetic tree patterns, real botanical roots, and grapevine branches. Our implementations are available at https://github.com/huntorochi/TreeFormer/.

NeRSP: Neural 3D Reconstruction for Reflective Objects with Sparse Polarized Images

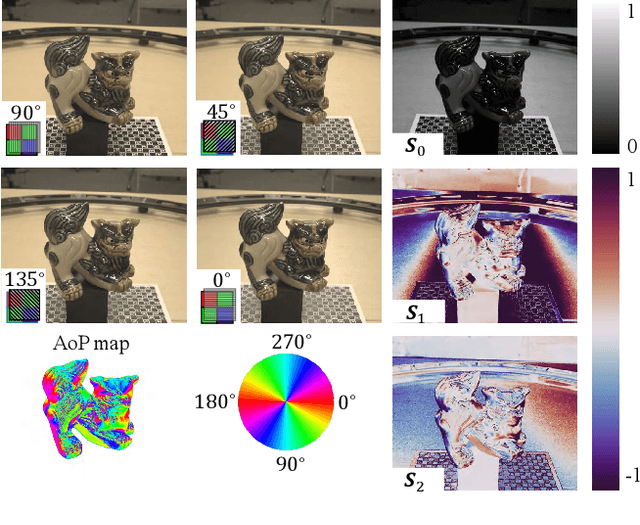
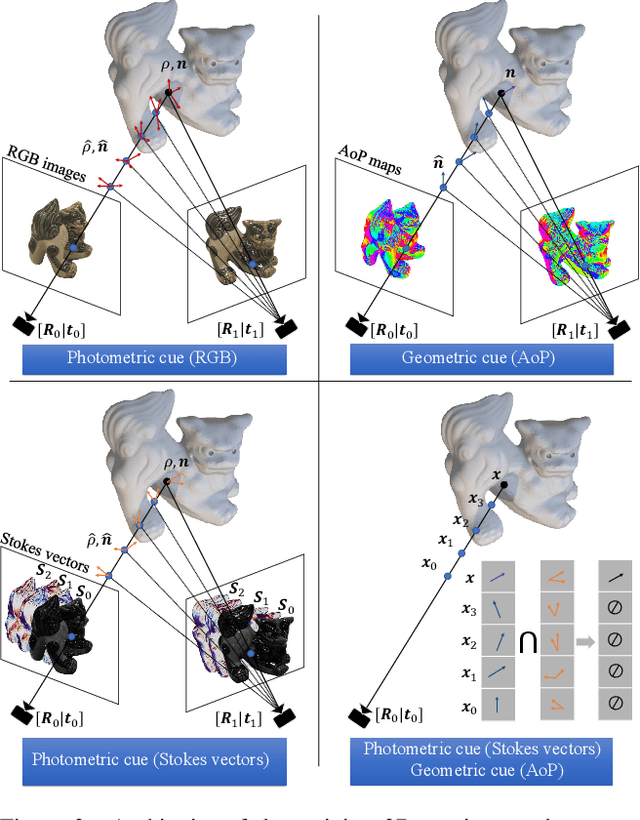
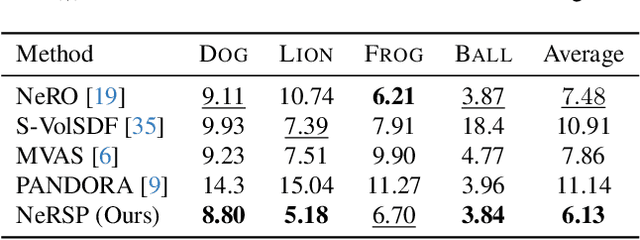
We present NeRSP, a Neural 3D reconstruction technique for Reflective surfaces with Sparse Polarized images. Reflective surface reconstruction is extremely challenging as specular reflections are view-dependent and thus violate the multiview consistency for multiview stereo. On the other hand, sparse image inputs, as a practical capture setting, commonly cause incomplete or distorted results due to the lack of correspondence matching. This paper jointly handles the challenges from sparse inputs and reflective surfaces by leveraging polarized images. We derive photometric and geometric cues from the polarimetric image formation model and multiview azimuth consistency, which jointly optimize the surface geometry modeled via implicit neural representation. Based on the experiments on our synthetic and real datasets, we achieve the state-of-the-art surface reconstruction results with only 6 views as input.

Multi-View Azimuth Stereo via Tangent Space Consistency

We present a method for 3D reconstruction only using calibrated multi-view surface azimuth maps. Our method, multi-view azimuth stereo, is effective for textureless or specular surfaces, which are difficult for conventional multi-view stereo methods. We introduce the concept of tangent space consistency: Multi-view azimuth observations of a surface point should be lifted to the same tangent space. Leveraging this consistency, we recover the shape by optimizing a neural implicit surface representation. Our method harnesses the robust azimuth estimation capabilities of photometric stereo methods or polarization imaging while bypassing potentially complex zenith angle estimation. Experiments using azimuth maps from various sources validate the accurate shape recovery with our method, even without zenith angles.

Edge-preserving Near-light Photometric Stereo with Neural Surfaces

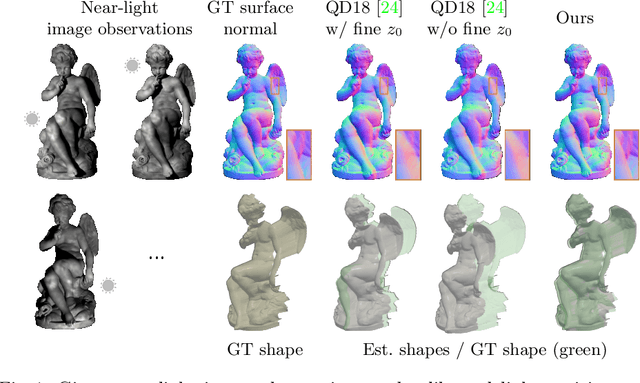
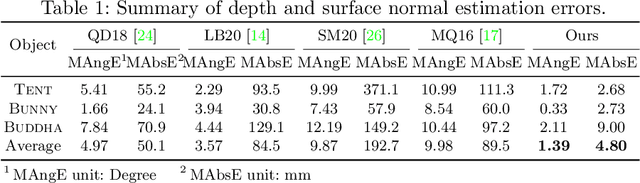
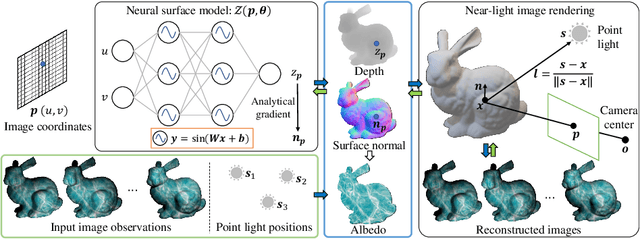
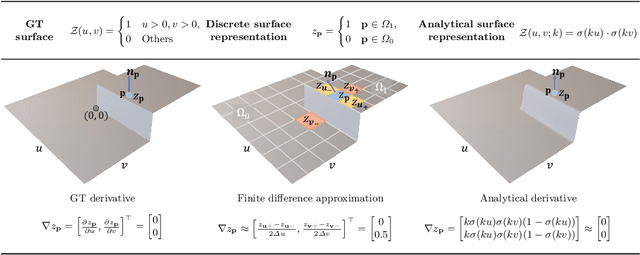
This paper presents a near-light photometric stereo method that faithfully preserves sharp depth edges in the 3D reconstruction. Unlike previous methods that rely on finite differentiation for approximating depth partial derivatives and surface normals, we introduce an analytically differentiable neural surface in near-light photometric stereo for avoiding differentiation errors at sharp depth edges, where the depth is represented as a neural function of the image coordinates. By further formulating the Lambertian albedo as a dependent variable resulting from the surface normal and depth, our method is insusceptible to inaccurate depth initialization. Experiments on both synthetic and real-world scenes demonstrate the effectiveness of our method for detailed shape recovery with edge preservation.