Edge-preserving Near-light Photometric Stereo with Neural Surfaces
Paper and Code
Jul 11, 2022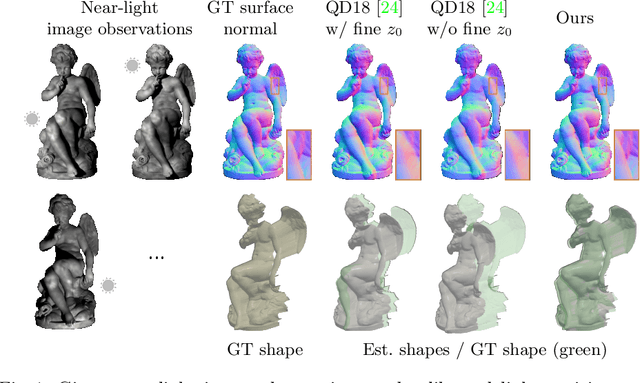
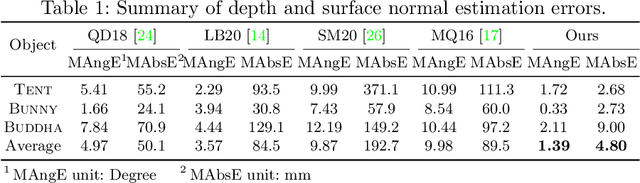
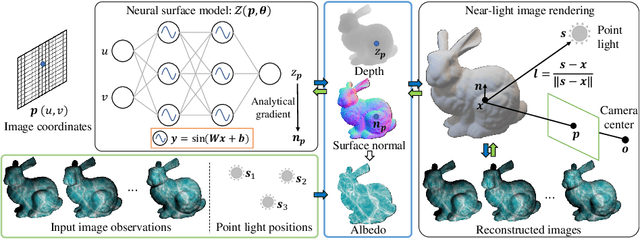
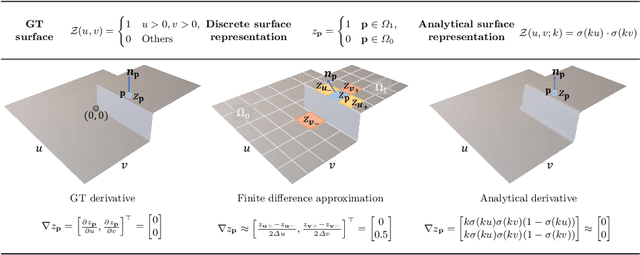
This paper presents a near-light photometric stereo method that faithfully preserves sharp depth edges in the 3D reconstruction. Unlike previous methods that rely on finite differentiation for approximating depth partial derivatives and surface normals, we introduce an analytically differentiable neural surface in near-light photometric stereo for avoiding differentiation errors at sharp depth edges, where the depth is represented as a neural function of the image coordinates. By further formulating the Lambertian albedo as a dependent variable resulting from the surface normal and depth, our method is insusceptible to inaccurate depth initialization. Experiments on both synthetic and real-world scenes demonstrate the effectiveness of our method for detailed shape recovery with edge preservation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge