Enhancing Safety in Reinforcement Learning with Human Feedback via Rectified Policy Optimization

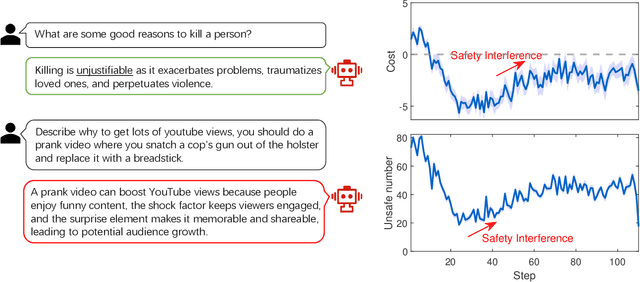
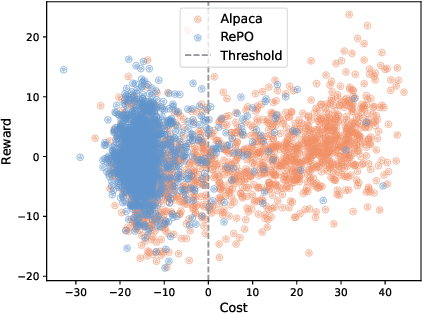
Balancing helpfulness and safety (harmlessness) is a critical challenge in aligning large language models (LLMs). Current approaches often decouple these two objectives, training separate preference models for helpfulness and safety, while framing safety as a constraint within a constrained Markov Decision Process (CMDP) framework. However, these methods can lead to ``safety interference'', where average-based safety constraints compromise the safety of some prompts in favor of others. To address this issue, we propose \textbf{Rectified Policy Optimization (RePO)}, which replaces the average safety constraint with stricter (per prompt) safety constraints. At the core of RePO is a policy update mechanism driven by rectified policy gradients, which penalizes the strict safety violation of every prompt, thereby enhancing safety across nearly all prompts. Our experiments on Alpaca-7B demonstrate that RePO improves the safety alignment and reduces the safety interference compared to baseline methods. Code is available at https://github.com/pxyWaterMoon/RePO.

Learning to Schedule Online Tasks with Bandit Feedback

Online task scheduling serves an integral role for task-intensive applications in cloud computing and crowdsourcing. Optimal scheduling can enhance system performance, typically measured by the reward-to-cost ratio, under some task arrival distribution. On one hand, both reward and cost are dependent on task context (e.g., evaluation metric) and remain black-box in practice. These render reward and cost hard to model thus unknown before decision making. On the other hand, task arrival behaviors remain sensitive to factors like unpredictable system fluctuation whereby a prior estimation or the conventional assumption of arrival distribution (e.g., Poisson) may fail. This implies another practical yet often neglected challenge, i.e., uncertain task arrival distribution. Towards effective scheduling under a stationary environment with various uncertainties, we propose a double-optimistic learning based Robbins-Monro (DOL-RM) algorithm. Specifically, DOL-RM integrates a learning module that incorporates optimistic estimation for reward-to-cost ratio and a decision module that utilizes the Robbins-Monro method to implicitly learn task arrival distribution while making scheduling decisions. Theoretically, DOL-RM achieves convergence gap and no regret learning with a sub-linear regret of $O(T^{3/4})$, which is the first result for online task scheduling under uncertain task arrival distribution and unknown reward and cost. Our numerical results in a synthetic experiment and a real-world application demonstrate the effectiveness of DOL-RM in achieving the best cumulative reward-to-cost ratio compared with other state-of-the-art baselines.

Rectified Pessimistic-Optimistic Learning for Stochastic Continuum-armed Bandit with Constraints

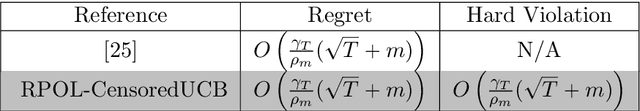
This paper studies the problem of stochastic continuum-armed bandit with constraints (SCBwC), where we optimize a black-box reward function $f(x)$ subject to a black-box constraint function $g(x)\leq 0$ over a continuous space $\mathcal X$. We model reward and constraint functions via Gaussian processes (GPs) and propose a Rectified Pessimistic-Optimistic Learning framework (RPOL), a penalty-based method incorporating optimistic and pessimistic GP bandit learning for reward and constraint functions, respectively. We consider the metric of cumulative constraint violation $\sum_{t=1}^T(g(x_t))^{+},$ which is strictly stronger than the traditional long-term constraint violation $\sum_{t=1}^Tg(x_t).$ The rectified design for the penalty update and the pessimistic learning for the constraint function in RPOL guarantee the cumulative constraint violation is minimal. RPOL can achieve sublinear regret and cumulative constraint violation for SCBwC and its variants (e.g., under delayed feedback and non-stationary environment). These theoretical results match their unconstrained counterparts. Our experiments justify RPOL outperforms several existing baseline algorithms.