Rectified Pessimistic-Optimistic Learning for Stochastic Continuum-armed Bandit with Constraints
Paper and Code
Nov 29, 2022

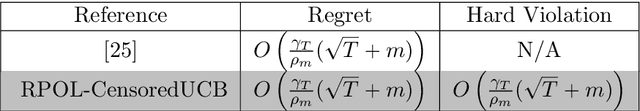

This paper studies the problem of stochastic continuum-armed bandit with constraints (SCBwC), where we optimize a black-box reward function $f(x)$ subject to a black-box constraint function $g(x)\leq 0$ over a continuous space $\mathcal X$. We model reward and constraint functions via Gaussian processes (GPs) and propose a Rectified Pessimistic-Optimistic Learning framework (RPOL), a penalty-based method incorporating optimistic and pessimistic GP bandit learning for reward and constraint functions, respectively. We consider the metric of cumulative constraint violation $\sum_{t=1}^T(g(x_t))^{+},$ which is strictly stronger than the traditional long-term constraint violation $\sum_{t=1}^Tg(x_t).$ The rectified design for the penalty update and the pessimistic learning for the constraint function in RPOL guarantee the cumulative constraint violation is minimal. RPOL can achieve sublinear regret and cumulative constraint violation for SCBwC and its variants (e.g., under delayed feedback and non-stationary environment). These theoretical results match their unconstrained counterparts. Our experiments justify RPOL outperforms several existing baseline algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge