Sparsity Inducing Representations for Policy Decompositions

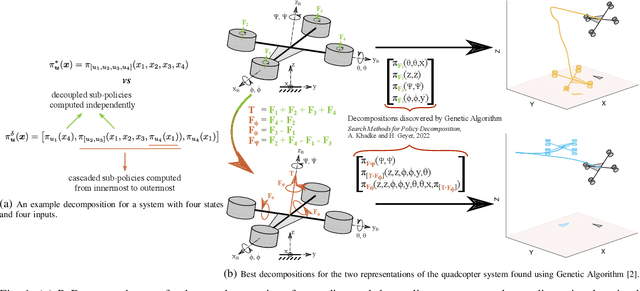
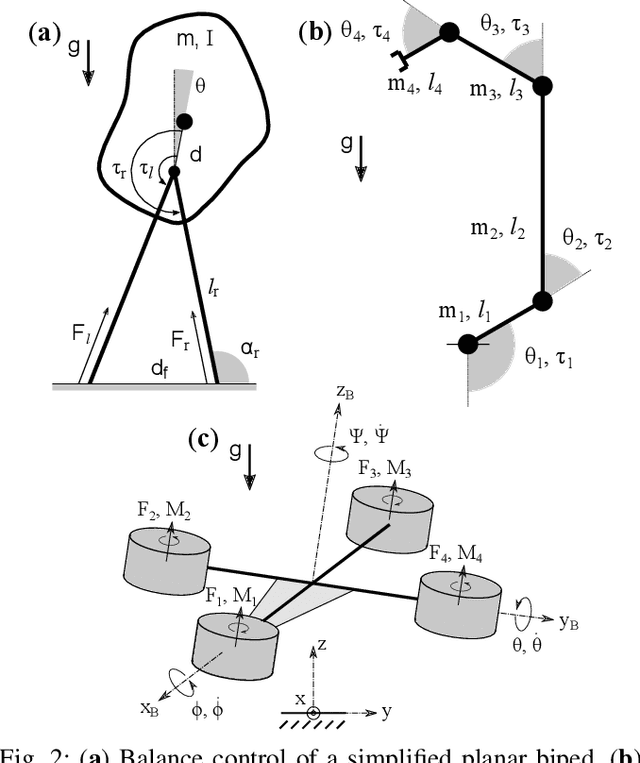
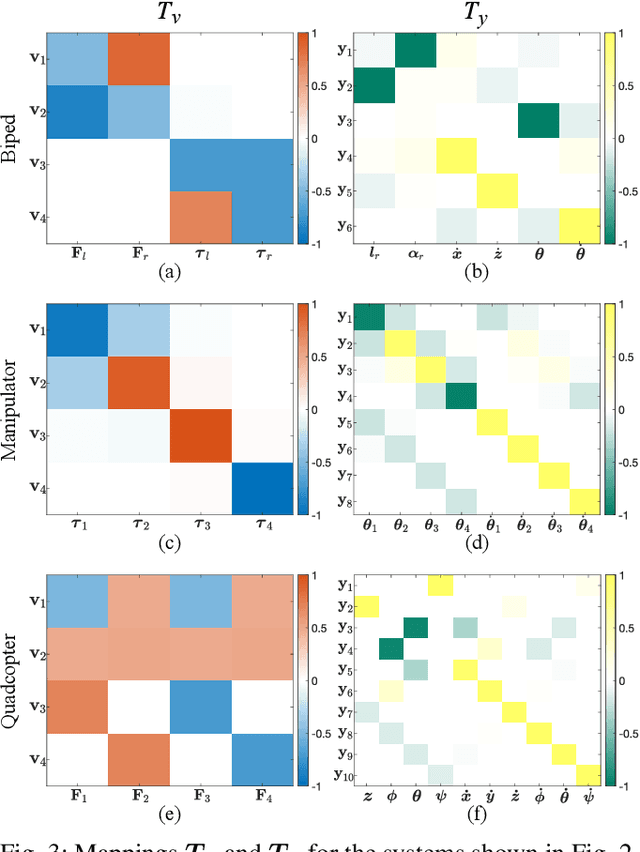
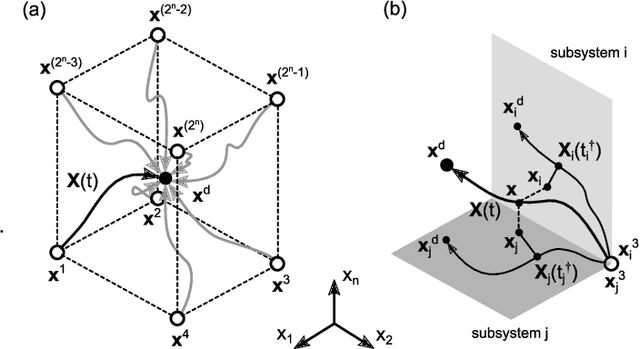
Policy Decomposition (PoDec) is a framework that lessens the curse of dimensionality when deriving policies to optimal control problems. For a given system representation, i.e. the state variables and control inputs describing a system, PoDec generates strategies to decompose the joint optimization of policies for all control inputs. Thereby, policies for different inputs are derived in a decoupled or cascaded fashion and as functions of some subsets of the state variables, leading to reduction in computation. However, the choice of system representation is crucial as it dictates the suboptimality of the resulting policies. We present a heuristic method to find a representation more amenable to decomposition. Our approach is based on the observation that every decomposition enforces a sparsity pattern in the resulting policies at the cost of optimality and a representation that already leads to a sparse optimal policy is likely to produce decompositions with lower suboptimalities. As the optimal policy is not known we construct a system representation that sparsifies its LQR approximation. For a simplified biped, a 4 degree-of-freedom manipulator, and a quadcopter, we discover decompositions that offer 10% reduction in trajectory costs over those identified by vanilla PoDec. Moreover, the decomposition policies produce trajectories with substantially lower costs compared to policies obtained from state-of-the-art reinforcement learning algorithms.

Search Methods for Policy Decompositions

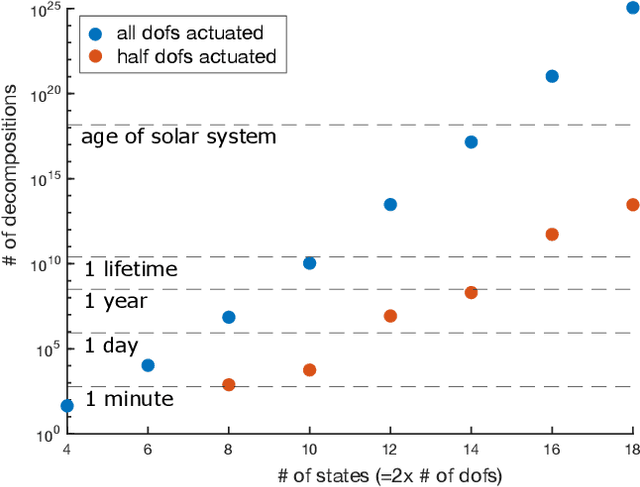
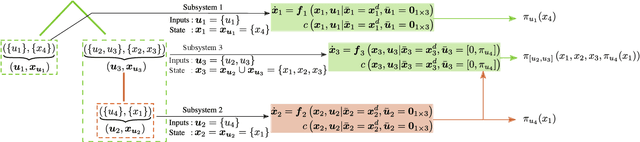
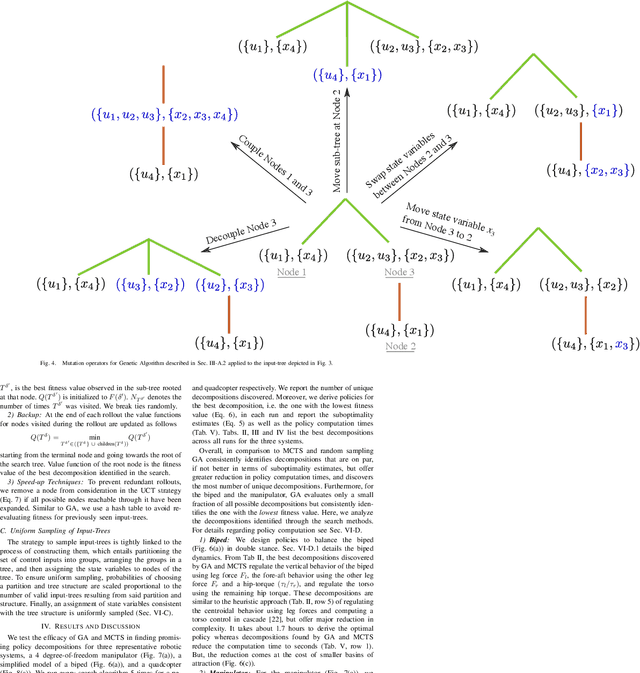
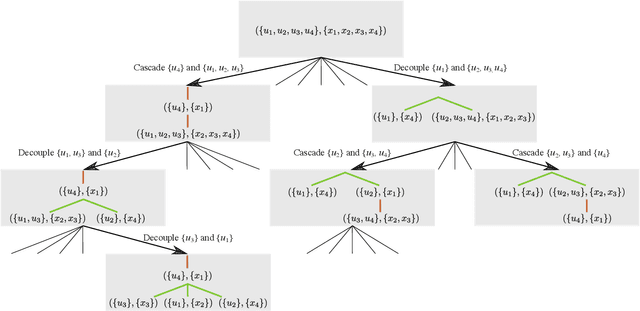
Computing optimal control policies for complex dynamical systems requires approximation methods to remain computationally tractable. Several approximation methods have been developed to tackle this problem. However, these methods do not reason about the suboptimality induced in the resulting control policies due to these approximations. We introduced Policy Decomposition, an approximation method that provides a suboptimality estimate, in our earlier work. Policy decomposition proposes strategies to break an optimal control problem into lower-dimensional subproblems, whose optimal solutions are combined to build a control policy for the original system. However, the number of possible strategies to decompose a system scale quickly with the complexity of a system, posing a combinatorial challenge. In this work we investigate the use of Genetic Algorithm and Monte-Carlo Tree Search to alleviate this challenge. We identify decompositions for swing-up control of a 4 degree-of-freedom manipulator, balance control of a simplified biped, and hover control of a quadcopter.

Policy Decomposition: Approximate Optimal Control with Suboptimality Estimates

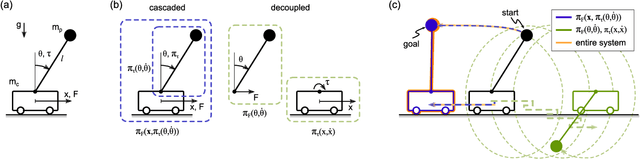
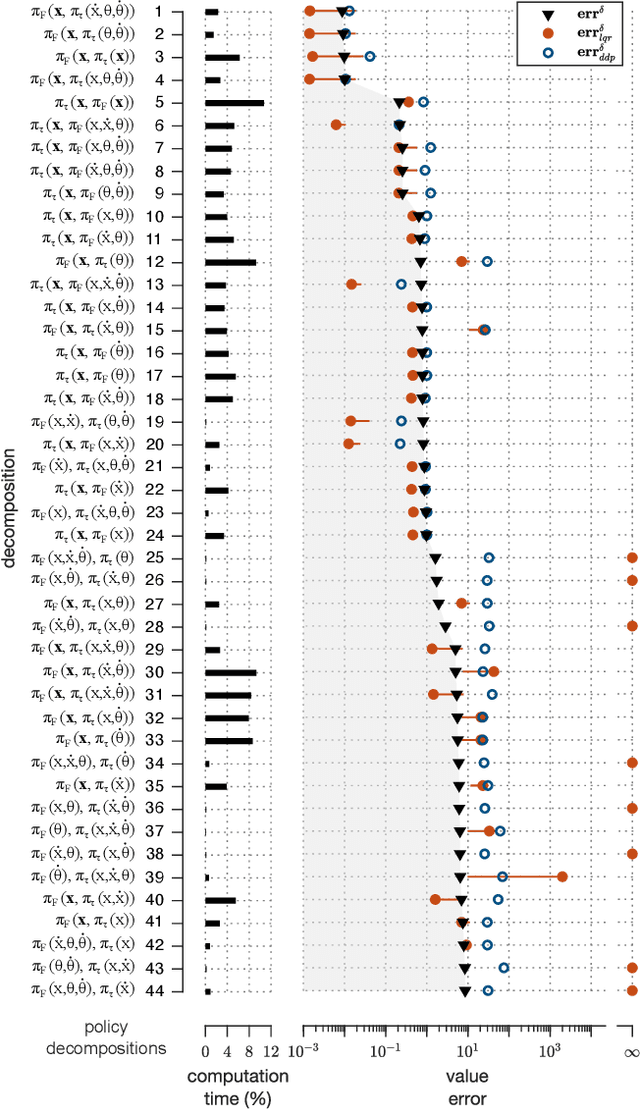
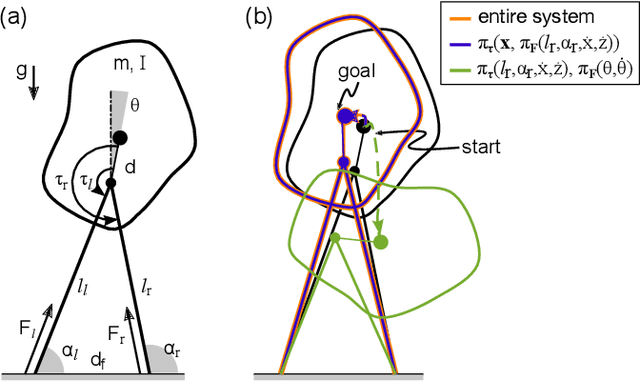
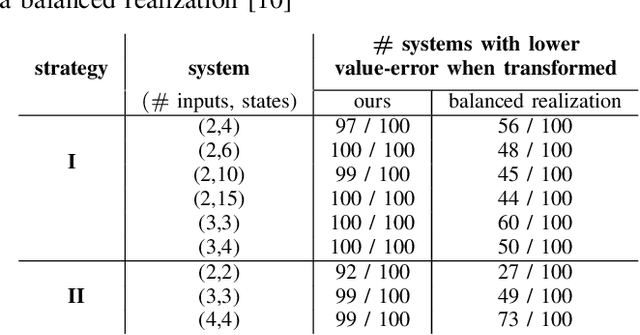
Numerically computing global policies to optimal control problems for complex dynamical systems is mostly intractable. In consequence, a number of approximation methods have been developed. However, none of the current methods can quantify by how much the resulting control underperforms the elusive globally optimal solution. Here we propose policy decomposition, an approximation method with explicit suboptimality estimates. Our method decomposes the optimal control problem into lower-dimensional subproblems, whose optimal solutions are recombined to build a control policy for the entire system. Many such combinations exist, and we introduce the value error and its LQR and DDP estimates to predict the suboptimality of possible combinations and prioritize the ones that minimize it. Using a cart-pole, a 3-link balancing biped and N-link planar manipulators as example systems, we find that the estimates correctly identify the best combinations, yielding control policies in a fraction of the time it takes to compute the optimal control without a notable sacrifice in closed-loop performance. While more research will be needed to find ways of dealing with the combinatorics of policy decomposition, the results suggest this method could be an effective alternative for approximating optimal control in intractable systems.

Using Deep Reinforcement Learning to Learn High-Level Policies on the ATRIAS Biped

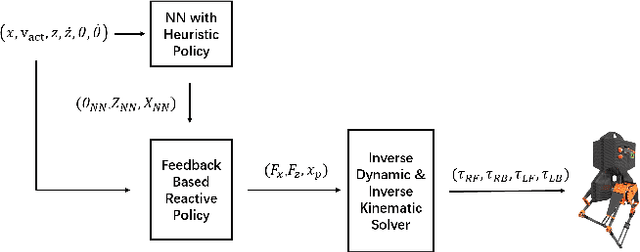
Learning controllers for bipedal robots is a challenging problem, often requiring expert knowledge and extensive tuning of parameters that vary in different situations. Recently, deep reinforcement learning has shown promise at automatically learning controllers for complex systems in simulation. This has been followed by a push towards learning controllers that can be transferred between simulation and hardware, primarily with the use of domain randomization. However, domain randomization can make the problem of finding stable controllers even more challenging, especially for underactuated bipedal robots. In this work, we explore whether policies learned in simulation can be transferred to hardware with the use of high-fidelity simulators and structured controllers. We learn a neural network policy which is a part of a more structured controller. While the neural network is learned in simulation, the rest of the controller stays fixed, and can be tuned by the expert as needed. We show that using this approach can greatly speed up the rate of learning in simulation, as well as enable transfer of policies between simulation and hardware. We present our results on an ATRIAS robot and explore the effect of action spaces and cost functions on the rate of transfer between simulation and hardware. Our results show that structured policies can indeed be learned in simulation and implemented on hardware successfully. This has several advantages, as the structure preserves the intuitive nature of the policy, and the neural network improves the performance of the hand-designed policy. In this way, we propose a way of using neural networks to improve expert designed controllers, while maintaining ease of understanding.

Bayesian Optimization Using Domain Knowledge on the ATRIAS Biped

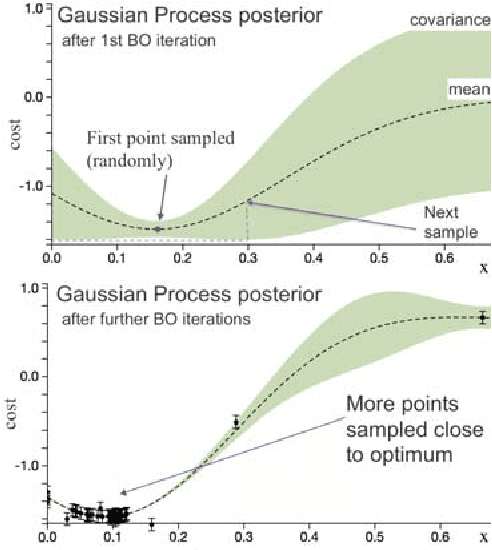
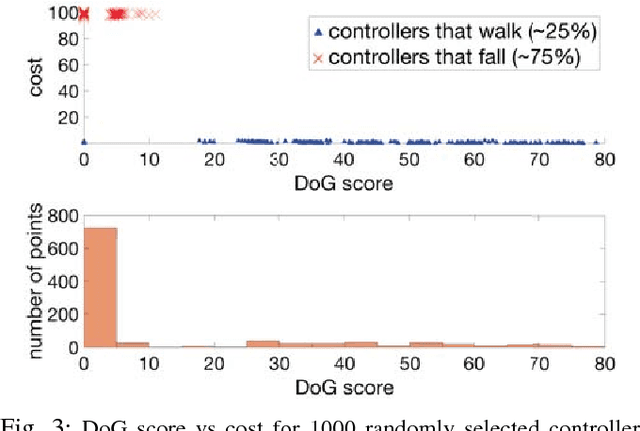
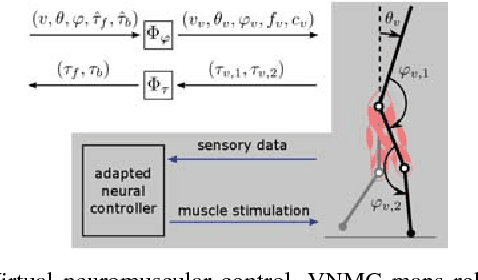
Controllers in robotics often consist of expert-designed heuristics, which can be hard to tune in higher dimensions. It is typical to use simulation to learn these parameters, but controllers learned in simulation often don't transfer to hardware. This necessitates optimization directly on hardware. However, collecting data on hardware can be expensive. This has led to a recent interest in adapting data-efficient learning techniques to robotics. One popular method is Bayesian Optimization (BO), a sample-efficient black-box optimization scheme, but its performance typically degrades in higher dimensions. We aim to overcome this problem by incorporating domain knowledge to reduce dimensionality in a meaningful way, with a focus on bipedal locomotion. In previous work, we proposed a transformation based on knowledge of human walking that projected a 16-dimensional controller to a 1-dimensional space. In simulation, this showed enhanced sample efficiency when optimizing human-inspired neuromuscular walking controllers on a humanoid model. In this paper, we present a generalized feature transform applicable to non-humanoid robot morphologies and evaluate it on the ATRIAS bipedal robot -- in simulation and on hardware. We present three different walking controllers; two are evaluated on the real robot. Our results show that this feature transform captures important aspects of walking and accelerates learning on hardware and simulation, as compared to traditional BO.