Sparsity Inducing Representations for Policy Decompositions

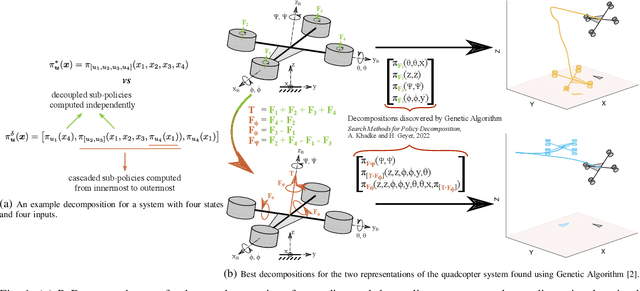
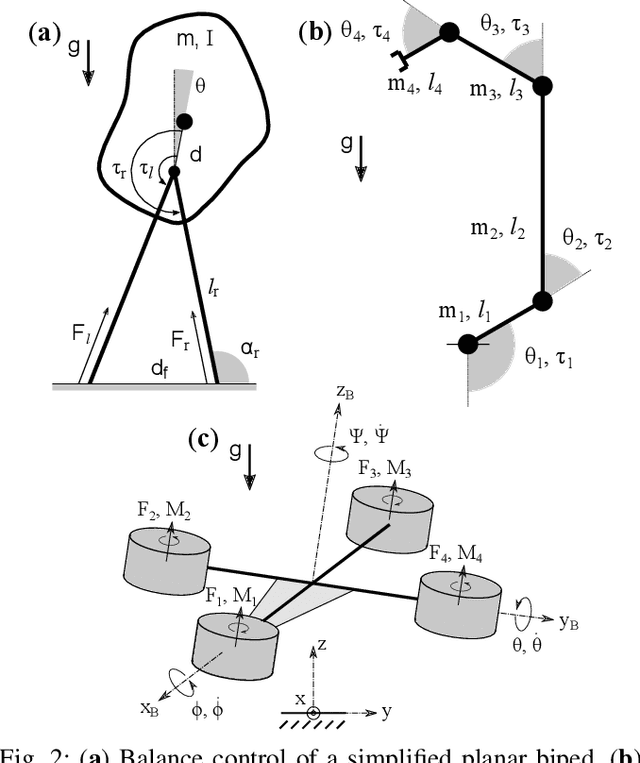
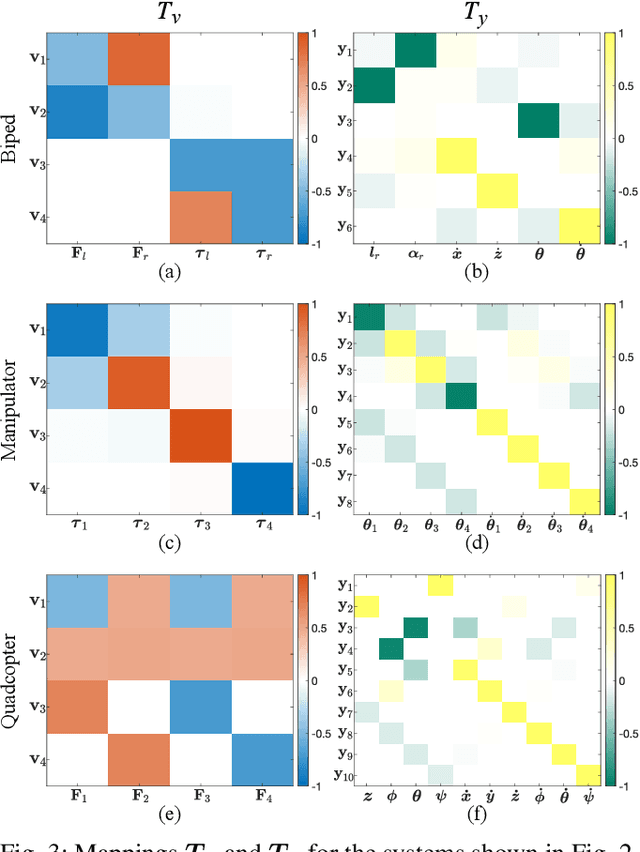
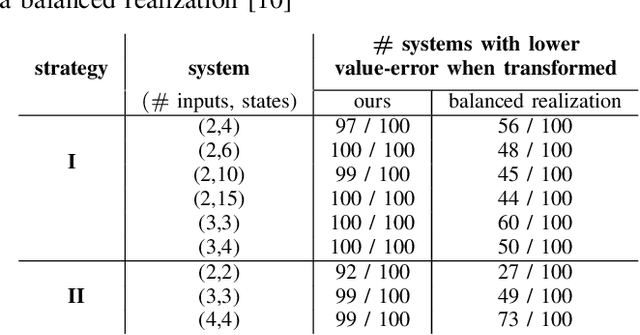
Policy Decomposition (PoDec) is a framework that lessens the curse of dimensionality when deriving policies to optimal control problems. For a given system representation, i.e. the state variables and control inputs describing a system, PoDec generates strategies to decompose the joint optimization of policies for all control inputs. Thereby, policies for different inputs are derived in a decoupled or cascaded fashion and as functions of some subsets of the state variables, leading to reduction in computation. However, the choice of system representation is crucial as it dictates the suboptimality of the resulting policies. We present a heuristic method to find a representation more amenable to decomposition. Our approach is based on the observation that every decomposition enforces a sparsity pattern in the resulting policies at the cost of optimality and a representation that already leads to a sparse optimal policy is likely to produce decompositions with lower suboptimalities. As the optimal policy is not known we construct a system representation that sparsifies its LQR approximation. For a simplified biped, a 4 degree-of-freedom manipulator, and a quadcopter, we discover decompositions that offer 10% reduction in trajectory costs over those identified by vanilla PoDec. Moreover, the decomposition policies produce trajectories with substantially lower costs compared to policies obtained from state-of-the-art reinforcement learning algorithms.

Search Methods for Policy Decompositions

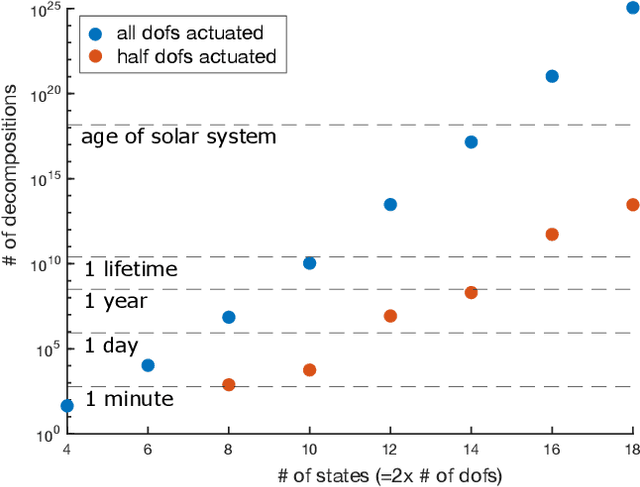
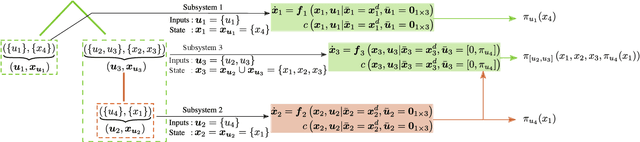
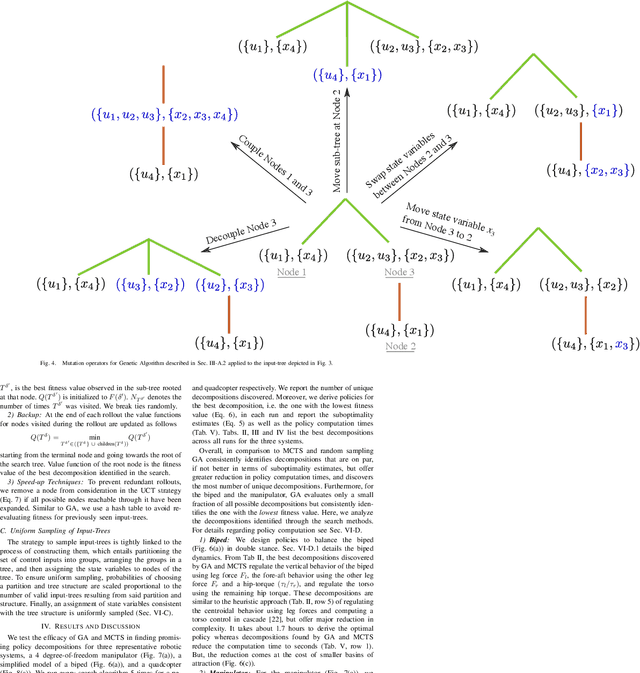
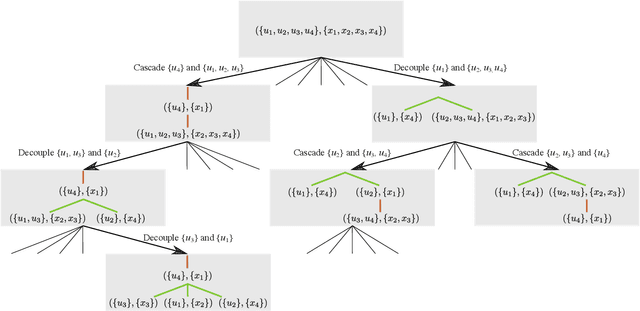
Computing optimal control policies for complex dynamical systems requires approximation methods to remain computationally tractable. Several approximation methods have been developed to tackle this problem. However, these methods do not reason about the suboptimality induced in the resulting control policies due to these approximations. We introduced Policy Decomposition, an approximation method that provides a suboptimality estimate, in our earlier work. Policy decomposition proposes strategies to break an optimal control problem into lower-dimensional subproblems, whose optimal solutions are combined to build a control policy for the original system. However, the number of possible strategies to decompose a system scale quickly with the complexity of a system, posing a combinatorial challenge. In this work we investigate the use of Genetic Algorithm and Monte-Carlo Tree Search to alleviate this challenge. We identify decompositions for swing-up control of a 4 degree-of-freedom manipulator, balance control of a simplified biped, and hover control of a quadcopter.

Policy Decomposition: Approximate Optimal Control with Suboptimality Estimates

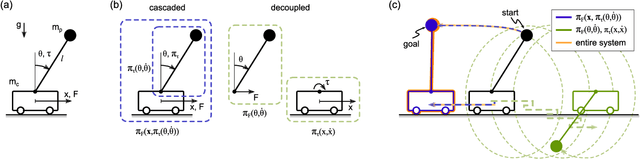
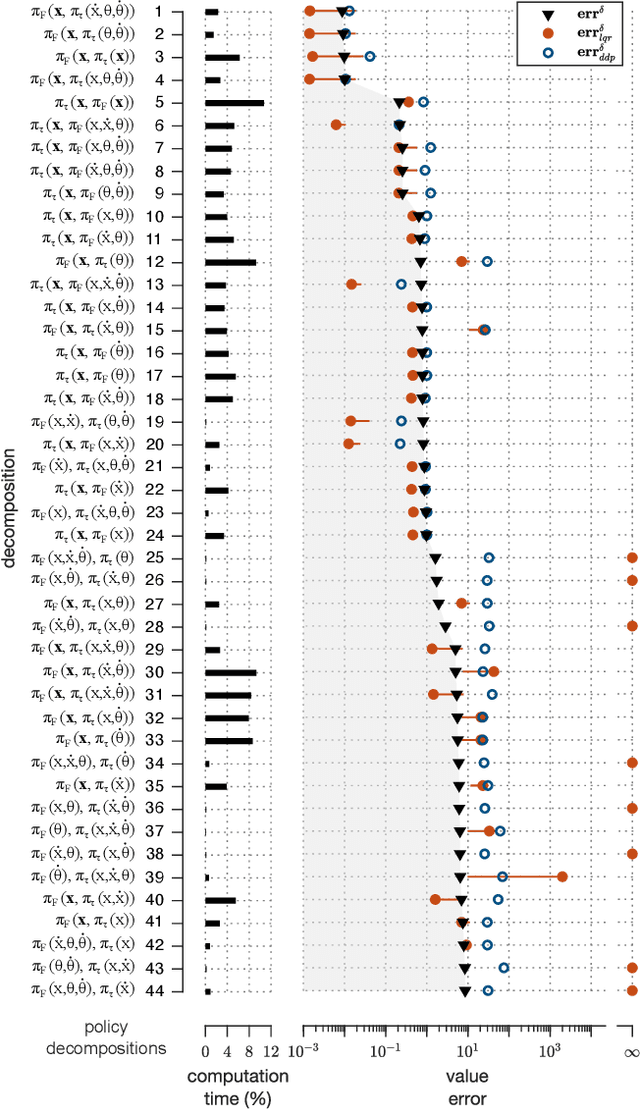
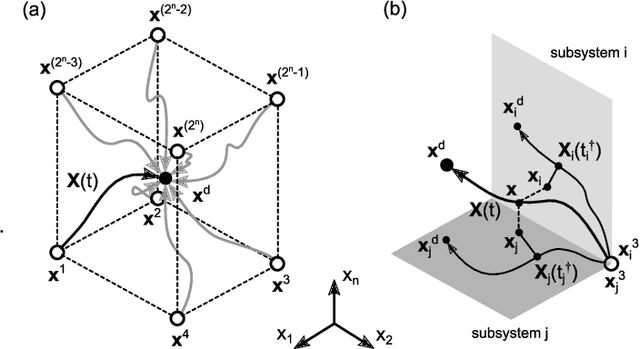
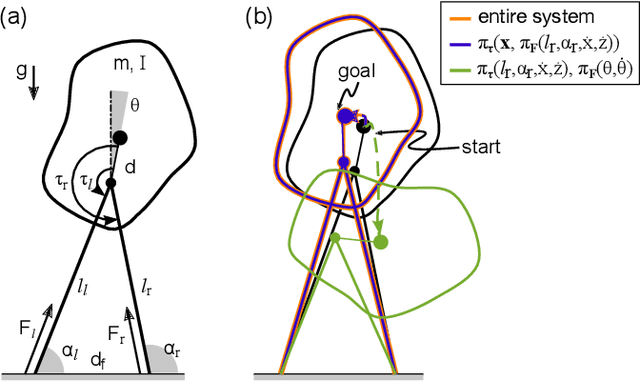
Numerically computing global policies to optimal control problems for complex dynamical systems is mostly intractable. In consequence, a number of approximation methods have been developed. However, none of the current methods can quantify by how much the resulting control underperforms the elusive globally optimal solution. Here we propose policy decomposition, an approximation method with explicit suboptimality estimates. Our method decomposes the optimal control problem into lower-dimensional subproblems, whose optimal solutions are recombined to build a control policy for the entire system. Many such combinations exist, and we introduce the value error and its LQR and DDP estimates to predict the suboptimality of possible combinations and prioritize the ones that minimize it. Using a cart-pole, a 3-link balancing biped and N-link planar manipulators as example systems, we find that the estimates correctly identify the best combinations, yielding control policies in a fraction of the time it takes to compute the optimal control without a notable sacrifice in closed-loop performance. While more research will be needed to find ways of dealing with the combinatorics of policy decomposition, the results suggest this method could be an effective alternative for approximating optimal control in intractable systems.

What Can This Robot Do? Learning from Appearance and Experiments

When presented with an unknown robot (subject) how can an autonomous agent (learner) figure out what this new robot can do? The subject's appearance can provide cues to its physical as well as cognitive capabilities. Seeing a humanoid can make one wonder if it can kick balls, climb stairs or recognize faces. What if the learner can request the subject to perform these tasks? We present an approach to make the learner build a model of the subject at a task based on the latter's appearance and refine it by experimentation. Apart from the subject's inherent capabilities, certain extrinsic factors may affect its performance at a task. Based on the subject's appearance and prior knowledge about the task a learner can identify a set of potential factors, a subset of which we assume are controllable. Our approach picks values of controllable factors to generate the most informative experiments to test the subject at. Additionally, we present a metric to determine if a factor should be incorporated in the model. We present results of our approach on modeling a humanoid robot at the task of kicking a ball. Firstly, we show that actively picking values for controllable factors, even in noisy experiments, leads to faster learning of the subject's model for the task. Secondly, starting from a minimal set of factors our metric identifies the set of relevant factors to incorporate in the model. Lastly, we show that the refined model better represents the subject's performance at the task.