Sparsity Inducing Representations for Policy Decompositions
Paper and Code
Sep 15, 2022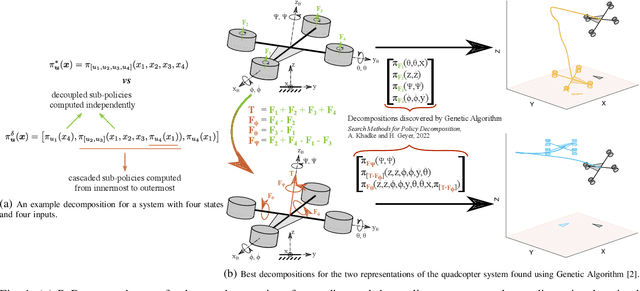
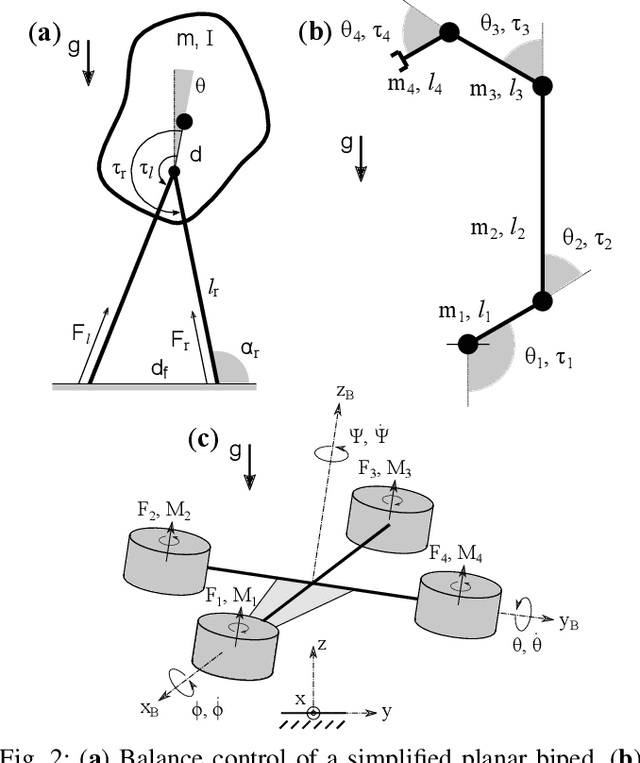
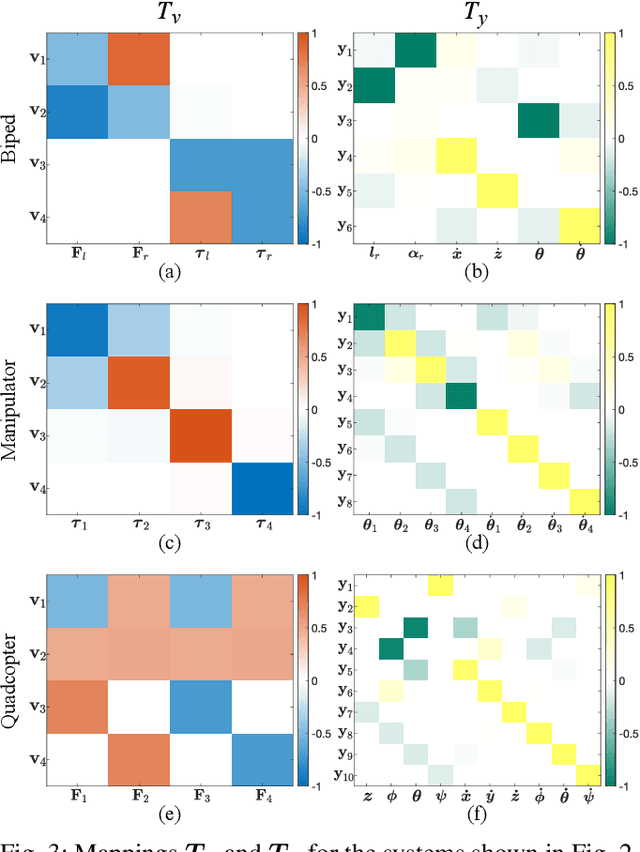
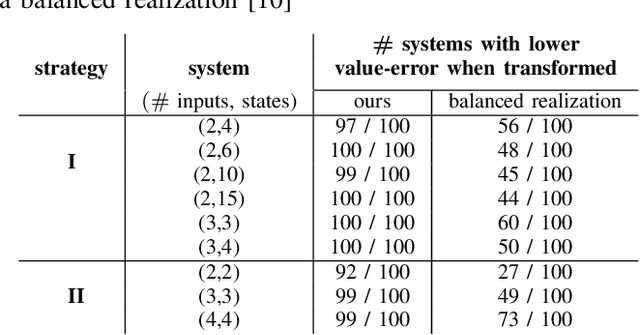
Policy Decomposition (PoDec) is a framework that lessens the curse of dimensionality when deriving policies to optimal control problems. For a given system representation, i.e. the state variables and control inputs describing a system, PoDec generates strategies to decompose the joint optimization of policies for all control inputs. Thereby, policies for different inputs are derived in a decoupled or cascaded fashion and as functions of some subsets of the state variables, leading to reduction in computation. However, the choice of system representation is crucial as it dictates the suboptimality of the resulting policies. We present a heuristic method to find a representation more amenable to decomposition. Our approach is based on the observation that every decomposition enforces a sparsity pattern in the resulting policies at the cost of optimality and a representation that already leads to a sparse optimal policy is likely to produce decompositions with lower suboptimalities. As the optimal policy is not known we construct a system representation that sparsifies its LQR approximation. For a simplified biped, a 4 degree-of-freedom manipulator, and a quadcopter, we discover decompositions that offer 10% reduction in trajectory costs over those identified by vanilla PoDec. Moreover, the decomposition policies produce trajectories with substantially lower costs compared to policies obtained from state-of-the-art reinforcement learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge