Policy Decomposition: Approximate Optimal Control with Suboptimality Estimates
Paper and Code
Mar 03, 2021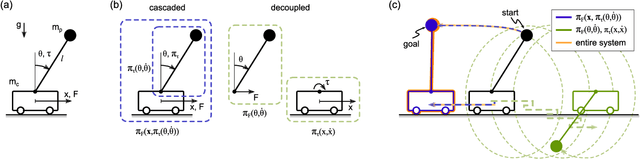
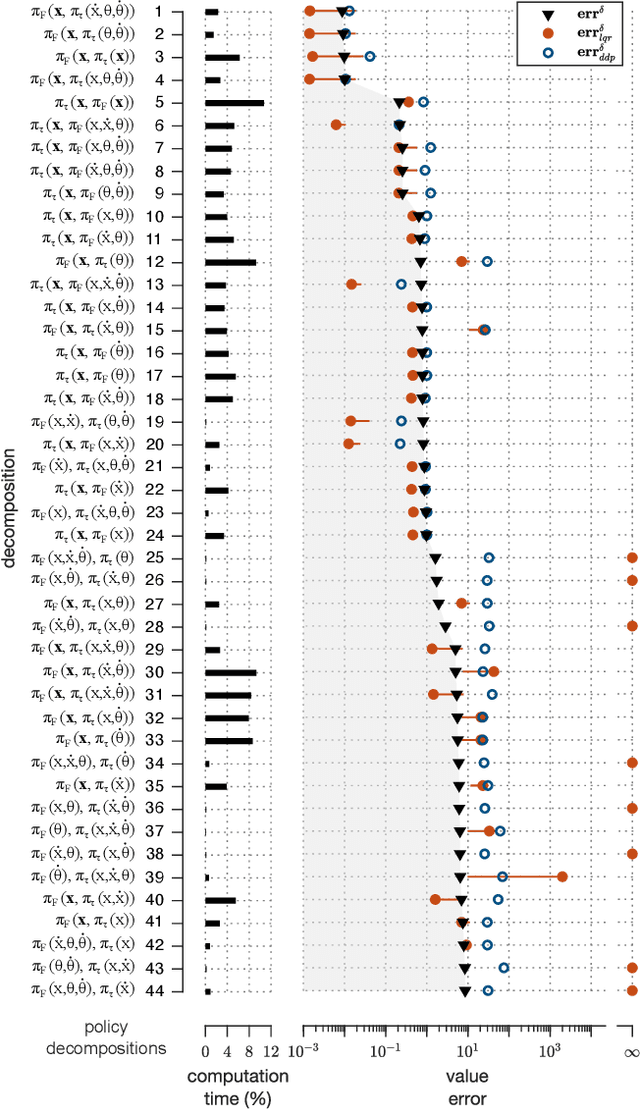
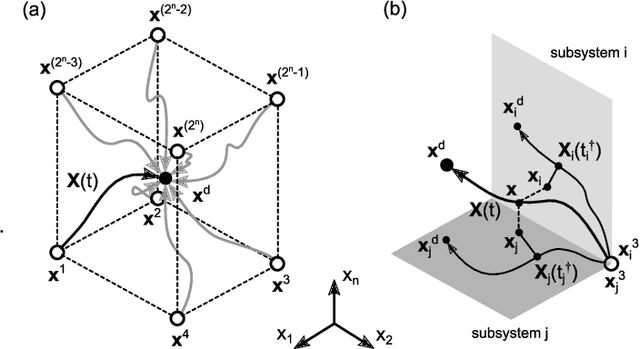
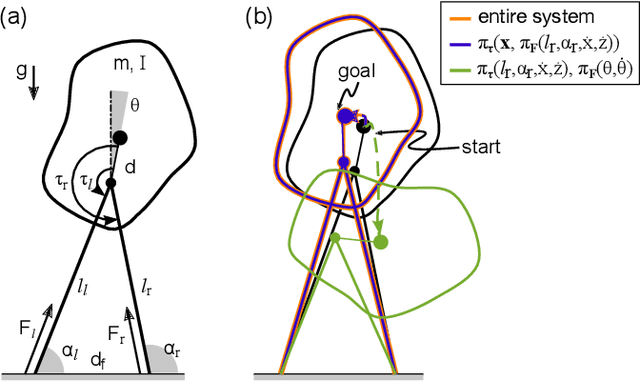
Numerically computing global policies to optimal control problems for complex dynamical systems is mostly intractable. In consequence, a number of approximation methods have been developed. However, none of the current methods can quantify by how much the resulting control underperforms the elusive globally optimal solution. Here we propose policy decomposition, an approximation method with explicit suboptimality estimates. Our method decomposes the optimal control problem into lower-dimensional subproblems, whose optimal solutions are recombined to build a control policy for the entire system. Many such combinations exist, and we introduce the value error and its LQR and DDP estimates to predict the suboptimality of possible combinations and prioritize the ones that minimize it. Using a cart-pole, a 3-link balancing biped and N-link planar manipulators as example systems, we find that the estimates correctly identify the best combinations, yielding control policies in a fraction of the time it takes to compute the optimal control without a notable sacrifice in closed-loop performance. While more research will be needed to find ways of dealing with the combinatorics of policy decomposition, the results suggest this method could be an effective alternative for approximating optimal control in intractable systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge