Search Methods for Policy Decompositions
Paper and Code
Mar 29, 2022
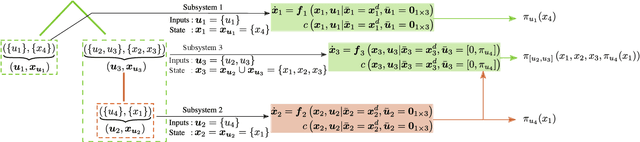
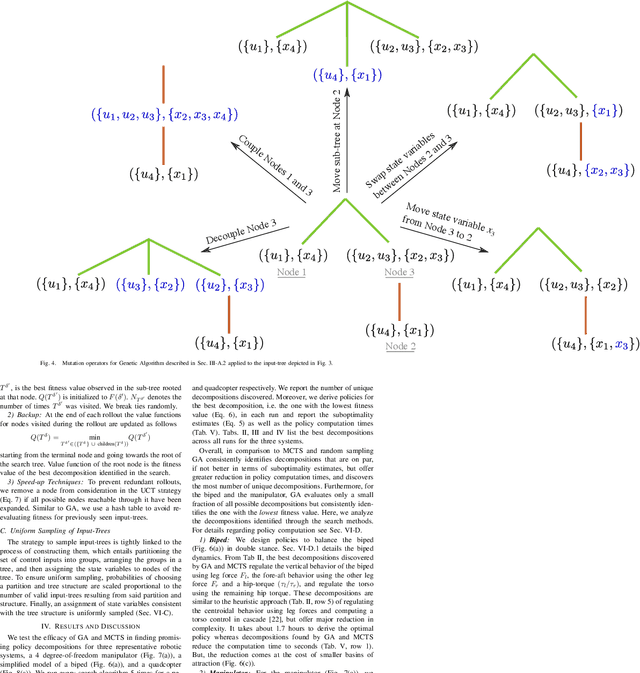
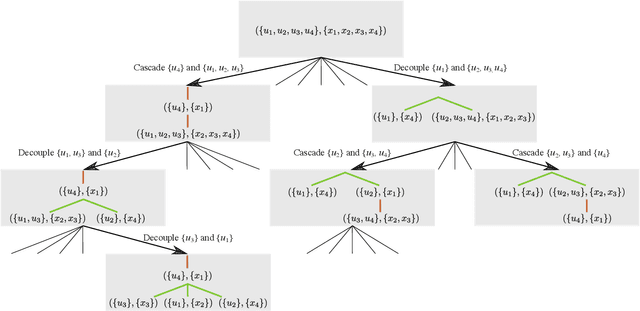
Computing optimal control policies for complex dynamical systems requires approximation methods to remain computationally tractable. Several approximation methods have been developed to tackle this problem. However, these methods do not reason about the suboptimality induced in the resulting control policies due to these approximations. We introduced Policy Decomposition, an approximation method that provides a suboptimality estimate, in our earlier work. Policy decomposition proposes strategies to break an optimal control problem into lower-dimensional subproblems, whose optimal solutions are combined to build a control policy for the original system. However, the number of possible strategies to decompose a system scale quickly with the complexity of a system, posing a combinatorial challenge. In this work we investigate the use of Genetic Algorithm and Monte-Carlo Tree Search to alleviate this challenge. We identify decompositions for swing-up control of a 4 degree-of-freedom manipulator, balance control of a simplified biped, and hover control of a quadcopter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge