Fetpype: An Open-Source Pipeline for Reproducible Fetal Brain MRI Analysis

Fetal brain Magnetic Resonance Imaging (MRI) is crucial for assessing neurodevelopment in utero. However, analyzing this data presents significant challenges due to fetal motion, low signal-to-noise ratio, and the need for complex multi-step processing, including motion correction, super-resolution reconstruction, segmentation, and surface extraction. While various specialized tools exist for individual steps, integrating them into robust, reproducible, and user-friendly workflows that go from raw images to processed volumes is not straightforward. This lack of standardization hinders reproducibility across studies and limits the adoption of advanced analysis techniques for researchers and clinicians. To address these challenges, we introduce Fetpype, an open-source Python library designed to streamline and standardize the preprocessing and analysis of T2-weighted fetal brain MRI data. Fetpype is publicly available on GitHub at https://github.com/fetpype/fetpype.

Fast and Explicit: Slice-to-Volume Reconstruction via 3D Gaussian Primitives with Analytic Point Spread Function Modeling

Recovering high-fidelity 3D images from sparse or degraded 2D images is a fundamental challenge in medical imaging, with broad applications ranging from 3D ultrasound reconstruction to MRI super-resolution. In the context of fetal MRI, high-resolution 3D reconstruction of the brain from motion-corrupted low-resolution 2D acquisitions is a prerequisite for accurate neurodevelopmental diagnosis. While implicit neural representations (INRs) have recently established state-of-the-art performance in self-supervised slice-to-volume reconstruction (SVR), they suffer from a critical computational bottleneck: accurately modeling the image acquisition physics requires expensive stochastic Monte Carlo sampling to approximate the point spread function (PSF). In this work, we propose a shift from neural network based implicit representations to Gaussian based explicit representations. By parameterizing the HR 3D image volume as a field of anisotropic Gaussian primitives, we leverage the property of Gaussians being closed under convolution and thus derive a \textit{closed-form analytical solution} for the forward model. This formulation reduces the previously intractable acquisition integral to an exact covariance addition ($\mathbfΣ_{obs} = \mathbfΣ_{HR} + \mathbfΣ_{PSF}$), effectively bypassing the need for compute-intensive stochastic sampling while ensuring exact gradient propagation. We demonstrate that our approach matches the reconstruction quality of self-supervised state-of-the-art SVR frameworks while delivering a 5$\times$--10$\times$ speed-up on neonatal and fetal data. With convergence often reached in under 30 seconds, our framework paves the way towards translation into clinical routine of real-time fetal 3D MRI. Code will be public at {https://github.com/m-dannecker/Gaussian-Primitives-for-Fast-SVR}.

CINeMA: Conditional Implicit Neural Multi-Modal Atlas for a Spatio-Temporal Representation of the Perinatal Brain

Magnetic resonance imaging of fetal and neonatal brains reveals rapid neurodevelopment marked by substantial anatomical changes unfolding within days. Studying this critical stage of the developing human brain, therefore, requires accurate brain models-referred to as atlases-of high spatial and temporal resolution. To meet these demands, established traditional atlases and recently proposed deep learning-based methods rely on large and comprehensive datasets. This poses a major challenge for studying brains in the presence of pathologies for which data remains scarce. We address this limitation with CINeMA (Conditional Implicit Neural Multi-Modal Atlas), a novel framework for creating high-resolution, spatio-temporal, multimodal brain atlases, suitable for low-data settings. Unlike established methods, CINeMA operates in latent space, avoiding compute-intensive image registration and reducing atlas construction times from days to minutes. Furthermore, it enables flexible conditioning on anatomical features including GA, birth age, and pathologies like ventriculomegaly (VM) and agenesis of the corpus callosum (ACC). CINeMA supports downstream tasks such as tissue segmentation and age prediction whereas its generative properties enable synthetic data creation and anatomically informed data augmentation. Surpassing state-of-the-art methods in accuracy, efficiency, and versatility, CINeMA represents a powerful tool for advancing brain research. We release the code and atlases at https://github.com/m-dannecker/CINeMA.

Automatic quality control in multi-centric fetal brain MRI super-resolution reconstruction

Quality control (QC) has long been considered essential to guarantee the reliability of neuroimaging studies. It is particularly important for fetal brain MRI, where acquisitions and image processing techniques are less standardized than in adult imaging. In this work, we focus on automated quality control of super-resolution reconstruction (SRR) volumes of fetal brain MRI, an important processing step where multiple stacks of thick 2D slices are registered together and combined to build a single, isotropic and artifact-free T2 weighted volume. We propose FetMRQC$_{SR}$, a machine-learning method that extracts more than 100 image quality metrics to predict image quality scores using a random forest model. This approach is well suited to a problem that is high dimensional, with highly heterogeneous data and small datasets. We validate FetMRQC$_{SR}$ in an out-of-domain (OOD) setting and report high performance (ROC AUC = 0.89), even when faced with data from an unknown site or SRR method. We also investigate failure cases and show that they occur in $45\%$ of the images due to ambiguous configurations for which the rating from the expert is arguable. These results are encouraging and illustrate how a non deep learning-based method like FetMRQC$_{SR}$ is well suited to this multifaceted problem. Our tool, along with all the code used to generate, train and evaluate the model will be released upon acceptance of the paper.

$DPF^*$: improved Depth Potential Function for scale-invariant sulcal depth estimation

The shape of human brain is complex and highly variable, with interactions between brain size, cortical folding, and age well-documented in the literature. However, few studies have explored how global brain size influences geometric features of the cortical surface derived from anatomical MRI. In this work, we focus on sulcal depth, an imaging phenotype that has gained significant attention in both basic research and clinical applications. We make key contributions to the field by: 1) providing the first quantitative analysis of how brain size affects sulcal depth measurements; 2) introducing a novel, scale-invariant method for sulcal depth estimation based on an original formalization of the problem; 3) presenting a validation framework and sharing our code and benchmark data with the community; and 4) demonstrating the biological relevance of our new sulcal depth measure using a large sample of 1,987 subjects spanning the developmental period from 26 weeks post-conception to adulthood.

FetMRQC: an open-source machine learning framework for multi-centric fetal brain MRI quality control

Fetal brain MRI is becoming an increasingly relevant complement to neurosonography for perinatal diagnosis, allowing fundamental insights into fetal brain development throughout gestation. However, uncontrolled fetal motion and heterogeneity in acquisition protocols lead to data of variable quality, potentially biasing the outcome of subsequent studies. We present FetMRQC, an open-source machine-learning framework for automated image quality assessment and quality control that is robust to domain shifts induced by the heterogeneity of clinical data. FetMRQC extracts an ensemble of quality metrics from unprocessed anatomical MRI and combines them to predict experts' ratings using random forests. We validate our framework on a pioneeringly large and diverse dataset of more than 1600 manually rated fetal brain T2-weighted images from four clinical centers and 13 different scanners. Our study shows that FetMRQC's predictions generalize well to unseen data while being interpretable. FetMRQC is a step towards more robust fetal brain neuroimaging, which has the potential to shed new insights on the developing human brain.

Population-wise Labeling of Sulcal Graphs using Multi-graph Matching

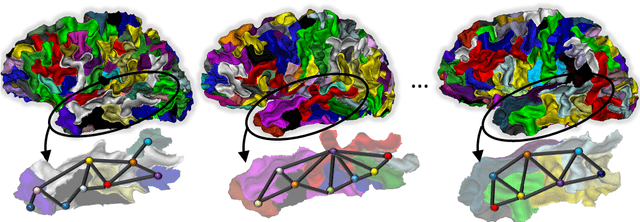
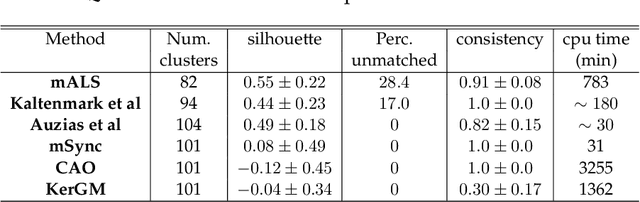
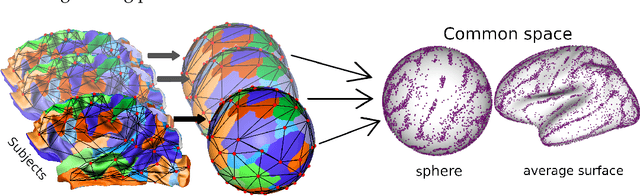
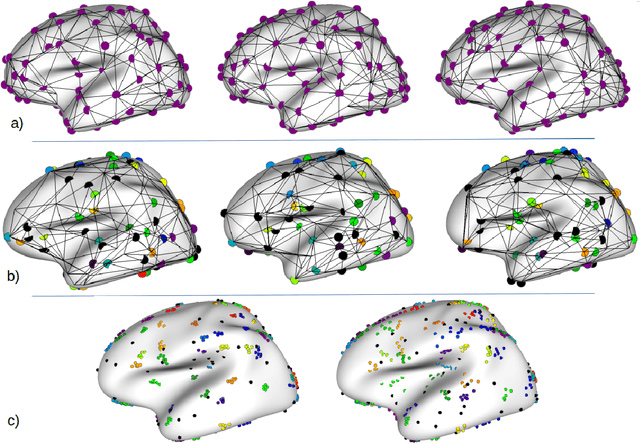
Population-wise matching of the cortical fold is necessary to identify biomarkers of neurological or psychiatric disorders. The difficulty comes from the massive interindividual variations in the morphology and spatial organization of the folds. This task is challenging at both methodological and conceptual levels. In the widely used registration-based techniques, these variations are considered as noise and the matching of folds is only implicit. Alternative approaches are based on the extraction and explicit identification of the cortical folds. In particular, representing cortical folding patterns as graphs of sulcal basins-termed sulcal graphs-enables to formalize the task as a graph-matching problem. In this paper, we propose to address the problem of sulcal graph matching directly at the population level using multi-graph matching techniques. First, we motivate the relevance of multi-graph matching framework in this context. We then introduce a procedure to generate populations of artificial sulcal graphs, which allows us benchmarking several state of the art multi-graph matching methods. Our results on both artificial and real data demonstrate the effectiveness of multi-graph matching techniques to obtain a population-wise consistent labeling of cortical folds at the sulcal basins level.

Kernelized multi-graph matching

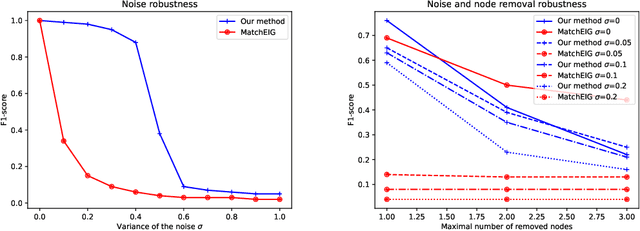
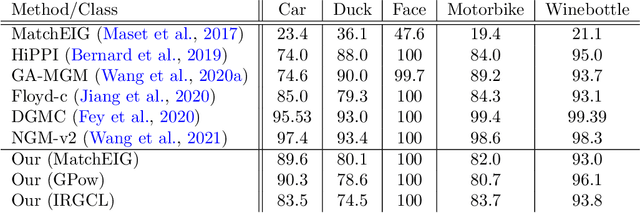
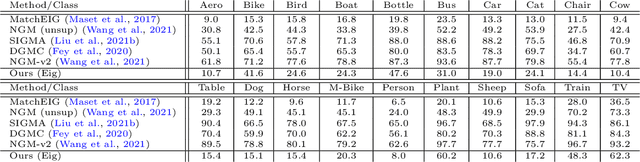
Multigraph matching is a recent variant of the graph matching problem. In this framework, the optimization procedure considers several graphs and enforces the consistency of the matches along the graphs. This constraint can be formalized as a cycle consistency across the pairwise permutation matrices, which implies the definition of a universe of vertex~\citep{pachauri2013solving}. The label of each vertex is encoded by a sparse vector and the dimension of this space corresponds to the rank of the bulk permutation matrix, the matrix built from the aggregation of all the pairwise permutation matrices. The matching problem can then be formulated as a non-convex quadratic optimization problem (QAP) under constraints imposed on the rank and the permutations. In this paper, we introduce a novel kernelized multigraph matching technique that handles vectors of attributes on both the vertices and edges of the graphs, while maintaining a low memory usage. We solve the QAP problem using a projected power optimization approach and propose several projectors leading to improved stability of the results. We provide several experiments showing that our method is competitive against other unsupervised methods.

Comparing vector fields across surfaces: interest for characterizing the orientations of cortical folds

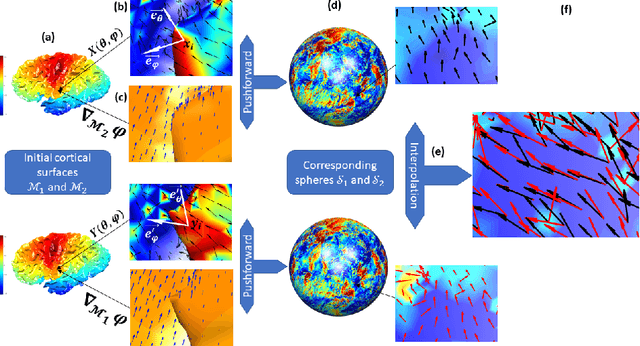
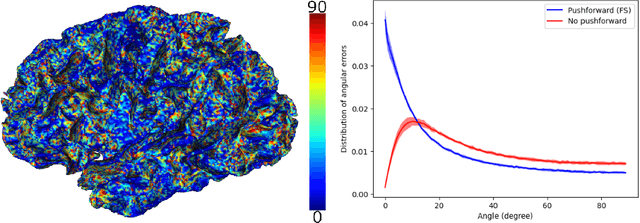
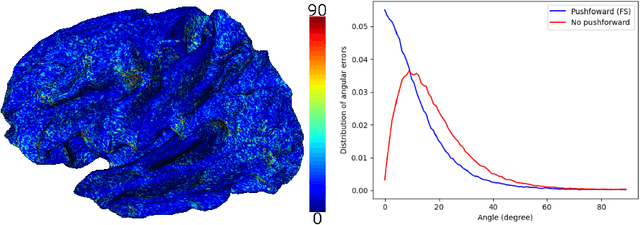
Vectors fields defined on surfaces constitute relevant and useful representations but are rarely used. One reason might be that comparing vector fields across two surfaces of the same genus is not trivial: it requires to transport the vector fields from the original surfaces onto a common domain. In this paper, we propose a framework to achieve this task by mapping the vector fields onto a common space, using some notions of differential geometry. The proposed framework enables the computation of statistics on vector fields. We demonstrate its interest in practice with an application on real data with a quantitative assessment of the reproducibility of curvature directions that describe the complex geometry of cortical folding patterns. The proposed framework is general and can be applied to different types of vector fields and surfaces, allowing for a large number of high potential applications in medical imaging.