$DPF^*$: improved Depth Potential Function for scale-invariant sulcal depth estimation

The shape of human brain is complex and highly variable, with interactions between brain size, cortical folding, and age well-documented in the literature. However, few studies have explored how global brain size influences geometric features of the cortical surface derived from anatomical MRI. In this work, we focus on sulcal depth, an imaging phenotype that has gained significant attention in both basic research and clinical applications. We make key contributions to the field by: 1) providing the first quantitative analysis of how brain size affects sulcal depth measurements; 2) introducing a novel, scale-invariant method for sulcal depth estimation based on an original formalization of the problem; 3) presenting a validation framework and sharing our code and benchmark data with the community; and 4) demonstrating the biological relevance of our new sulcal depth measure using a large sample of 1,987 subjects spanning the developmental period from 26 weeks post-conception to adulthood.

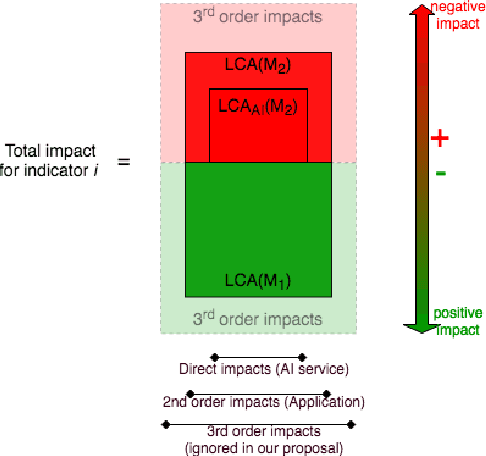
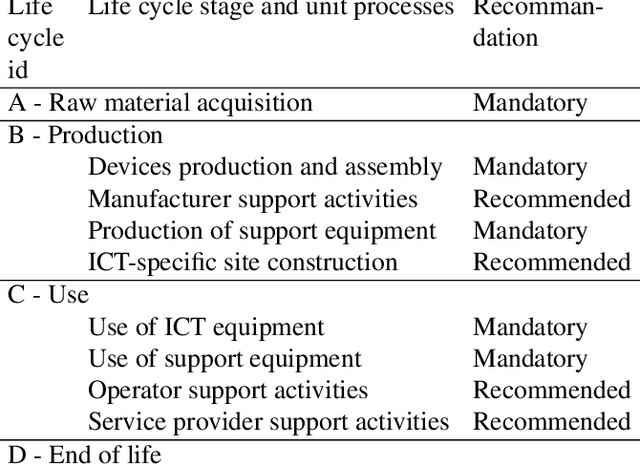
Unraveling the hidden environmental impacts of AI solutions for environment

In the past ten years artificial intelligence has encountered such dramatic progress that it is seen now as a tool of choice to solve environmental issues and in the first place greenhouse gas emissions (GHG). At the same time the deep learning community began to realize that training models with more and more parameters required a lot of energy and as a consequence GHG emissions. To our knowledge, questioning the complete environmental impacts of AI methods for environment ("AI for green"), and not only GHG, has never been addressed directly. In this article we propose to study the possible negative impact of "AI for green" 1) by reviewing first the different types of AI impacts 2) by presenting the different methodologies used to assess those impacts, in particular life cycle assessment and 3) by discussing how to assess the environmental usefulness of a general AI service.

Comparing vector fields across surfaces: interest for characterizing the orientations of cortical folds

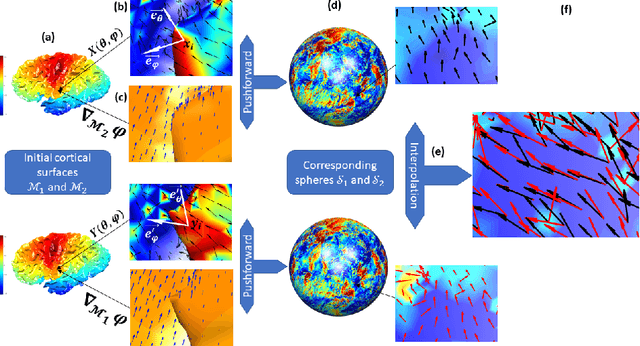
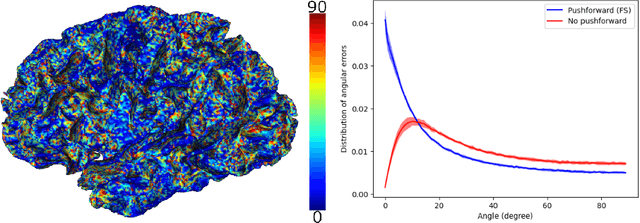
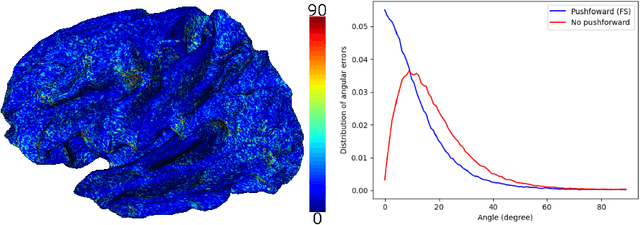
Vectors fields defined on surfaces constitute relevant and useful representations but are rarely used. One reason might be that comparing vector fields across two surfaces of the same genus is not trivial: it requires to transport the vector fields from the original surfaces onto a common domain. In this paper, we propose a framework to achieve this task by mapping the vector fields onto a common space, using some notions of differential geometry. The proposed framework enables the computation of statistics on vector fields. We demonstrate its interest in practice with an application on real data with a quantitative assessment of the reproducibility of curvature directions that describe the complex geometry of cortical folding patterns. The proposed framework is general and can be applied to different types of vector fields and surfaces, allowing for a large number of high potential applications in medical imaging.