Comparing vector fields across surfaces: interest for characterizing the orientations of cortical folds
Paper and Code
Jun 14, 2021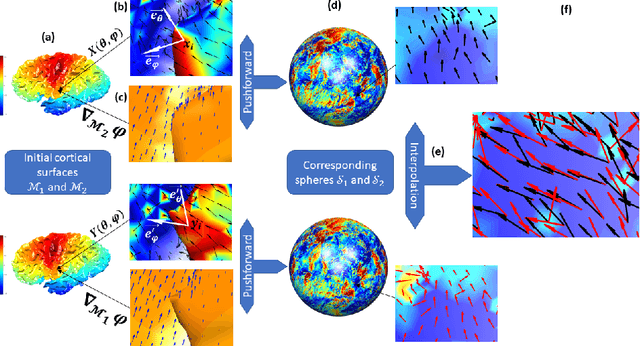
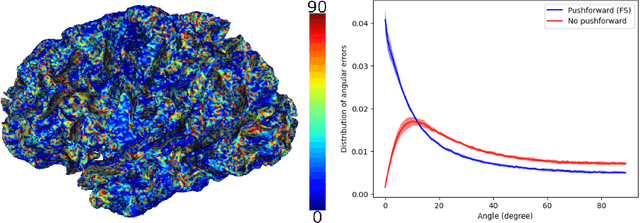
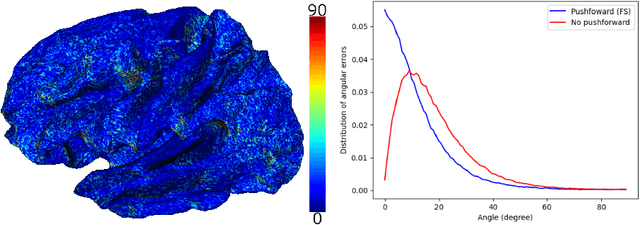
Vectors fields defined on surfaces constitute relevant and useful representations but are rarely used. One reason might be that comparing vector fields across two surfaces of the same genus is not trivial: it requires to transport the vector fields from the original surfaces onto a common domain. In this paper, we propose a framework to achieve this task by mapping the vector fields onto a common space, using some notions of differential geometry. The proposed framework enables the computation of statistics on vector fields. We demonstrate its interest in practice with an application on real data with a quantitative assessment of the reproducibility of curvature directions that describe the complex geometry of cortical folding patterns. The proposed framework is general and can be applied to different types of vector fields and surfaces, allowing for a large number of high potential applications in medical imaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge