Population-wise Labeling of Sulcal Graphs using Multi-graph Matching

Population-wise matching of the cortical fold is necessary to identify biomarkers of neurological or psychiatric disorders. The difficulty comes from the massive interindividual variations in the morphology and spatial organization of the folds. This task is challenging at both methodological and conceptual levels. In the widely used registration-based techniques, these variations are considered as noise and the matching of folds is only implicit. Alternative approaches are based on the extraction and explicit identification of the cortical folds. In particular, representing cortical folding patterns as graphs of sulcal basins-termed sulcal graphs-enables to formalize the task as a graph-matching problem. In this paper, we propose to address the problem of sulcal graph matching directly at the population level using multi-graph matching techniques. First, we motivate the relevance of multi-graph matching framework in this context. We then introduce a procedure to generate populations of artificial sulcal graphs, which allows us benchmarking several state of the art multi-graph matching methods. Our results on both artificial and real data demonstrate the effectiveness of multi-graph matching techniques to obtain a population-wise consistent labeling of cortical folds at the sulcal basins level.

Kernelized multi-graph matching

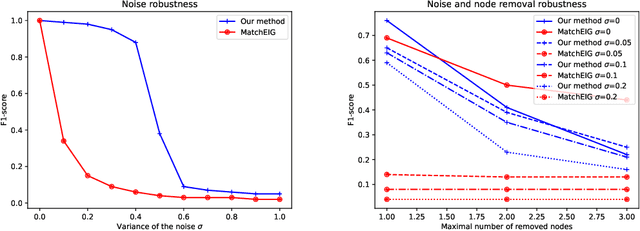
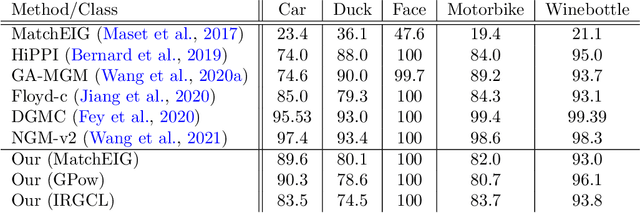
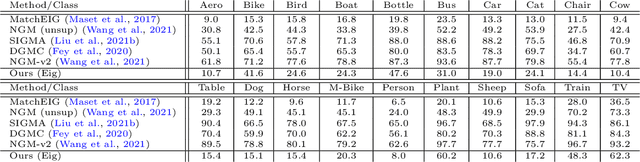
Multigraph matching is a recent variant of the graph matching problem. In this framework, the optimization procedure considers several graphs and enforces the consistency of the matches along the graphs. This constraint can be formalized as a cycle consistency across the pairwise permutation matrices, which implies the definition of a universe of vertex~\citep{pachauri2013solving}. The label of each vertex is encoded by a sparse vector and the dimension of this space corresponds to the rank of the bulk permutation matrix, the matrix built from the aggregation of all the pairwise permutation matrices. The matching problem can then be formulated as a non-convex quadratic optimization problem (QAP) under constraints imposed on the rank and the permutations. In this paper, we introduce a novel kernelized multigraph matching technique that handles vectors of attributes on both the vertices and edges of the graphs, while maintaining a low memory usage. We solve the QAP problem using a projected power optimization approach and propose several projectors leading to improved stability of the results. We provide several experiments showing that our method is competitive against other unsupervised methods.

Mapping individual differences in cortical architecture using multi-view representation learning

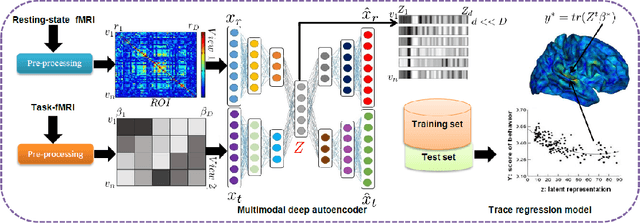
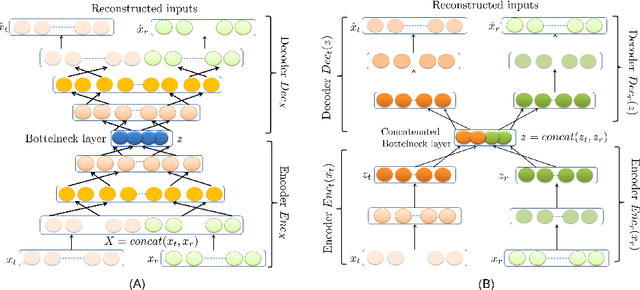
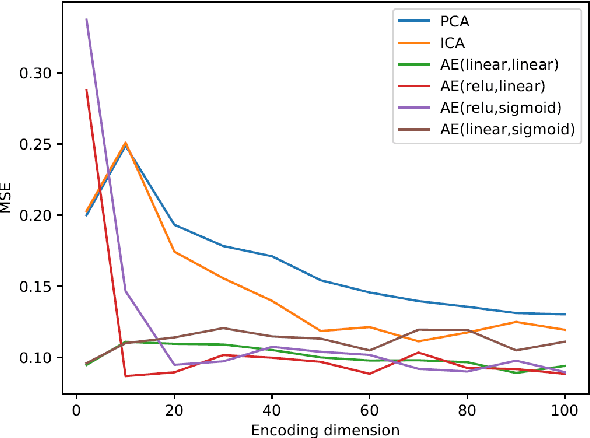
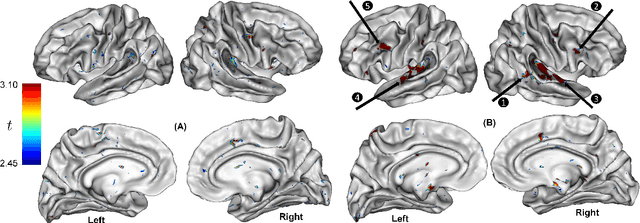
In neuroscience, understanding inter-individual differences has recently emerged as a major challenge, for which functional magnetic resonance imaging (fMRI) has proven invaluable. For this, neuroscientists rely on basic methods such as univariate linear correlations between single brain features and a score that quantifies either the severity of a disease or the subject's performance in a cognitive task. However, to this date, task-fMRI and resting-state fMRI have been exploited separately for this question, because of the lack of methods to effectively combine them. In this paper, we introduce a novel machine learning method which allows combining the activation-and connectivity-based information respectively measured through these two fMRI protocols to identify markers of individual differences in the functional organization of the brain. It combines a multi-view deep autoencoder which is designed to fuse the two fMRI modalities into a joint representation space within which a predictive model is trained to guess a scalar score that characterizes the patient. Our experimental results demonstrate the ability of the proposed method to outperform competitive approaches and to produce interpretable and biologically plausible results.

Hierarchical Bag of Paths for Kernel Based Shape Classification

Graph kernels methods are based on an implicit embedding of graphs within a vector space of large dimension. This implicit embedding allows to apply to graphs methods which where until recently solely reserved to numerical data. Within the shape classification framework, graphs are often produced by a skeletonization step which is sensitive to noise. We propose in this paper to integrate the robustness to structural noise by using a kernel based on a bag of path where each path is associated to a hierarchy encoding successive simplifications of the path. Several experiments prove the robustness and the flexibility of our approach compared to alternative shape classification methods.