Rohit Yadav
AMU, INT, LIS
Population-wise Labeling of Sulcal Graphs using Multi-graph Matching
Jan 31, 2023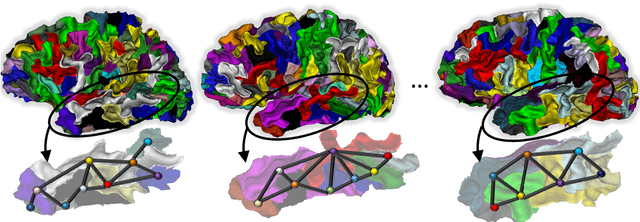
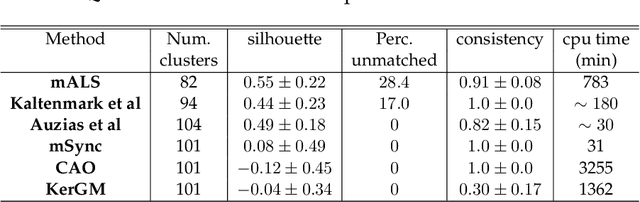
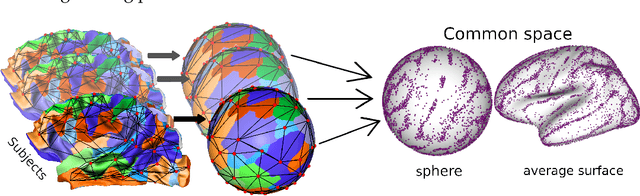
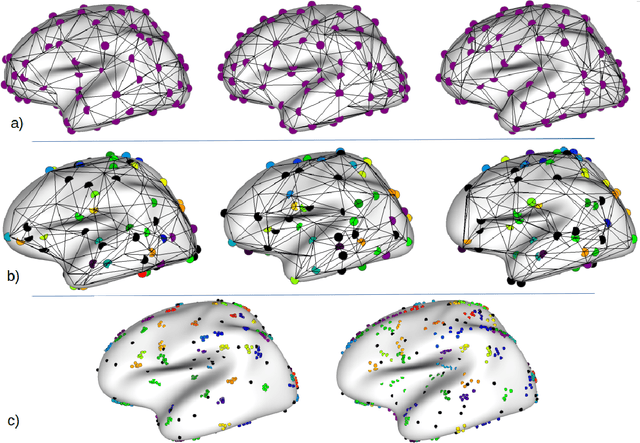
Abstract:Population-wise matching of the cortical fold is necessary to identify biomarkers of neurological or psychiatric disorders. The difficulty comes from the massive interindividual variations in the morphology and spatial organization of the folds. This task is challenging at both methodological and conceptual levels. In the widely used registration-based techniques, these variations are considered as noise and the matching of folds is only implicit. Alternative approaches are based on the extraction and explicit identification of the cortical folds. In particular, representing cortical folding patterns as graphs of sulcal basins-termed sulcal graphs-enables to formalize the task as a graph-matching problem. In this paper, we propose to address the problem of sulcal graph matching directly at the population level using multi-graph matching techniques. First, we motivate the relevance of multi-graph matching framework in this context. We then introduce a procedure to generate populations of artificial sulcal graphs, which allows us benchmarking several state of the art multi-graph matching methods. Our results on both artificial and real data demonstrate the effectiveness of multi-graph matching techniques to obtain a population-wise consistent labeling of cortical folds at the sulcal basins level.
Kernelized multi-graph matching
Oct 11, 2022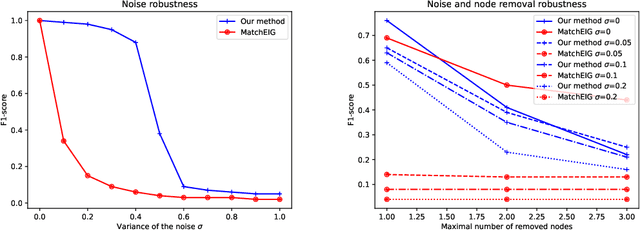
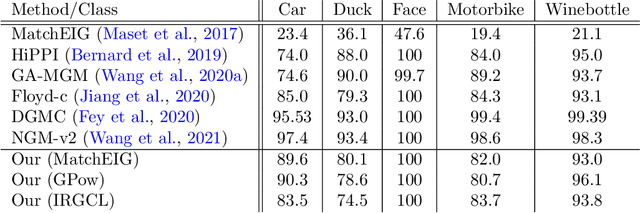
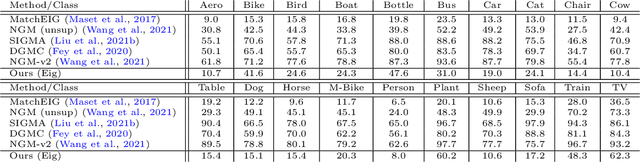
Abstract:Multigraph matching is a recent variant of the graph matching problem. In this framework, the optimization procedure considers several graphs and enforces the consistency of the matches along the graphs. This constraint can be formalized as a cycle consistency across the pairwise permutation matrices, which implies the definition of a universe of vertex~\citep{pachauri2013solving}. The label of each vertex is encoded by a sparse vector and the dimension of this space corresponds to the rank of the bulk permutation matrix, the matrix built from the aggregation of all the pairwise permutation matrices. The matching problem can then be formulated as a non-convex quadratic optimization problem (QAP) under constraints imposed on the rank and the permutations. In this paper, we introduce a novel kernelized multigraph matching technique that handles vectors of attributes on both the vertices and edges of the graphs, while maintaining a low memory usage. We solve the QAP problem using a projected power optimization approach and propose several projectors leading to improved stability of the results. We provide several experiments showing that our method is competitive against other unsupervised methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge