Tackling the Matrix Multiplication Micro-kernel Generation with Exo

The optimization of the matrix multiplication (or GEMM) has been a need during the last decades. This operation is considered the flagship of current linear algebra libraries such as BLIS, OpenBLAS, or Intel OneAPI because of its widespread use in a large variety of scientific applications. The GEMM is usually implemented following the GotoBLAS philosophy, which tiles the GEMM operands and uses a series of nested loops for performance improvement. These approaches extract the maximum computational power of the architectures through small pieces of hardware-oriented, high-performance code called micro-kernel. However, this approach forces developers to generate, with a non-negligible effort, a dedicated micro-kernel for each new hardware. In this work, we present a step-by-step procedure for generating micro-kernels with the Exo compiler that performs close to (or even better than) manually developed microkernels written with intrinsic functions or assembly language. Our solution also improves the portability of the generated code, since a hardware target is fully specified by a concise library-based description of its instructions.

Full Stack Optimization of Transformer Inference: a Survey

Recent advances in state-of-the-art DNN architecture design have been moving toward Transformer models. These models achieve superior accuracy across a wide range of applications. This trend has been consistent over the past several years since Transformer models were originally introduced. However, the amount of compute and bandwidth required for inference of recent Transformer models is growing at a significant rate, and this has made their deployment in latency-sensitive applications challenging. As such, there has been an increased focus on making Transformer models more efficient, with methods that range from changing the architecture design, all the way to developing dedicated domain-specific accelerators. In this work, we survey different approaches for efficient Transformer inference, including: (i) analysis and profiling of the bottlenecks in existing Transformer architectures and their similarities and differences with previous convolutional models; (ii) implications of Transformer architecture on hardware, including the impact of non-linear operations such as Layer Normalization, Softmax, and GELU, as well as linear operations, on hardware design; (iii) approaches for optimizing a fixed Transformer architecture; (iv) challenges in finding the right mapping and scheduling of operations for Transformer models; and (v) approaches for optimizing Transformer models by adapting the architecture using neural architecture search. Finally, we perform a case study by applying the surveyed optimizations on Gemmini, the open-source, full-stack DNN accelerator generator, and we show how each of these approaches can yield improvements, compared to previous benchmark results on Gemmini. Among other things, we find that a full-stack co-design approach with the aforementioned methods can result in up to 88.7x speedup with a minimal performance degradation for Transformer inference.

CoSA: Scheduling by Constrained Optimization for Spatial Accelerators

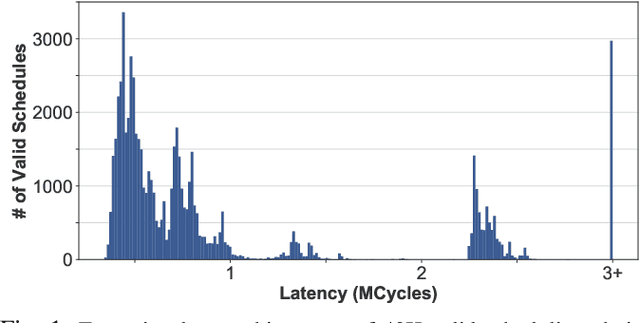
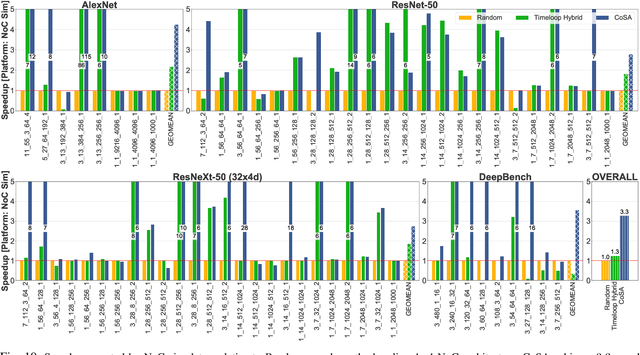
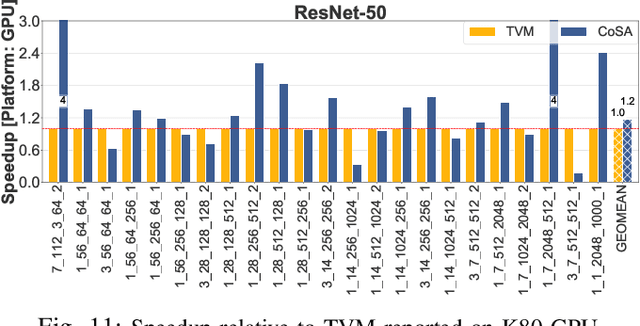
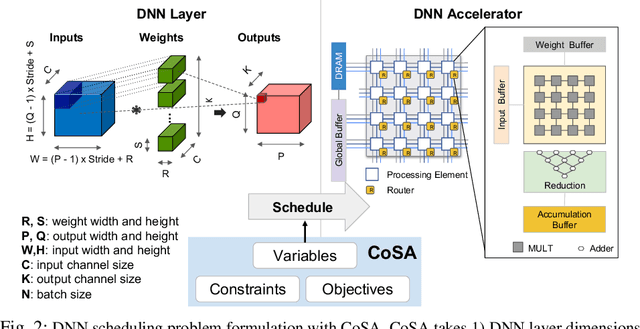
Recent advances in Deep Neural Networks (DNNs) have led to active development of specialized DNN accelerators, many of which feature a large number of processing elements laid out spatially, together with a multi-level memory hierarchy and flexible interconnect. While DNN accelerators can take advantage of data reuse and achieve high peak throughput, they also expose a large number of runtime parameters to the programmers who need to explicitly manage how computation is scheduled both spatially and temporally. In fact, different scheduling choices can lead to wide variations in performance and efficiency, motivating the need for a fast and efficient search strategy to navigate the vast scheduling space. To address this challenge, we present CoSA, a constrained-optimization-based approach for scheduling DNN accelerators. As opposed to existing approaches that either rely on designers' heuristics or iterative methods to navigate the search space, CoSA expresses scheduling decisions as a constrained-optimization problem that can be deterministically solved using mathematical optimization techniques. Specifically, CoSA leverages the regularities in DNN operators and hardware to formulate the DNN scheduling space into a mixed-integer programming (MIP) problem with algorithmic and architectural constraints, which can be solved to automatically generate a highly efficient schedule in one shot. We demonstrate that CoSA-generated schedules significantly outperform state-of-the-art approaches by a geometric mean of up to 2.5x across a wide range of DNN networks while improving the time-to-solution by 90x.