ADMM for Structured Fractional Minimization

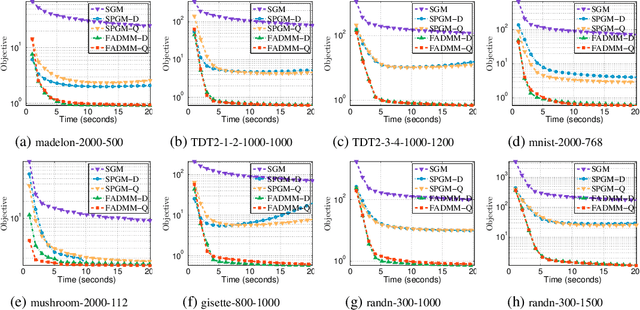
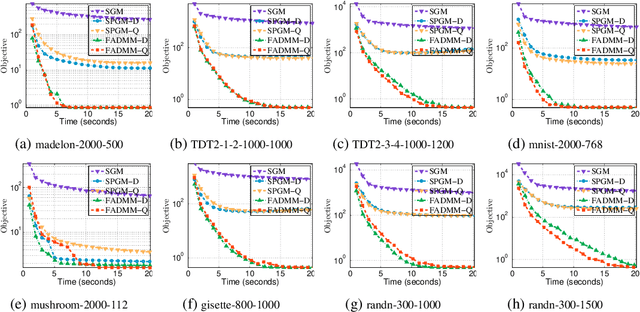
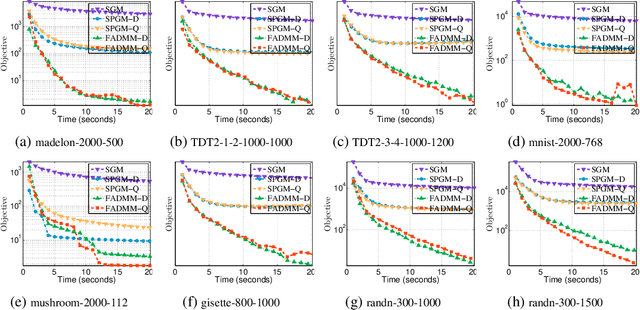
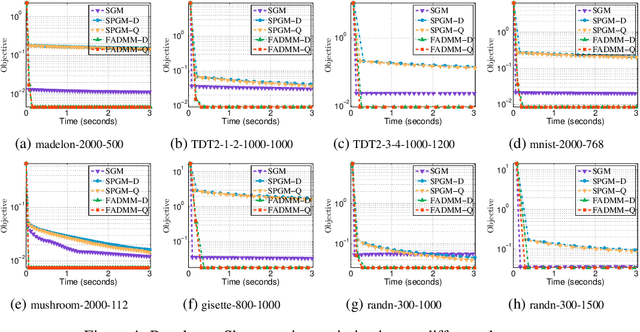
We consider a class of structured fractional minimization problems, where the numerator includes a differentiable function, a simple nonconvex nonsmooth function, a concave nonsmooth function, and a convex nonsmooth function composed with a linear operator, while the denominator is a continuous function that is either weakly convex or has a weakly convex square root. These problems are widespread and span numerous essential applications in machine learning and data science. Existing methods are mainly based on subgradient methods and smoothing proximal gradient methods, which may suffer from slow convergence and numerical stability issues. In this paper, we introduce {\sf FADMM}, the first Alternating Direction Method of Multipliers tailored for this class of problems. {\sf FADMM} decouples the original problem into linearized proximal subproblems, featuring two variants: one using Dinkelbach's parametric method ({\sf FADMM-D}) and the other using the quadratic transform method ({\sf FADMM-Q}). By introducing a novel Lyapunov function, we establish that {\sf FADMM} converges to $\epsilon$-approximate critical points of the problem within an oracle complexity of $\mathcal{O}(1/\epsilon^{3})$. Our experiments on synthetic and real-world data for sparse Fisher discriminant analysis, robust Sharpe ratio minimization, and robust sparse recovery demonstrate the effectiveness of our approach. Keywords: Fractional Minimization, Nonconvex Optimization, Proximal Linearized ADMM, Nonsmooth Optimization, Convergence Analysis

A Block Coordinate Descent Method for Nonsmooth Composite Optimization under Orthogonality Constraints

Nonsmooth composite optimization with orthogonality constraints has a broad spectrum of applications in statistical learning and data science. However, this problem is generally challenging to solve due to its non-convex and non-smooth nature. Existing solutions are limited by one or more of the following restrictions: (i) they are full gradient methods that require high computational costs in each iteration; (ii) they are not capable of solving general nonsmooth composite problems; (iii) they are infeasible methods and can only achieve the feasibility of the solution at the limit point; (iv) they lack rigorous convergence guarantees; (v) they only obtain weak optimality of critical points. In this paper, we propose \textit{\textbf{OBCD}}, a new Block Coordinate Descent method for solving general nonsmooth composite problems under Orthogonality constraints. \textit{\textbf{OBCD}} is a feasible method with low computation complexity footprints. In each iteration, our algorithm updates $k$ rows of the solution matrix ($k\geq2$ is a parameter) to preserve the constraints. Then, it solves a small-sized nonsmooth composite optimization problem under orthogonality constraints either exactly or approximately. We demonstrate that any exact block-$k$ stationary point is always an approximate block-$k$ stationary point, which is equivalent to the critical stationary point. We are particularly interested in the case where $k=2$ as the resulting subproblem reduces to a one-dimensional nonconvex problem. We propose a breakpoint searching method and a fifth-order iterative method to solve this problem efficiently and effectively. We also propose two novel greedy strategies to find a good working set to further accelerate the convergence of \textit{\textbf{OBCD}}. Finally, we have conducted extensive experiments on several tasks to demonstrate the superiority of our approach.

Coordinate Descent Methods for Fractional Minimization

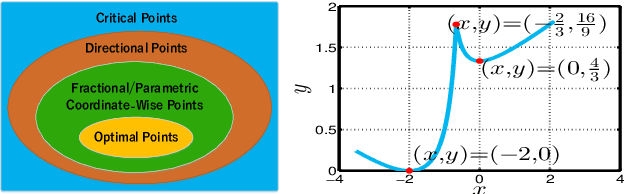
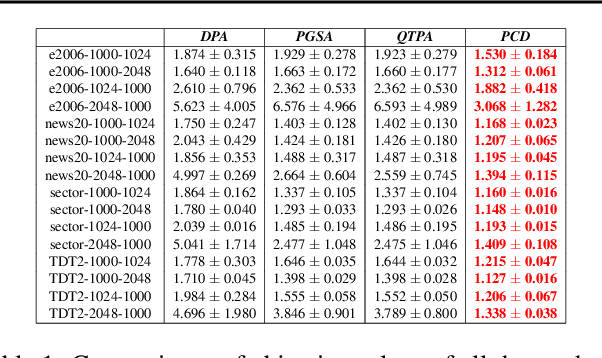
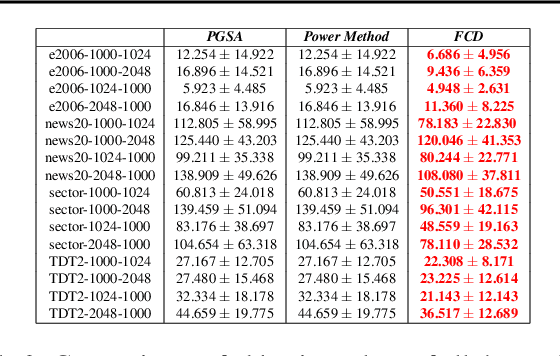
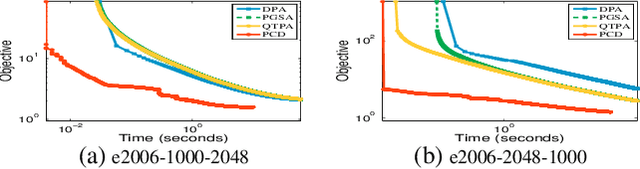
We consider a class of structured fractional minimization problems, in which the numerator part of the objective is the sum of a differentiable convex function and a convex nonsmooth function, while the denominator part is a concave or convex function. This problem is difficult to solve since it is nonconvex. By exploiting the structure of the problem, we propose two Coordinate Descent (CD) methods for solving this problem. One is applied to the original fractional function, the other is based on the associated parametric problem. The proposed methods iteratively solve a one-dimensional subproblem \textit{globally}, and they are guaranteed to converge to coordinate-wise stationary points. In the case of a convex denominator, we prove that the proposed CD methods using sequential nonconvex approximation find stronger stationary points than existing methods. Under suitable conditions, CD methods with an appropriate initialization converge linearly to the optimal point (also the coordinate-wise stationary point). In the case of a concave denominator, we show that the resulting problem is quasi-convex, and any critical point is a global minimum. We prove that the algorithms converge to the global optimal solution with a sublinear convergence rate. We demonstrate the applicability of the proposed methods to some machine learning and signal processing models. Our experiments on real-world data have shown that our method significantly and consistently outperforms existing methods in terms of accuracy.

Coordinate Descent Methods for DC Minimization

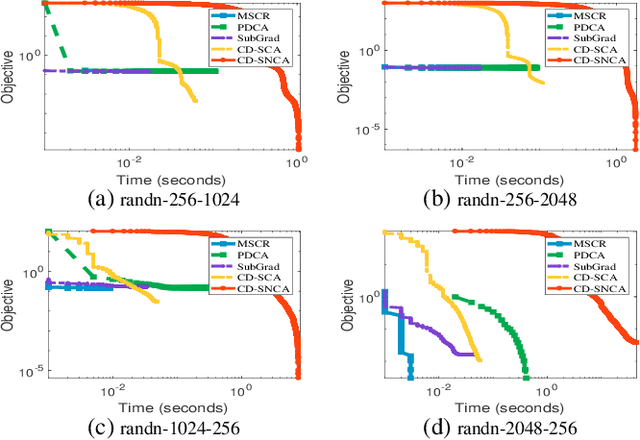
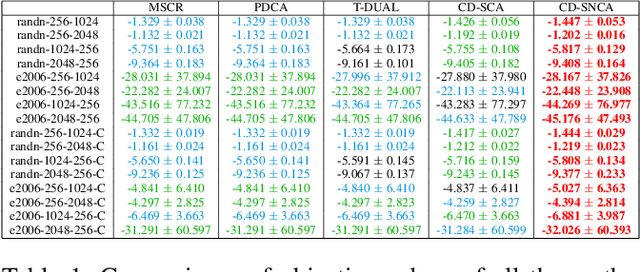
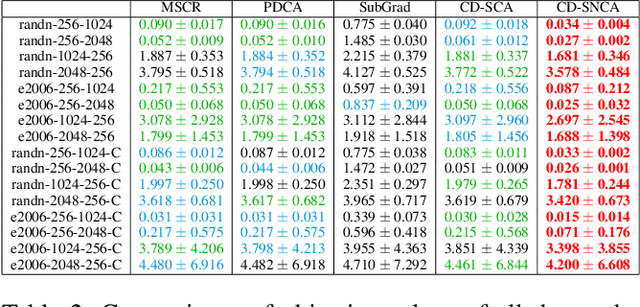
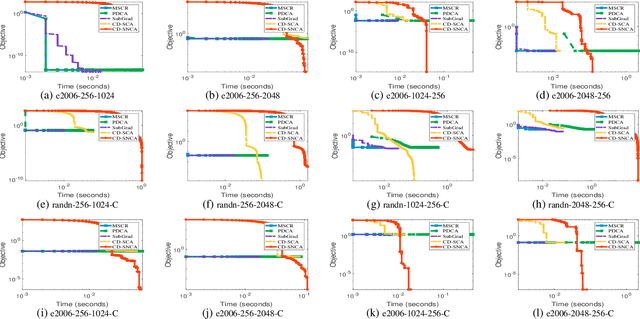
Difference-of-Convex (DC) minimization, referring to the problem of minimizing the difference of two convex functions, has been found rich applications in statistical learning and studied extensively for decades. However, existing methods are primarily based on multi-stage convex relaxation, only leading to weak optimality of critical points. This paper proposes a coordinate descent method for minimizing DC functions based on sequential nonconvex approximation. Our approach iteratively solves a nonconvex one-dimensional subproblem globally, and it is guaranteed to converge to a coordinate-wise stationary point. We prove that this new optimality condition is always stronger than the critical point condition and the directional point condition when the objective function is weakly convex. For comparisons, we also include a naive variant of coordinate descent methods based on sequential convex approximation in our study. When the objective function satisfies an additional regularity condition called \emph{sharpness}, coordinate descent methods with an appropriate initialization converge \emph{linearly} to the optimal solution set. Also, for many applications of interest, we show that the nonconvex one-dimensional subproblem can be computed exactly and efficiently using a breakpoint searching method. We present some discussions and extensions of our proposed method. Finally, we have conducted extensive experiments on several statistical learning tasks to show the superiority of our approach. Keywords: Coordinate Descent, DC Minimization, DC Programming, Difference-of-Convex Programs, Nonconvex Optimization, Sparse Optimization, Binary Optimization.

A Coordinate-wise Optimization Algorithm for Sparse Inverse Covariance Selection

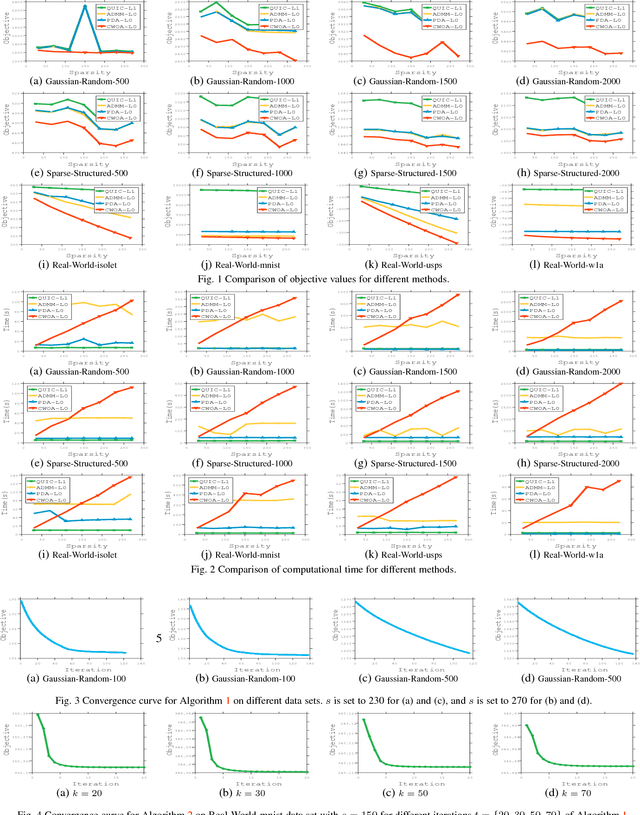
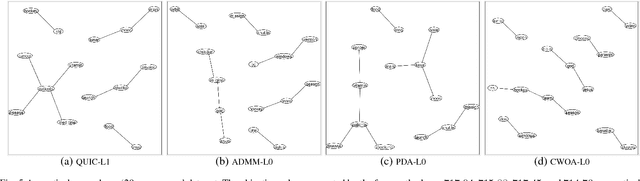
Sparse inverse covariance selection is a fundamental problem for analyzing dependencies in high dimensional data. However, such a problem is difficult to solve since it is NP-hard. Existing solutions are primarily based on convex approximation and iterative hard thresholding, which only lead to sub-optimal solutions. In this work, we propose a coordinate-wise optimization algorithm to solve this problem which is guaranteed to converge to a coordinate-wise minimum point. The algorithm iteratively and greedily selects one variable or swaps two variables to identify the support set, and then solves a reduced convex optimization problem over the support set to achieve the greatest descent. As a side contribution of this paper, we propose a Newton-like algorithm to solve the reduced convex sub-problem, which is proven to always converge to the optimal solution with global linear convergence rate and local quadratic convergence rate. Finally, we demonstrate the efficacy of our method on synthetic data and real-world data sets. As a result, the proposed method consistently outperforms existing solutions in terms of accuracy.

Convex Optimization for Linear Query Processing under Approximate Differential Privacy

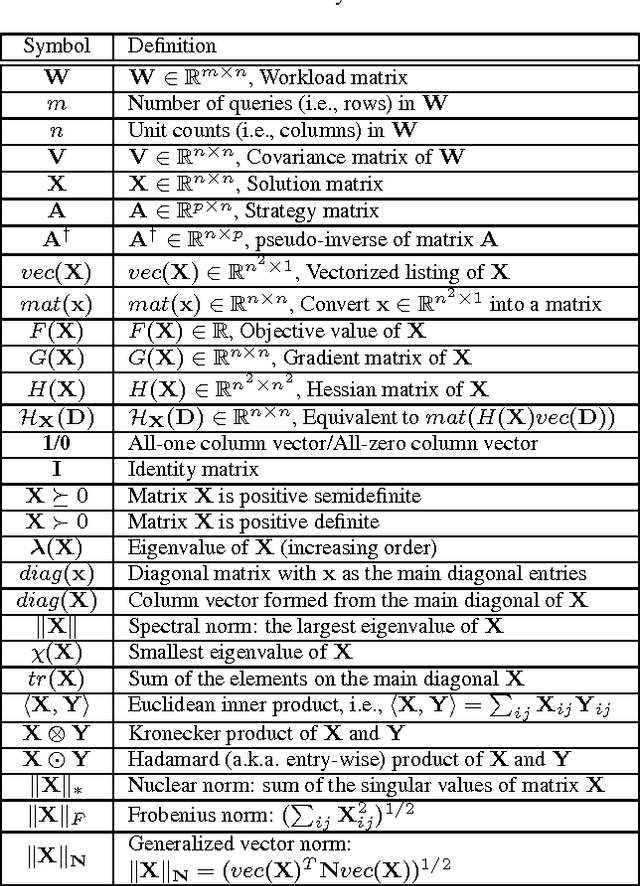
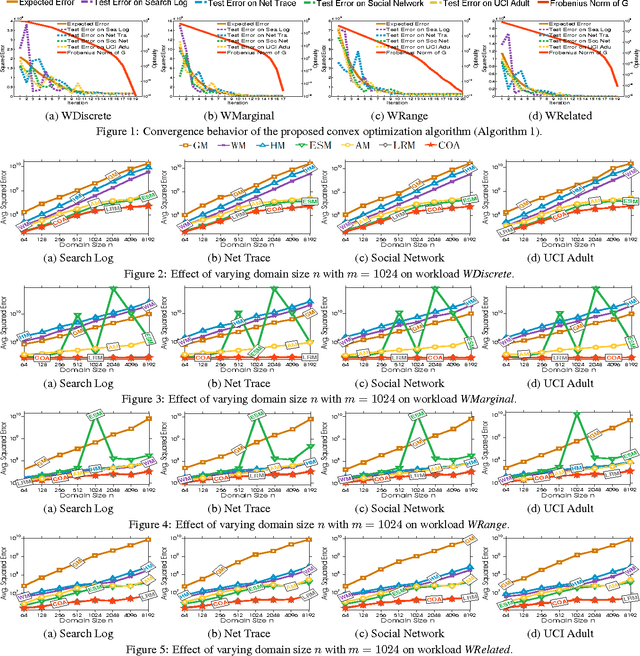
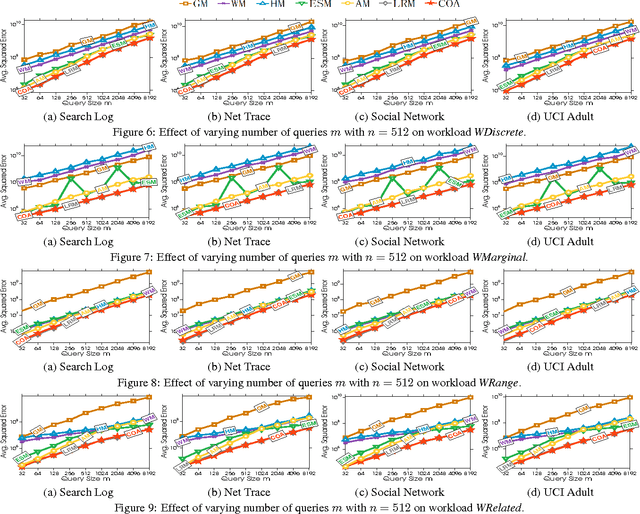
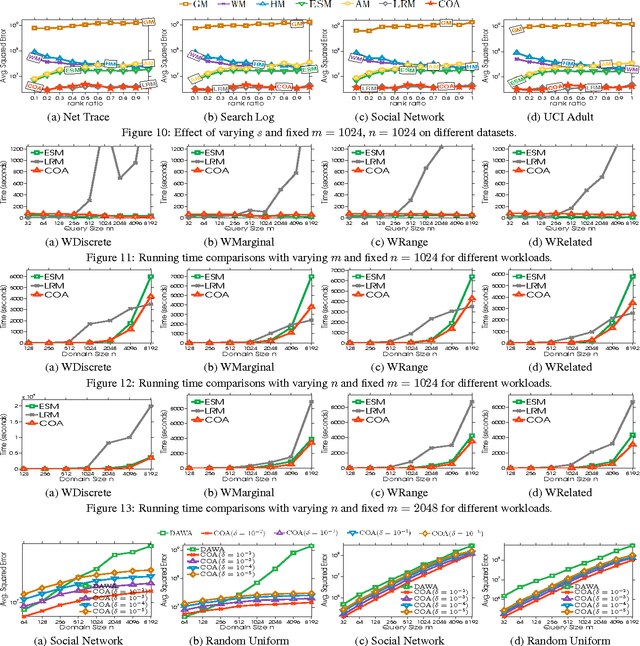
Differential privacy enables organizations to collect accurate aggregates over sensitive data with strong, rigorous guarantees on individuals' privacy. Previous work has found that under differential privacy, computing multiple correlated aggregates as a batch, using an appropriate \emph{strategy}, may yield higher accuracy than computing each of them independently. However, finding the best strategy that maximizes result accuracy is non-trivial, as it involves solving a complex constrained optimization program that appears to be non-linear and non-convex. Hence, in the past much effort has been devoted in solving this non-convex optimization program. Existing approaches include various sophisticated heuristics and expensive numerical solutions. None of them, however, guarantees to find the optimal solution of this optimization problem. This paper points out that under ($\epsilon$, $\delta$)-differential privacy, the optimal solution of the above constrained optimization problem in search of a suitable strategy can be found, rather surprisingly, by solving a simple and elegant convex optimization program. Then, we propose an efficient algorithm based on Newton's method, which we prove to always converge to the optimal solution with linear global convergence rate and quadratic local convergence rate. Empirical evaluations demonstrate the accuracy and efficiency of the proposed solution.