Convex Optimization for Linear Query Processing under Approximate Differential Privacy
Paper and Code
May 16, 2016
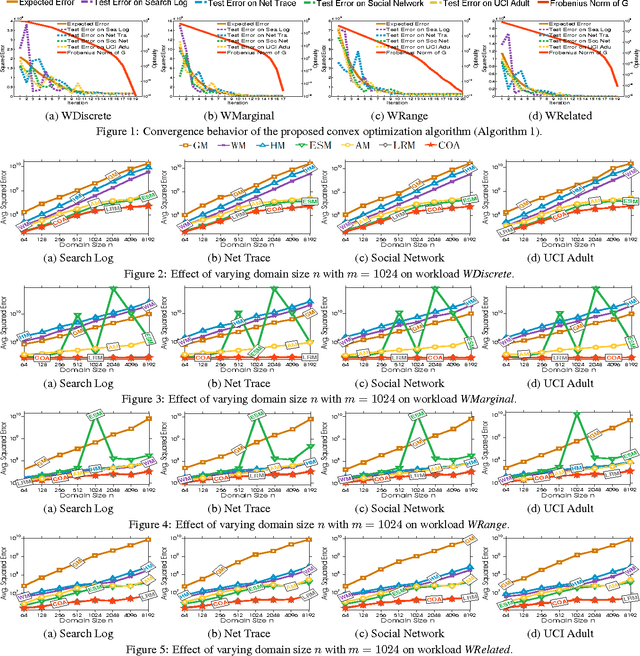
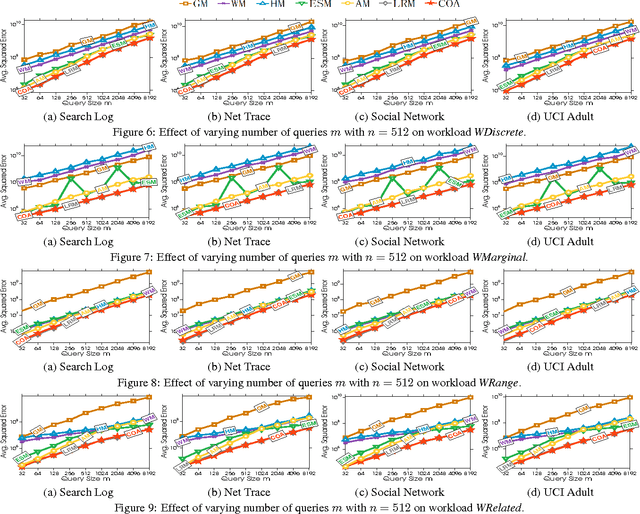
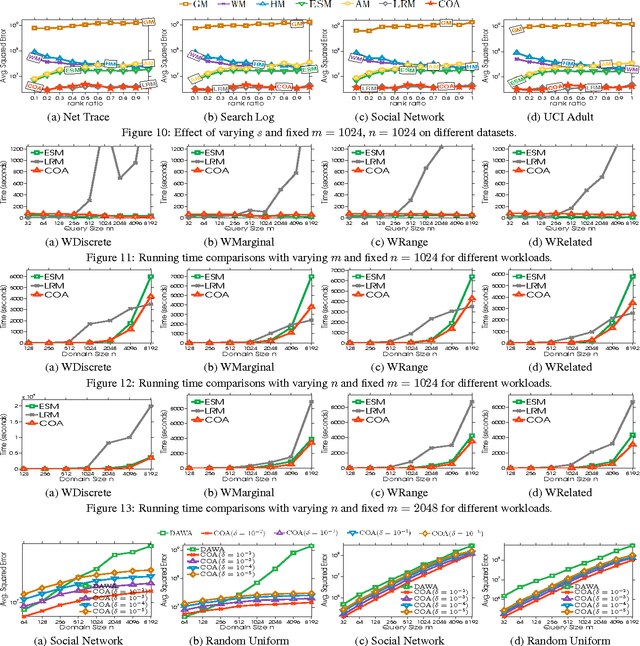
Differential privacy enables organizations to collect accurate aggregates over sensitive data with strong, rigorous guarantees on individuals' privacy. Previous work has found that under differential privacy, computing multiple correlated aggregates as a batch, using an appropriate \emph{strategy}, may yield higher accuracy than computing each of them independently. However, finding the best strategy that maximizes result accuracy is non-trivial, as it involves solving a complex constrained optimization program that appears to be non-linear and non-convex. Hence, in the past much effort has been devoted in solving this non-convex optimization program. Existing approaches include various sophisticated heuristics and expensive numerical solutions. None of them, however, guarantees to find the optimal solution of this optimization problem. This paper points out that under ($\epsilon$, $\delta$)-differential privacy, the optimal solution of the above constrained optimization problem in search of a suitable strategy can be found, rather surprisingly, by solving a simple and elegant convex optimization program. Then, we propose an efficient algorithm based on Newton's method, which we prove to always converge to the optimal solution with linear global convergence rate and quadratic local convergence rate. Empirical evaluations demonstrate the accuracy and efficiency of the proposed solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge