A Coordinate-wise Optimization Algorithm for Sparse Inverse Covariance Selection
Paper and Code
Apr 04, 2018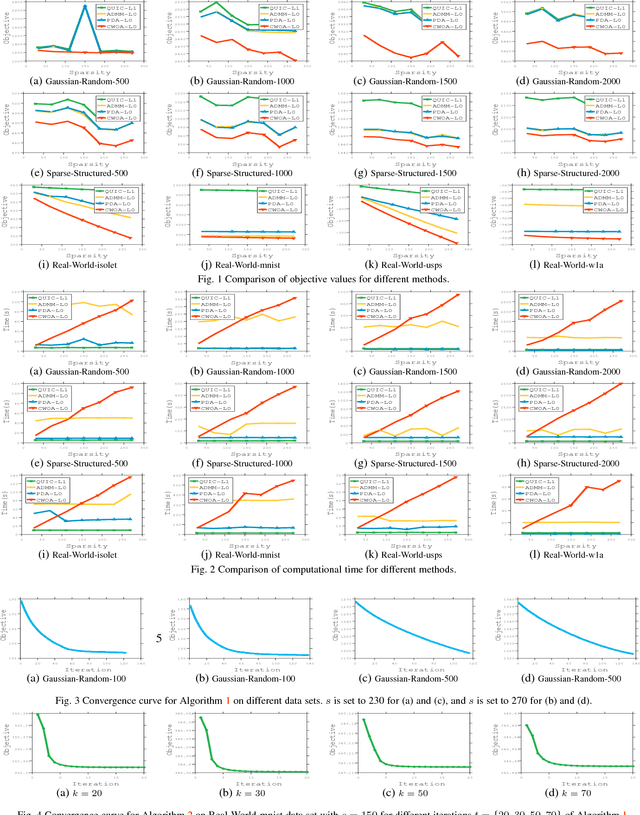
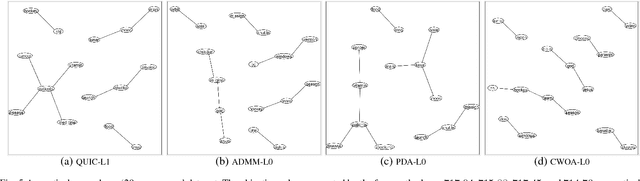
Sparse inverse covariance selection is a fundamental problem for analyzing dependencies in high dimensional data. However, such a problem is difficult to solve since it is NP-hard. Existing solutions are primarily based on convex approximation and iterative hard thresholding, which only lead to sub-optimal solutions. In this work, we propose a coordinate-wise optimization algorithm to solve this problem which is guaranteed to converge to a coordinate-wise minimum point. The algorithm iteratively and greedily selects one variable or swaps two variables to identify the support set, and then solves a reduced convex optimization problem over the support set to achieve the greatest descent. As a side contribution of this paper, we propose a Newton-like algorithm to solve the reduced convex sub-problem, which is proven to always converge to the optimal solution with global linear convergence rate and local quadratic convergence rate. Finally, we demonstrate the efficacy of our method on synthetic data and real-world data sets. As a result, the proposed method consistently outperforms existing solutions in terms of accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge