On scientific understanding with artificial intelligence

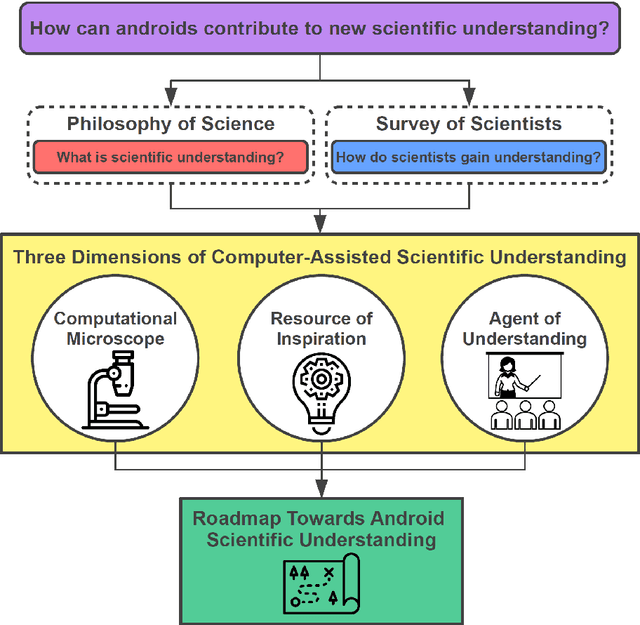
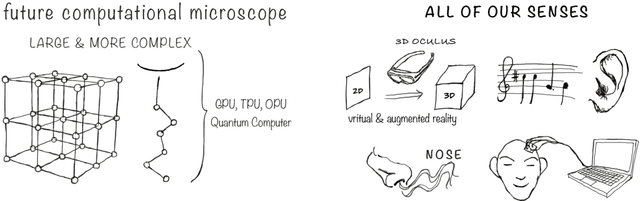
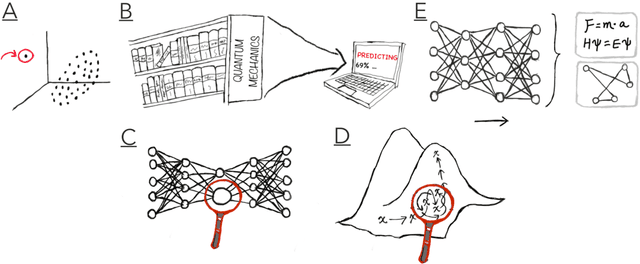
Imagine an oracle that correctly predicts the outcome of every particle physics experiment, the products of every chemical reaction, or the function of every protein. Such an oracle would revolutionize science and technology as we know them. However, as scientists, we would not be satisfied with the oracle itself. We want more. We want to comprehend how the oracle conceived these predictions. This feat, denoted as scientific understanding, has frequently been recognized as the essential aim of science. Now, the ever-growing power of computers and artificial intelligence poses one ultimate question: How can advanced artificial systems contribute to scientific understanding or achieve it autonomously? We are convinced that this is not a mere technical question but lies at the core of science. Therefore, here we set out to answer where we are and where we can go from here. We first seek advice from the philosophy of science to understand scientific understanding. Then we review the current state of the art, both from literature and by collecting dozens of anecdotes from scientists about how they acquired new conceptual understanding with the help of computers. Those combined insights help us to define three dimensions of android-assisted scientific understanding: The android as a I) computational microscope, II) resource of inspiration and the ultimate, not yet existent III) agent of understanding. For each dimension, we explain new avenues to push beyond the status quo and unleash the full power of artificial intelligence's contribution to the central aim of science. We hope our perspective inspires and focuses research towards androids that get new scientific understanding and ultimately bring us closer to true artificial scientists.

Bayesian optimization with known experimental and design constraints for chemistry applications

Optimization strategies driven by machine learning, such as Bayesian optimization, are being explored across experimental sciences as an efficient alternative to traditional design of experiment. When combined with automated laboratory hardware and high-performance computing, these strategies enable next-generation platforms for autonomous experimentation. However, the practical application of these approaches is hampered by a lack of flexible software and algorithms tailored to the unique requirements of chemical research. One such aspect is the pervasive presence of constraints in the experimental conditions when optimizing chemical processes or protocols, and in the chemical space that is accessible when designing functional molecules or materials. Although many of these constraints are known a priori, they can be interdependent, non-linear, and result in non-compact optimization domains. In this work, we extend our experiment planning algorithms Phoenics and Gryffin such that they can handle arbitrary known constraints via an intuitive and flexible interface. We benchmark these extended algorithms on continuous and discrete test functions with a diverse set of constraints, demonstrating their flexibility and robustness. In addition, we illustrate their practical utility in two simulated chemical research scenarios: the optimization of the synthesis of o-xylenyl Buckminsterfullerene adducts under constrained flow conditions, and the design of redox active molecules for flow batteries under synthetic accessibility constraints. The tools developed constitute a simple, yet versatile strategy to enable model-based optimization with known experimental constraints, contributing to its applicability as a core component of autonomous platforms for scientific discovery.

Golem: An algorithm for robust experiment and process optimization

Numerous challenges in science and engineering can be framed as optimization tasks, including the maximization of reaction yields, the optimization of molecular and materials properties, and the fine-tuning of automated hardware protocols. Design of experiment and optimization algorithms are often adopted to solve these tasks efficiently. Increasingly, these experiment planning strategies are coupled with automated hardware to enable autonomous experimental platforms. The vast majority of the strategies used, however, do not consider robustness against the variability of experiment and process conditions. In fact, it is generally assumed that these parameters are exact and reproducible. Yet some experiments may have considerable noise associated with some of their conditions, and process parameters optimized under precise control may be applied in the future under variable operating conditions. In either scenario, the optimal solutions found might not be robust against input variability, affecting the reproducibility of results and returning suboptimal performance in practice. Here, we introduce Golem, an algorithm that is agnostic to the choice of experiment planning strategy and that enables robust experiment and process optimization. Golem identifies optimal solutions that are robust to input uncertainty, thus ensuring the reproducible performance of optimized experimental protocols and processes. It can be used to analyze the robustness of past experiments, or to guide experiment planning algorithms toward robust solutions on the fly. We assess the performance and domain of applicability of Golem through extensive benchmark studies and demonstrate its practical relevance by optimizing an analytical chemistry protocol under the presence of significant noise in its experimental conditions.

Gemini: Dynamic Bias Correction for Autonomous Experimentation and Molecular Simulation

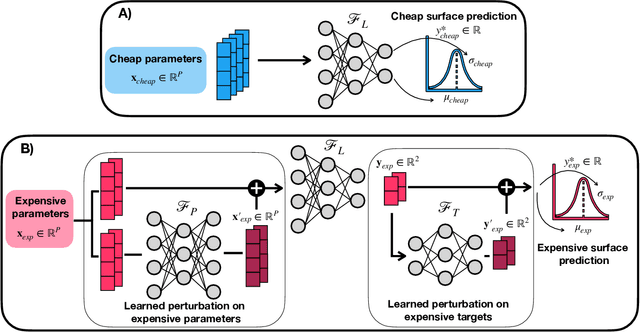
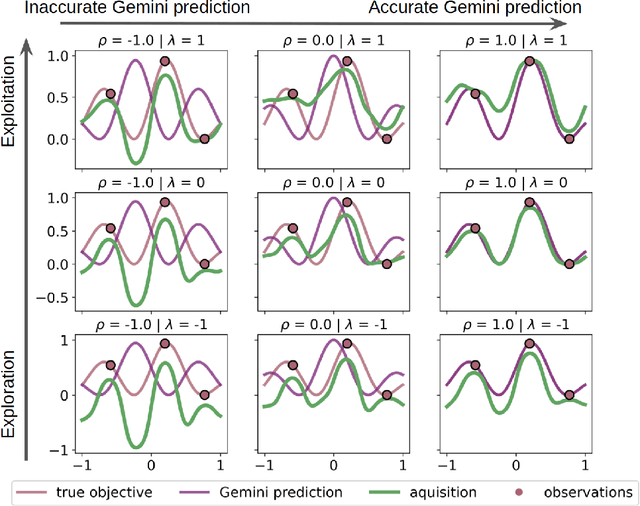
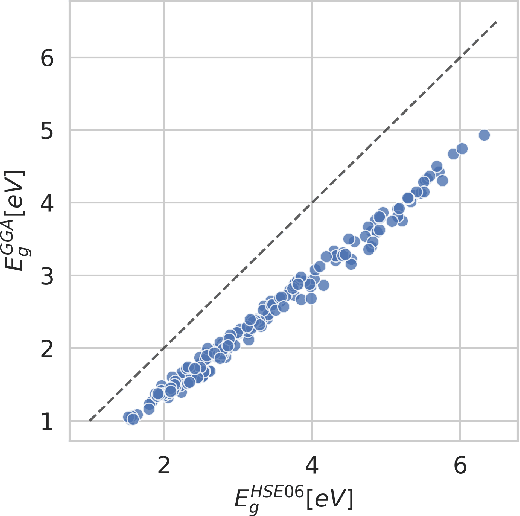
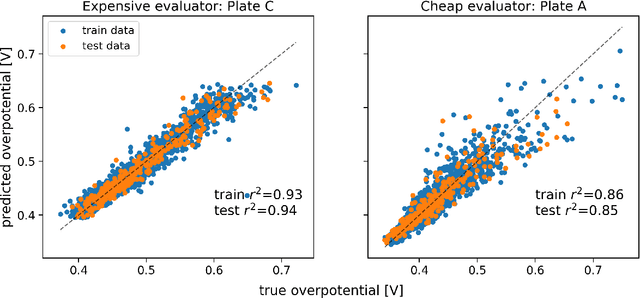
Bayesian optimization has emerged as a powerful strategy to accelerate scientific discovery by means of autonomous experimentation. However, expensive measurements are required to accurately estimate materials properties, and can quickly become a hindrance to exhaustive materials discovery campaigns. Here, we introduce Gemini: a data-driven model capable of using inexpensive measurements as proxies for expensive measurements by correcting systematic biases between property evaluation methods. We recommend using Gemini for regression tasks with sparse data and in an autonomous workflow setting where its predictions of expensive to evaluate objectives can be used to construct a more informative acquisition function, thus reducing the number of expensive evaluations an optimizer needs to achieve desired target values. In a regression setting, we showcase the ability of our method to make accurate predictions of DFT calculated bandgaps of hybrid organic-inorganic perovskite materials. We further demonstrate the benefits that Gemini provides to autonomous workflows by augmenting the Bayesian optimizer Phoenics to yeild a scalable optimization framework leveraging multiple sources of measurement. Finally, we simulate an autonomous materials discovery platform for optimizing the activity of electrocatalysts for the oxygen evolution reaction. Realizing autonomous workflows with Gemini, we show that the number of measurements of a composition space comprising expensive and rare metals needed to achieve a target overpotential is significantly reduced when measurements from a proxy composition system with less expensive metals are available.

Olympus: a benchmarking framework for noisy optimization and experiment planning

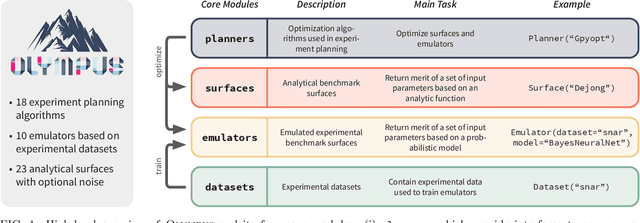
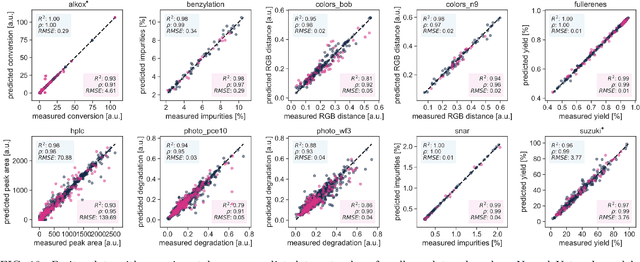
Research challenges encountered across science, engineering, and economics can frequently be formulated as optimization tasks. In chemistry and materials science, recent growth in laboratory digitization and automation has sparked interest in optimization-guided autonomous discovery and closed-loop experimentation. Experiment planning strategies based on off-the-shelf optimization algorithms can be employed in fully autonomous research platforms to achieve desired experimentation goals with the minimum number of trials. However, the experiment planning strategy that is most suitable to a scientific discovery task is a priori unknown while rigorous comparisons of different strategies are highly time and resource demanding. As optimization algorithms are typically benchmarked on low-dimensional synthetic functions, it is unclear how their performance would translate to noisy, higher-dimensional experimental tasks encountered in chemistry and materials science. We introduce Olympus, a software package that provides a consistent and easy-to-use framework for benchmarking optimization algorithms against realistic experiments emulated via probabilistic deep-learning models. Olympus includes a collection of experimentally derived benchmark sets from chemistry and materials science and a suite of experiment planning strategies that can be easily accessed via a user-friendly python interface. Furthermore, Olympus facilitates the integration, testing, and sharing of custom algorithms and user-defined datasets. In brief, Olympus mitigates the barriers associated with benchmarking optimization algorithms on realistic experimental scenarios, promoting data sharing and the creation of a standard framework for evaluating the performance of experiment planning strategies

Gryffin: An algorithm for Bayesian optimization for categorical variables informed by physical intuition with applications to chemistry

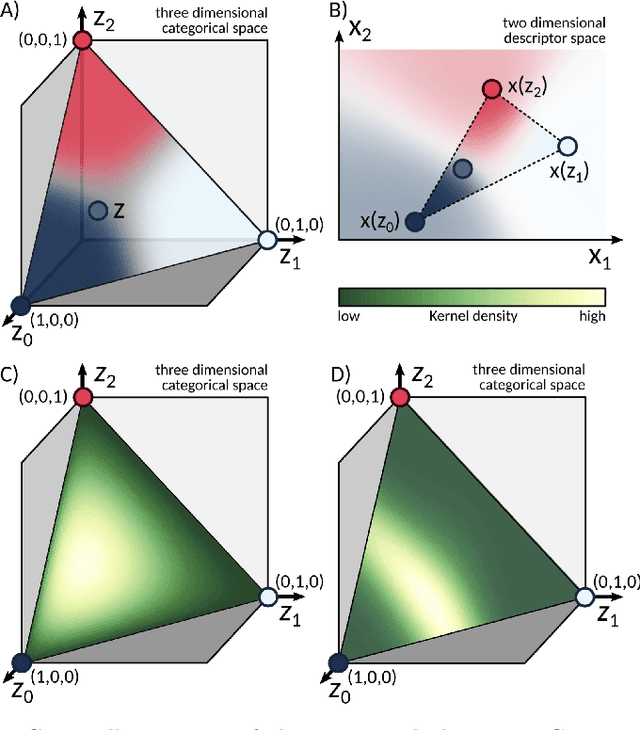
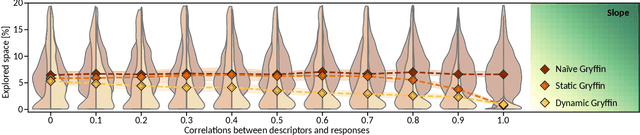
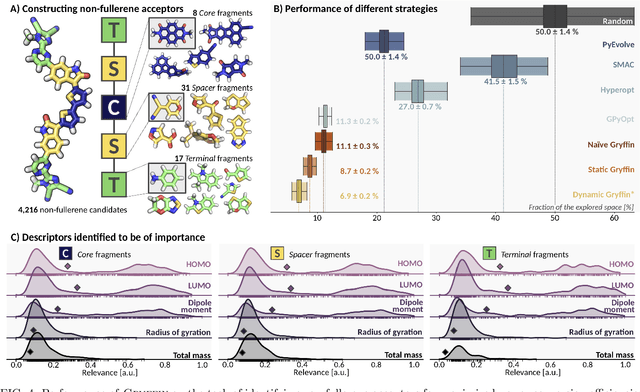
Designing functional molecules and advanced materials requires complex interdependent design choices: tuning continuous process parameters such as temperatures or flow rates, while simultaneously selecting categorical variables like catalysts or solvents. To date, the development of data-driven experiment planning strategies for autonomous experimentation has largely focused on continuous process parameters despite the urge to devise efficient strategies for the selection of categorical variables to substantially accelerate scientific discovery. We introduce Gryffin, as a general purpose optimization framework for the autonomous selection of categorical variables driven by expert knowledge. Gryffin augments Bayesian optimization with kernel density estimation using smooth approximations to categorical distributions. Leveraging domain knowledge from physicochemical descriptors to characterize categorical options, Gryffin can significantly accelerate the search for promising molecules and materials. Gryffin can further highlight relevant correlations between the provided descriptors to inspire physical insights and foster scientific intuition. In addition to comprehensive benchmarks, we demonstrate the capabilities and performance of Gryffin on three examples in materials science and chemistry: (i) the discovery of non-fullerene acceptors for organic solar cells, (ii) the design of hybrid organic-inorganic perovskites for light-harvesting, and (iii) the identification of ligands and process parameters for Suzuki-Miyaura reactions. Our observations suggest that Gryffin, in its simplest form without descriptors, constitutes a competitive categorical optimizer compared to state-of-the-art approaches. However, when leveraging domain knowledge provided via descriptors, Gryffin can optimize at considerable higher rates and refine this domain knowledge to spark scientific understanding.

SELFIES: a robust representation of semantically constrained graphs with an example application in chemistry

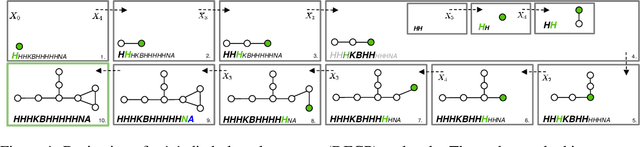
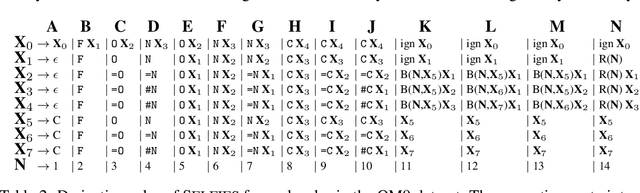
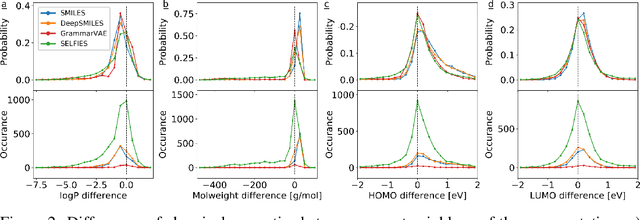
Graphs are ideal representations of complex, relational information. Their applications span diverse areas of science and engineering, such as Feynman diagrams in fundamental physics, the structures of molecules in chemistry or transport systems in urban planning. Recently, many of these examples turned into the spotlight as applications of machine learning (ML). There, common challenges to the successful deployment of ML are domain-specific constraints, which lead to semantically constrained graphs. While much progress has been achieved in the generation of valid graphs for domain- and model-specific applications, a general approach has not been demonstrated yet. Here, we present a general-purpose, sequence-based, robust representation of semantically constrained graphs, which we call SELFIES (SELF-referencIng Embedded Strings). SELFIES are based on a Chomsky type-2 grammar, augmented with two self-referencing functions. We demonstrate their applicability to represent chemical compound structures and compare them to perhaps the most popular 2D representation, SMILES, and other important baselines. We find stronger robustness against character mutations while still maintaining similar chemical properties. Even entirely random SELFIES produce semantically valid graphs in most of the cases. As feature representation in variational autoencoders, SELFIES provide a substantial improvement in the task of in reconstruction, validity, and diversity. We anticipate that SELFIES allow for direct applications in ML, without the need for domain-specific adaptation of model architectures. SELFIES are not limited to the structures of small molecules, and we show how to apply them to two other examples from the sciences: representations of DNA and interaction graphs for quantum mechanical experiments.

PHOENICS: A universal deep Bayesian optimizer

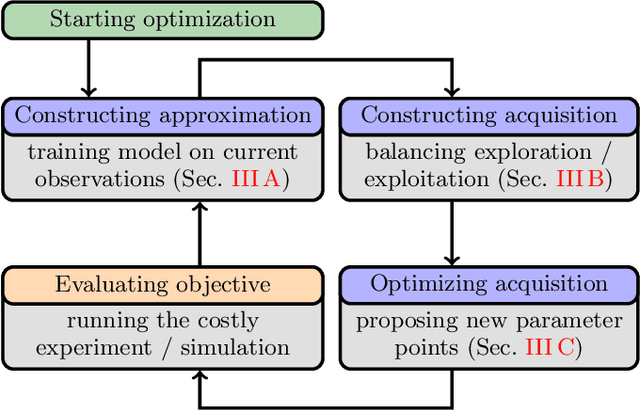
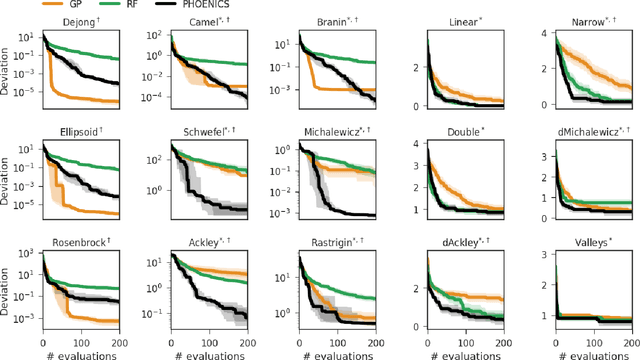
In this work we introduce PHOENICS, a probabilistic global optimization algorithm combining ideas from Bayesian optimization with concepts from Bayesian kernel density estimation. We propose an inexpensive acquisition function balancing the explorative and exploitative behavior of the algorithm. This acquisition function enables intuitive sampling strategies for an efficient parallel search of global minima. The performance of PHOENICS is assessed via an exhaustive benchmark study on a set of 15 discrete, quasi-discrete and continuous multidimensional functions. Unlike optimization methods based on Gaussian processes (GP) and random forests (RF), we show that PHOENICS is less sensitive to the nature of the co-domain, and outperforms GP and RF optimizations. We illustrate the performance of PHOENICS on the Oregonator, a difficult case-study describing a complex chemical reaction network. We demonstrate that only PHOENICS was able to reproduce qualitatively and quantitatively the target dynamic behavior of this nonlinear reaction dynamics. We recommend PHOENICS for rapid optimization of scalar, possibly non-convex, black-box unknown objective functions.

Machine Learning for Quantum Dynamics: Deep Learning of Excitation Energy Transfer Properties

Understanding the relationship between the structure of light-harvesting systems and their excitation energy transfer properties is of fundamental importance in many applications including the development of next generation photovoltaics. Natural light harvesting in photosynthesis shows remarkable excitation energy transfer properties, which suggests that pigment-protein complexes could serve as blueprints for the design of nature inspired devices. Mechanistic insights into energy transport dynamics can be gained by leveraging numerically involved propagation schemes such as the hierarchical equations of motion (HEOM). Solving these equations, however, is computationally costly due to the adverse scaling with the number of pigments. Therefore virtual high-throughput screening, which has become a powerful tool in material discovery, is less readily applicable for the search of novel excitonic devices. We propose the use of artificial neural networks to bypass the computational limitations of established techniques for exploring the structure-dynamics relation in excitonic systems. Once trained, our neural networks reduce computational costs by several orders of magnitudes. Our predicted transfer times and transfer efficiencies exhibit similar or even higher accuracies than frequently used approximate methods such as secular Redfield theory