Gemini: Dynamic Bias Correction for Autonomous Experimentation and Molecular Simulation

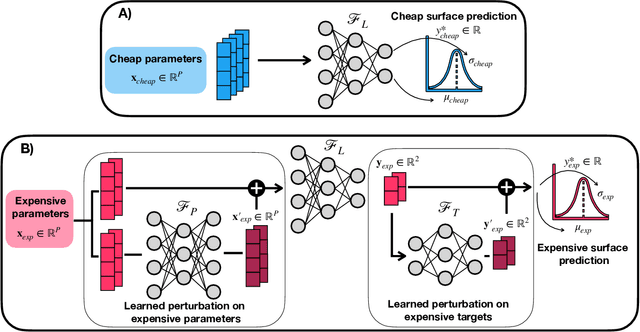
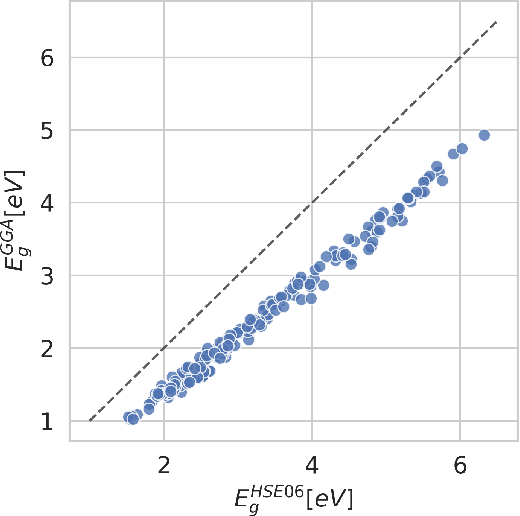
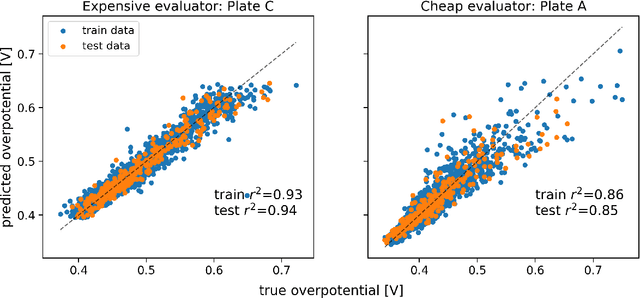
Bayesian optimization has emerged as a powerful strategy to accelerate scientific discovery by means of autonomous experimentation. However, expensive measurements are required to accurately estimate materials properties, and can quickly become a hindrance to exhaustive materials discovery campaigns. Here, we introduce Gemini: a data-driven model capable of using inexpensive measurements as proxies for expensive measurements by correcting systematic biases between property evaluation methods. We recommend using Gemini for regression tasks with sparse data and in an autonomous workflow setting where its predictions of expensive to evaluate objectives can be used to construct a more informative acquisition function, thus reducing the number of expensive evaluations an optimizer needs to achieve desired target values. In a regression setting, we showcase the ability of our method to make accurate predictions of DFT calculated bandgaps of hybrid organic-inorganic perovskite materials. We further demonstrate the benefits that Gemini provides to autonomous workflows by augmenting the Bayesian optimizer Phoenics to yeild a scalable optimization framework leveraging multiple sources of measurement. Finally, we simulate an autonomous materials discovery platform for optimizing the activity of electrocatalysts for the oxygen evolution reaction. Realizing autonomous workflows with Gemini, we show that the number of measurements of a composition space comprising expensive and rare metals needed to achieve a target overpotential is significantly reduced when measurements from a proxy composition system with less expensive metals are available.

Olympus: a benchmarking framework for noisy optimization and experiment planning

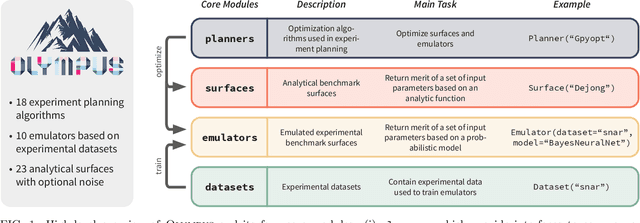
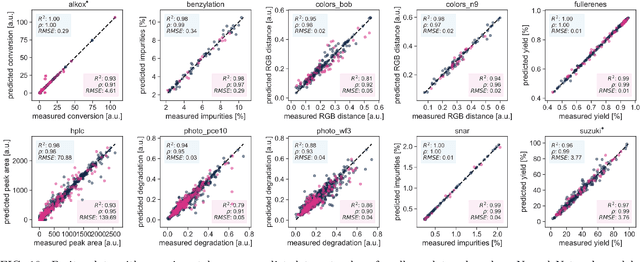
Research challenges encountered across science, engineering, and economics can frequently be formulated as optimization tasks. In chemistry and materials science, recent growth in laboratory digitization and automation has sparked interest in optimization-guided autonomous discovery and closed-loop experimentation. Experiment planning strategies based on off-the-shelf optimization algorithms can be employed in fully autonomous research platforms to achieve desired experimentation goals with the minimum number of trials. However, the experiment planning strategy that is most suitable to a scientific discovery task is a priori unknown while rigorous comparisons of different strategies are highly time and resource demanding. As optimization algorithms are typically benchmarked on low-dimensional synthetic functions, it is unclear how their performance would translate to noisy, higher-dimensional experimental tasks encountered in chemistry and materials science. We introduce Olympus, a software package that provides a consistent and easy-to-use framework for benchmarking optimization algorithms against realistic experiments emulated via probabilistic deep-learning models. Olympus includes a collection of experimentally derived benchmark sets from chemistry and materials science and a suite of experiment planning strategies that can be easily accessed via a user-friendly python interface. Furthermore, Olympus facilitates the integration, testing, and sharing of custom algorithms and user-defined datasets. In brief, Olympus mitigates the barriers associated with benchmarking optimization algorithms on realistic experimental scenarios, promoting data sharing and the creation of a standard framework for evaluating the performance of experiment planning strategies

Gryffin: An algorithm for Bayesian optimization for categorical variables informed by physical intuition with applications to chemistry

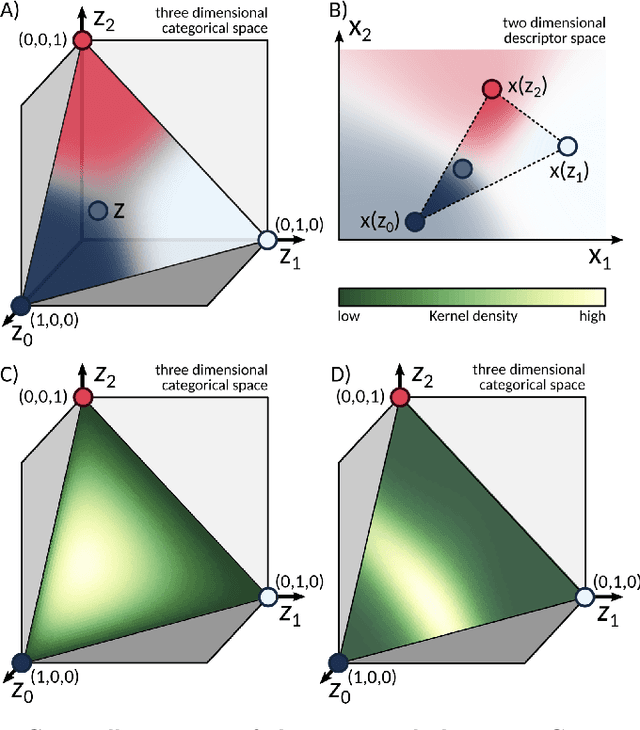
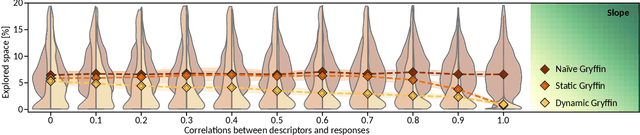
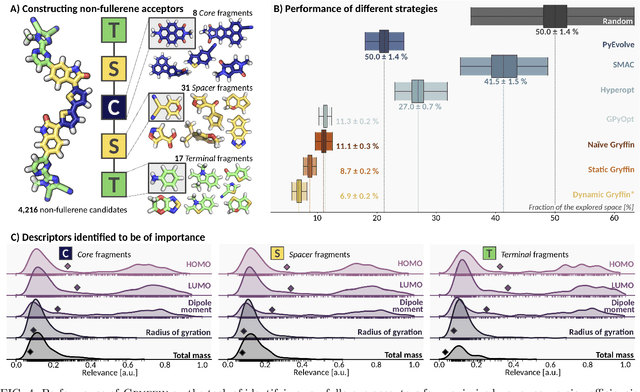
Designing functional molecules and advanced materials requires complex interdependent design choices: tuning continuous process parameters such as temperatures or flow rates, while simultaneously selecting categorical variables like catalysts or solvents. To date, the development of data-driven experiment planning strategies for autonomous experimentation has largely focused on continuous process parameters despite the urge to devise efficient strategies for the selection of categorical variables to substantially accelerate scientific discovery. We introduce Gryffin, as a general purpose optimization framework for the autonomous selection of categorical variables driven by expert knowledge. Gryffin augments Bayesian optimization with kernel density estimation using smooth approximations to categorical distributions. Leveraging domain knowledge from physicochemical descriptors to characterize categorical options, Gryffin can significantly accelerate the search for promising molecules and materials. Gryffin can further highlight relevant correlations between the provided descriptors to inspire physical insights and foster scientific intuition. In addition to comprehensive benchmarks, we demonstrate the capabilities and performance of Gryffin on three examples in materials science and chemistry: (i) the discovery of non-fullerene acceptors for organic solar cells, (ii) the design of hybrid organic-inorganic perovskites for light-harvesting, and (iii) the identification of ligands and process parameters for Suzuki-Miyaura reactions. Our observations suggest that Gryffin, in its simplest form without descriptors, constitutes a competitive categorical optimizer compared to state-of-the-art approaches. However, when leveraging domain knowledge provided via descriptors, Gryffin can optimize at considerable higher rates and refine this domain knowledge to spark scientific understanding.

PHOENICS: A universal deep Bayesian optimizer

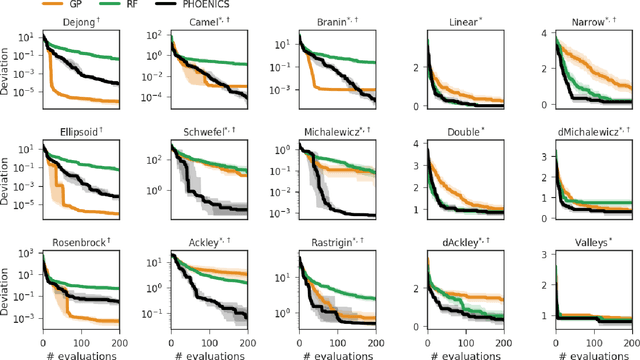
In this work we introduce PHOENICS, a probabilistic global optimization algorithm combining ideas from Bayesian optimization with concepts from Bayesian kernel density estimation. We propose an inexpensive acquisition function balancing the explorative and exploitative behavior of the algorithm. This acquisition function enables intuitive sampling strategies for an efficient parallel search of global minima. The performance of PHOENICS is assessed via an exhaustive benchmark study on a set of 15 discrete, quasi-discrete and continuous multidimensional functions. Unlike optimization methods based on Gaussian processes (GP) and random forests (RF), we show that PHOENICS is less sensitive to the nature of the co-domain, and outperforms GP and RF optimizations. We illustrate the performance of PHOENICS on the Oregonator, a difficult case-study describing a complex chemical reaction network. We demonstrate that only PHOENICS was able to reproduce qualitatively and quantitatively the target dynamic behavior of this nonlinear reaction dynamics. We recommend PHOENICS for rapid optimization of scalar, possibly non-convex, black-box unknown objective functions.