PHOENICS: A universal deep Bayesian optimizer
Paper and Code
Jan 04, 2018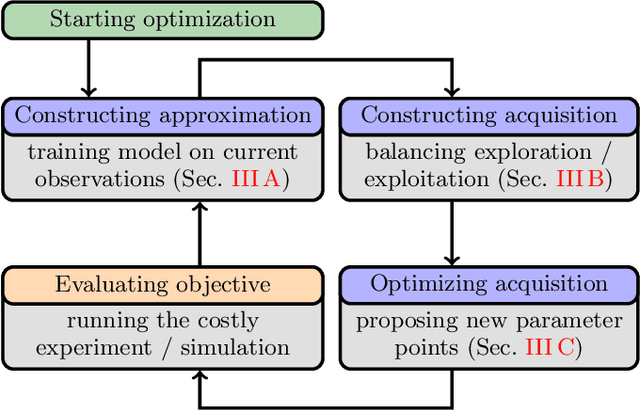


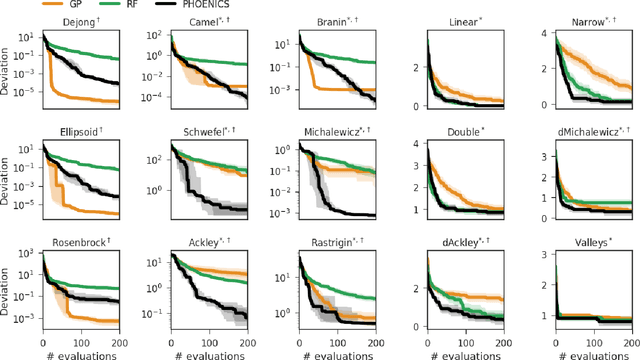
In this work we introduce PHOENICS, a probabilistic global optimization algorithm combining ideas from Bayesian optimization with concepts from Bayesian kernel density estimation. We propose an inexpensive acquisition function balancing the explorative and exploitative behavior of the algorithm. This acquisition function enables intuitive sampling strategies for an efficient parallel search of global minima. The performance of PHOENICS is assessed via an exhaustive benchmark study on a set of 15 discrete, quasi-discrete and continuous multidimensional functions. Unlike optimization methods based on Gaussian processes (GP) and random forests (RF), we show that PHOENICS is less sensitive to the nature of the co-domain, and outperforms GP and RF optimizations. We illustrate the performance of PHOENICS on the Oregonator, a difficult case-study describing a complex chemical reaction network. We demonstrate that only PHOENICS was able to reproduce qualitatively and quantitatively the target dynamic behavior of this nonlinear reaction dynamics. We recommend PHOENICS for rapid optimization of scalar, possibly non-convex, black-box unknown objective functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge