Learning Differentiable Surrogate Losses for Structured Prediction

Structured prediction involves learning to predict complex structures rather than simple scalar values. The main challenge arises from the non-Euclidean nature of the output space, which generally requires relaxing the problem formulation. Surrogate methods build on kernel-induced losses or more generally, loss functions admitting an Implicit Loss Embedding, and convert the original problem into a regression task followed by a decoding step. However, designing effective losses for objects with complex structures presents significant challenges and often requires domain-specific expertise. In this work, we introduce a novel framework in which a structured loss function, parameterized by neural networks, is learned directly from output training data through Contrastive Learning, prior to addressing the supervised surrogate regression problem. As a result, the differentiable loss not only enables the learning of neural networks due to the finite dimension of the surrogate space but also allows for the prediction of new structures of the output data via a decoding strategy based on gradient descent. Numerical experiments on supervised graph prediction problems show that our approach achieves similar or even better performance than methods based on a pre-defined kernel.

Restyling Unsupervised Concept Based Interpretable Networks with Generative Models

Developing inherently interpretable models for prediction has gained prominence in recent years. A subclass of these models, wherein the interpretable network relies on learning high-level concepts, are valued because of closeness of concept representations to human communication. However, the visualization and understanding of the learnt unsupervised dictionary of concepts encounters major limitations, specially for large-scale images. We propose here a novel method that relies on mapping the concept features to the latent space of a pretrained generative model. The use of a generative model enables high quality visualization, and naturally lays out an intuitive and interactive procedure for better interpretation of the learnt concepts. Furthermore, leveraging pretrained generative models has the additional advantage of making the training of the system more efficient. We quantitatively ascertain the efficacy of our method in terms of accuracy of the interpretable prediction network, fidelity of reconstruction, as well as faithfulness and consistency of learnt concepts. The experiments are conducted on multiple image recognition benchmarks for large-scale images. Project page available at https://jayneelparekh.github.io/VisCoIN_project_page/

Deep Sketched Output Kernel Regression for Structured Prediction

By leveraging the kernel trick in the output space, kernel-induced losses provide a principled way to define structured output prediction tasks for a wide variety of output modalities. In particular, they have been successfully used in the context of surrogate non-parametric regression, where the kernel trick is typically exploited in the input space as well. However, when inputs are images or texts, more expressive models such as deep neural networks seem more suited than non-parametric methods. In this work, we tackle the question of how to train neural networks to solve structured output prediction tasks, while still benefiting from the versatility and relevance of kernel-induced losses. We design a novel family of deep neural architectures, whose last layer predicts in a data-dependent finite-dimensional subspace of the infinite-dimensional output feature space deriving from the kernel-induced loss. This subspace is chosen as the span of the eigenfunctions of a randomly-approximated version of the empirical kernel covariance operator. Interestingly, this approach unlocks the use of gradient descent algorithms (and consequently of any neural architecture) for structured prediction. Experiments on synthetic tasks as well as real-world supervised graph prediction problems show the relevance of our method.

End-to-end Supervised Prediction of Arbitrary-size Graphs with Partially-Masked Fused Gromov-Wasserstein Matching

We present a novel end-to-end deep learning-based approach for Supervised Graph Prediction (SGP). We introduce an original Optimal Transport (OT)-based loss, the Partially-Masked Fused Gromov-Wasserstein loss (PM-FGW), that allows to directly leverage graph representations such as adjacency and feature matrices. PM-FGW exhibits all the desirable properties for SGP: it is node permutation invariant, sub-differentiable and handles graphs of different sizes by comparing their padded representations as well as their masking vectors. Moreover, we present a flexible transformer-based architecture that easily adapts to different types of input data. In the experimental section, three different tasks, a novel and challenging synthetic dataset (image2graph) and two real-world tasks, image2map and fingerprint2molecule - showcase the efficiency and versatility of the approach compared to competitors.

Anomaly component analysis

At the crossway of machine learning and data analysis, anomaly detection aims at identifying observations that exhibit abnormal behaviour. Be it measurement errors, disease development, severe weather, production quality default(s) (items) or failed equipment, financial frauds or crisis events, their on-time identification and isolation constitute an important task in almost any area of industry and science. While a substantial body of literature is devoted to detection of anomalies, little attention is payed to their explanation. This is the case mostly due to intrinsically non-supervised nature of the task and non-robustness of the exploratory methods like principal component analysis (PCA). We introduce a new statistical tool dedicated for exploratory analysis of abnormal observations using data depth as a score. Anomaly component analysis (shortly ACA) is a method that searches a low-dimensional data representation that best visualises and explains anomalies. This low-dimensional representation not only allows to distinguish groups of anomalies better than the methods of the state of the art, but as well provides a -- linear in variables and thus easily interpretable -- explanation for anomalies. In a comparative simulation and real-data study, ACA also proves advantageous for anomaly analysis with respect to methods present in the literature.

Fast kernel half-space depth for data with non-convex supports

Data depth is a statistical function that generalizes order and quantiles to the multivariate setting and beyond, with applications spanning over descriptive and visual statistics, anomaly detection, testing, etc. The celebrated halfspace depth exploits data geometry via an optimization program to deliver properties of invariances, robustness, and non-parametricity. Nevertheless, it implicitly assumes convex data supports and requires exponential computational cost. To tackle distribution's multimodality, we extend the halfspace depth in a Reproducing Kernel Hilbert Space (RKHS). We show that the obtained depth is intuitive and establish its consistency with provable concentration bounds that allow for homogeneity testing. The proposed depth can be computed using manifold gradient making faster than halfspace depth by several orders of magnitude. The performance of our depth is demonstrated through numerical simulations as well as applications such as anomaly detection on real data and homogeneity testing.

Tailoring Mixup to Data using Kernel Warping functions

Data augmentation is an essential building block for learning efficient deep learning models. Among all augmentation techniques proposed so far, linear interpolation of training data points, also called mixup, has found to be effective for a large panel of applications. While the majority of works have focused on selecting the right points to mix, or applying complex non-linear interpolation, we are interested in mixing similar points more frequently and strongly than less similar ones. To this end, we propose to dynamically change the underlying distribution of interpolation coefficients through warping functions, depending on the similarity between data points to combine. We define an efficient and flexible framework to do so without losing in diversity. We provide extensive experiments for classification and regression tasks, showing that our proposed method improves both performance and calibration of models. Code available in https://github.com/ENSTA-U2IS/torch-uncertainty

Exploiting Edge Features in Graphs with Fused Network Gromov-Wasserstein Distance

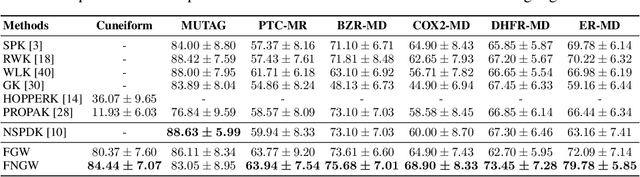
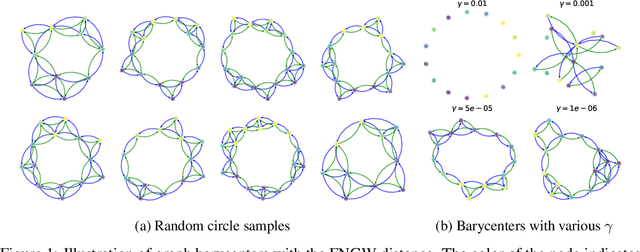
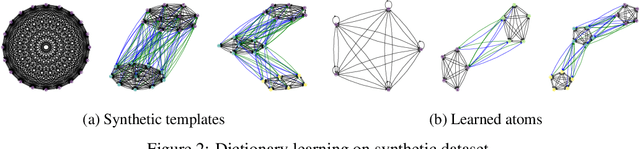
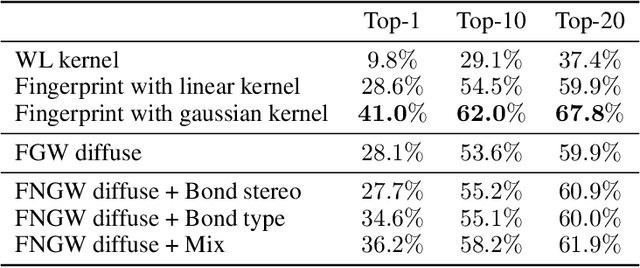
Pairwise comparison of graphs is key to many applications in Machine learning ranging from clustering, kernel-based classification/regression and more recently supervised graph prediction. Distances between graphs usually rely on informative representations of these structured objects such as bag of substructures or other graph embeddings. A recently popular solution consists in representing graphs as metric measure spaces, allowing to successfully leverage Optimal Transport, which provides meaningful distances allowing to compare them: the Gromov-Wasserstein distances. However, this family of distances overlooks edge attributes, which are essential for many structured objects. In this work, we introduce an extension of Gromov-Wasserstein distance for comparing graphs whose both nodes and edges have features. We propose novel algorithms for distance and barycenter computation. We empirically show the effectiveness of the novel distance in learning tasks where graphs occur in either input space or output space, such as classification and graph prediction.

Tackling Interpretability in Audio Classification Networks with Non-negative Matrix Factorization

This paper tackles two major problem settings for interpretability of audio processing networks, post-hoc and by-design interpretation. For post-hoc interpretation, we aim to interpret decisions of a network in terms of high-level audio objects that are also listenable for the end-user. This is extended to present an inherently interpretable model with high performance. To this end, we propose a novel interpreter design that incorporates non-negative matrix factorization (NMF). In particular, an interpreter is trained to generate a regularized intermediate embedding from hidden layers of a target network, learnt as time-activations of a pre-learnt NMF dictionary. Our methodology allows us to generate intuitive audio-based interpretations that explicitly enhance parts of the input signal most relevant for a network's decision. We demonstrate our method's applicability on a variety of classification tasks, including multi-label data for real-world audio and music.

Sketch In, Sketch Out: Accelerating both Learning and Inference for Structured Prediction with Kernels

Surrogate kernel-based methods offer a flexible solution to structured output prediction by leveraging the kernel trick in both input and output spaces. In contrast to energy-based models, they avoid to pay the cost of inference during training, while enjoying statistical guarantees. However, without approximation, these approaches are condemned to be used only on a limited amount of training data. In this paper, we propose to equip surrogate kernel methods with approximations based on sketching, seen as low rank projections of feature maps both on input and output feature maps. We showcase the approach on Input Output Kernel ridge Regression (or Kernel Dependency Estimation) and provide excess risk bounds that can be in turn directly plugged on the final predictive model. An analysis of the complexity in time and memory show that sketching the input kernel mostly reduces training time while sketching the output kernel allows to reduce the inference time. Furthermore, we show that Gaussian and sub-Gaussian sketches are admissible sketches in the sense that they induce projection operators ensuring a small excess risk. Experiments on different tasks consolidate our findings.