Fast kernel half-space depth for data with non-convex supports

Data depth is a statistical function that generalizes order and quantiles to the multivariate setting and beyond, with applications spanning over descriptive and visual statistics, anomaly detection, testing, etc. The celebrated halfspace depth exploits data geometry via an optimization program to deliver properties of invariances, robustness, and non-parametricity. Nevertheless, it implicitly assumes convex data supports and requires exponential computational cost. To tackle distribution's multimodality, we extend the halfspace depth in a Reproducing Kernel Hilbert Space (RKHS). We show that the obtained depth is intuitive and establish its consistency with provable concentration bounds that allow for homogeneity testing. The proposed depth can be computed using manifold gradient making faster than halfspace depth by several orders of magnitude. The performance of our depth is demonstrated through numerical simulations as well as applications such as anomaly detection on real data and homogeneity testing.

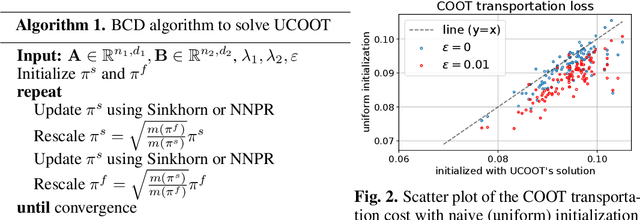
Unbalanced CO-Optimal Transport

Optimal transport (OT) compares probability distributions by computing a meaningful alignment between their samples. CO-optimal transport (COOT) takes this comparison further by inferring an alignment between features as well. While this approach leads to better alignments and generalizes both OT and Gromov-Wasserstein distances, we provide a theoretical result showing that it is sensitive to outliers that are omnipresent in real-world data. This prompts us to propose unbalanced COOT for which we provably show its robustness to noise in the compared datasets. To the best of our knowledge, this is the first such result for OT methods in incomparable spaces. With this result in hand, we provide empirical evidence of this robustness for the challenging tasks of heterogeneous domain adaptation with and without varying proportions of classes and simultaneous alignment of samples and features across single-cell measurements.

Averaging Spatio-temporal Signals using Optimal Transport and Soft Alignments

Several fields in science, from genomics to neuroimaging, require monitoring populations (measures) that evolve with time. These complex datasets, describing dynamics with both time and spatial components, pose new challenges for data analysis. We propose in this work a new framework to carry out averaging of these datasets, with the goal of synthesizing a representative template trajectory from multiple trajectories. We show that this requires addressing three sources of invariance: shifts in time, space, and total population size (or mass/amplitude). Here we draw inspiration from dynamic time warping (DTW), optimal transport (OT) theory and its unbalanced extension (UOT) to propose a criterion that can address all three issues. This proposal leverages a smooth formulation of DTW (Soft-DTW) that is shown to capture temporal shifts, and UOT to handle both variations in space and size. Our proposed loss can be used to define spatio-temporal barycenters as Fr\'echet means. Using Fenchel duality, we show how these barycenters can be computed efficiently, in parallel, via a novel variant of entropy-regularized debiased UOT. Experiments on handwritten letters and brain imaging data confirm our theoretical findings and illustrate the effectiveness of the proposed loss for spatio-temporal data.

Factored couplings in multi-marginal optimal transport via difference of convex programming

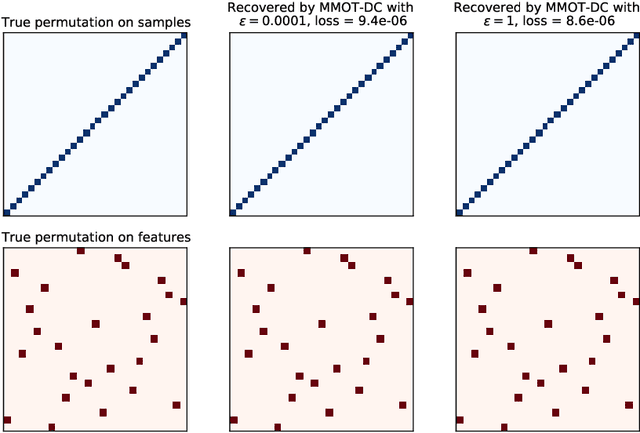
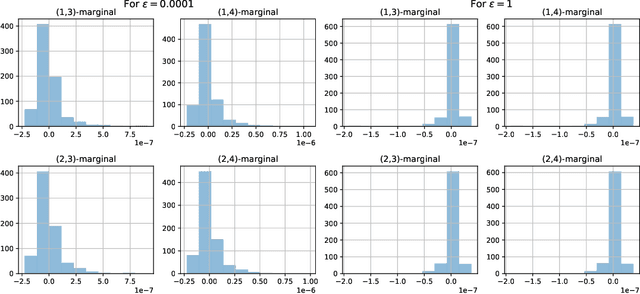
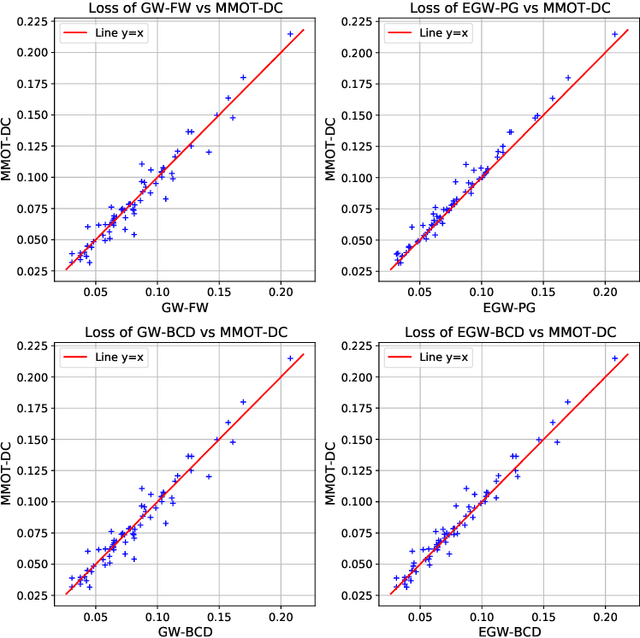
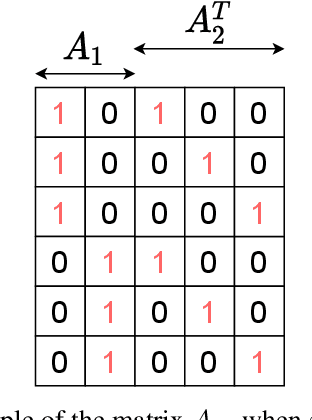
Optimal transport (OT) theory underlies many emerging machine learning (ML) methods nowadays solving a wide range of tasks such as generative modeling, transfer learning and information retrieval. These latter works, however, usually build upon a traditional OT setup with two distributions, while leaving a more general multi-marginal OT formulation somewhat unexplored. In this paper, we study the multi-marginal OT (MMOT) problem and unify several popular OT methods under its umbrella by promoting structural information on the coupling. We show that incorporating such structural information into MMOT results in an instance of a different of convex (DC) programming problem allowing us to solve it numerically. Despite high computational cost of the latter procedure, the solutions provided by DC optimization are usually as qualitative as those obtained using currently employed optimization schemes.

Debiased Sinkhorn barycenters

Entropy regularization in optimal transport (OT) has been the driver of many recent interests for Wasserstein metrics and barycenters in machine learning. It allows to keep the appealing geometrical properties of the unregularized Wasserstein distance while having a significantly lower complexity thanks to Sinkhorn's algorithm. However, entropy brings some inherent smoothing bias, resulting for example in blurred barycenters. This side effect has prompted an increasing temptation in the community to settle for a slower algorithm such as log-domain stabilized Sinkhorn which breaks the parallel structure that can be leveraged on GPUs, or even go back to unregularized OT. Here we show how this bias is tightly linked to the reference measure that defines the entropy regularizer and propose debiased Wasserstein barycenters that preserve the best of both worlds: fast Sinkhorn-like iterations without entropy smoothing. Theoretically, we prove that the entropic OT barycenter of univariate Gaussians is a Gaussian and quantify its variance bias. This result is obtained by extending the differentiability and convexity of entropic OT to sub-Gaussian measures with unbounded supports. Empirically, we illustrate the reduced blurring and the computational advantage on various applications.

Spatio-Temporal Alignments: Optimal transport through space and time

Comparing data defined over space and time is notoriously hard, because it involves quantifying both spatial and temporal variability, while at the same time taking into account the chronological structure of data. Dynamic Time Warping (DTW) computes an optimal alignment between time series in agreement with the chronological order, but is inherently blind to spatial shifts. In this paper, we propose Spatio-Temporal Alignments (STA), a new differentiable formulation of DTW, in which spatial differences between time samples are accounted for using regularized optimal transport (OT). Our temporal alignments are handled through a smooth variant of DTW called soft-DTW, for which we prove a new property: soft-DTW increases quadratically with time shifts. The cost matrix within soft-DTW that we use are computed using unbalanced OT, to handle the case in which observations are not normalized probabilities. Experiments on handwritten letters and brain imaging data confirm our theoretical findings and illustrate the effectiveness of STA as a dissimilarity for spatio-temporal data.

Multi-subject MEG/EEG source imaging with sparse multi-task regression

Magnetoencephalography and electroencephalography (M/EEG) are non-invasive modalities that measure the weak electromagnetic fields generated by neural activity. Estimating the location and magnitude of the current sources that generated these electromagnetic fields is a challenging ill-posed regression problem known as \emph{source imaging}. When considering a group study, a common approach consists in carrying out the regression tasks independently for each subject. An alternative is to jointly localize sources for all subjects taken together, while enforcing some similarity between them. By pooling all measurements in a single multi-task regression, one makes the problem better posed, offering the ability to identify more sources and with greater precision. The Minimum Wasserstein Estimates (MWE) promotes focal activations that do not perfectly overlap for all subjects, thanks to a regularizer based on Optimal Transport (OT) metrics. MWE promotes spatial proximity on the cortical mantel while coping with the varying noise levels across subjects. On realistic simulations, MWE decreases the localization error by up to 4 mm per source compared to individual solutions. Experiments on the Cam-CAN dataset show a considerable improvement in spatial specificity in population imaging. Our analysis of a multimodal dataset shows how multi-subject source localization closes the gap between MEG and fMRI for brain mapping.

Group level MEG/EEG source imaging via optimal transport: minimum Wasserstein estimates

Magnetoencephalography (MEG) and electroencephalogra-phy (EEG) are non-invasive modalities that measure the weak electromagnetic fields generated by neural activity. Inferring the location of the current sources that generated these magnetic fields is an ill-posed inverse problem known as source imaging. When considering a group study, a baseline approach consists in carrying out the estimation of these sources independently for each subject. The ill-posedness of each problem is typically addressed using sparsity promoting regularizations. A straightforward way to define a common pattern for these sources is then to average them. A more advanced alternative relies on a joint localization of sources for all subjects taken together, by enforcing some similarity across all estimated sources. An important advantage of this approach is that it consists in a single estimation in which all measurements are pooled together, making the inverse problem better posed. Such a joint estimation poses however a few challenges, notably the selection of a valid regularizer that can quantify such spatial similarities. We propose in this work a new procedure that can do so while taking into account the geometrical structure of the cortex. We call this procedure Minimum Wasserstein Estimates (MWE). The benefits of this model are twofold. First, joint inference allows to pool together the data of different brain geometries, accumulating more spatial information. Second, MWE are defined through Optimal Transport (OT) metrics which provide a tool to model spatial proximity between cortical sources of different subjects, hence not enforcing identical source location in the group. These benefits allow MWE to be more accurate than standard MEG source localization techniques. To support these claims, we perform source localization on realistic MEG simulations based on forward operators derived from MRI scans. On a visual task dataset, we demonstrate how MWE infer neural patterns similar to functional Magnetic Resonance Imaging (fMRI) maps.

Wasserstein regularization for sparse multi-task regression

Two important elements have driven recent innovation in the field of regression: sparsity-inducing regularization, to cope with high-dimensional problems; multi-task learning through joint parameter estimation, to augment the number of training samples. Both approaches complement each other in the sense that a joint estimation results in more samples, which are needed to estimate sparse models accurately, whereas sparsity promotes models that act on subsets of related variables. This idea has driven the proposal of block regularizers such as L1/Lq norms, which however effective, require that active regressors strictly overlap. In this paper, we propose a more flexible convex regularizer based on unbalanced optimal transport (OT) theory. That regularizer promotes parameters that are close, according to the OT geometry, which takes into account a prior geometric knowledge on the regressor variables. We derive an efficient algorithm based on a regularized formulation of optimal transport, which iterates through applications of Sinkhorn's algorithm along with coordinate descent iterations. The performance of our model is demonstrated on regular grids and complex triangulated geometries of the cortex with an application in neuroimaging.