Revisiting invariances and introducing priors in Gromov-Wasserstein distances

Gromov-Wasserstein distance has found many applications in machine learning due to its ability to compare measures across metric spaces and its invariance to isometric transformations. However, in certain applications, this invariance property can be too flexible, thus undesirable. Moreover, the Gromov-Wasserstein distance solely considers pairwise sample similarities in input datasets, disregarding the raw feature representations. We propose a new optimal transport-based distance, called Augmented Gromov-Wasserstein, that allows for some control over the level of rigidity to transformations. It also incorporates feature alignments, enabling us to better leverage prior knowledge on the input data for improved performance. We present theoretical insights into the proposed metric. We then demonstrate its usefulness for single-cell multi-omic alignment tasks and a transfer learning scenario in machine learning.

Analysis and Comparison of Two-Level KFAC Methods for Training Deep Neural Networks

As a second-order method, the Natural Gradient Descent (NGD) has the ability to accelerate training of neural networks. However, due to the prohibitive computational and memory costs of computing and inverting the Fisher Information Matrix (FIM), efficient approximations are necessary to make NGD scalable to Deep Neural Networks (DNNs). Many such approximations have been attempted. The most sophisticated of these is KFAC, which approximates the FIM as a block-diagonal matrix, where each block corresponds to a layer of the neural network. By doing so, KFAC ignores the interactions between different layers. In this work, we investigate the interest of restoring some low-frequency interactions between the layers by means of two-level methods. Inspired from domain decomposition, several two-level corrections to KFAC using different coarse spaces are proposed and assessed. The obtained results show that incorporating the layer interactions in this fashion does not really improve the performance of KFAC. This suggests that it is safe to discard the off-diagonal blocks of the FIM, since the block-diagonal approach is sufficiently robust, accurate and economical in computation time.

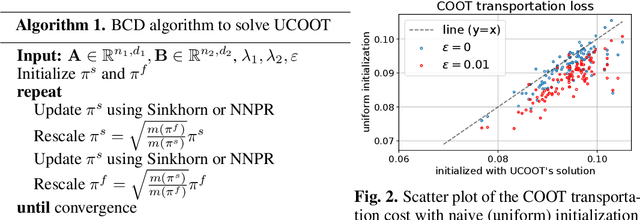
Unbalanced CO-Optimal Transport

Optimal transport (OT) compares probability distributions by computing a meaningful alignment between their samples. CO-optimal transport (COOT) takes this comparison further by inferring an alignment between features as well. While this approach leads to better alignments and generalizes both OT and Gromov-Wasserstein distances, we provide a theoretical result showing that it is sensitive to outliers that are omnipresent in real-world data. This prompts us to propose unbalanced COOT for which we provably show its robustness to noise in the compared datasets. To the best of our knowledge, this is the first such result for OT methods in incomparable spaces. With this result in hand, we provide empirical evidence of this robustness for the challenging tasks of heterogeneous domain adaptation with and without varying proportions of classes and simultaneous alignment of samples and features across single-cell measurements.

Efficient Approximations of the Fisher Matrix in Neural Networks using Kronecker Product Singular Value Decomposition

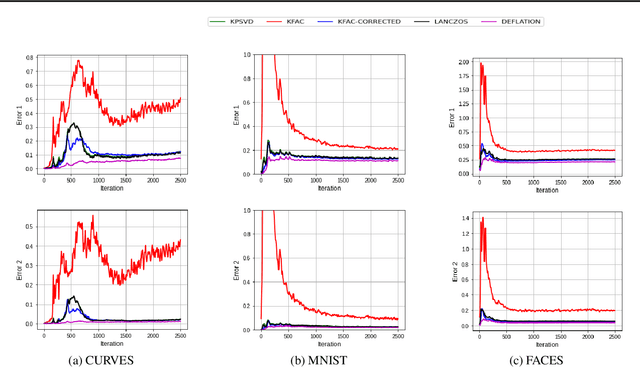
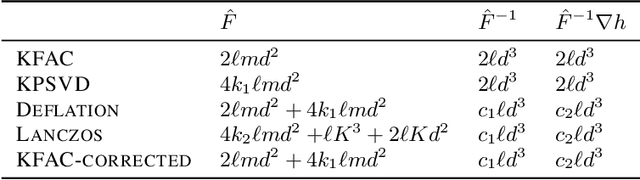
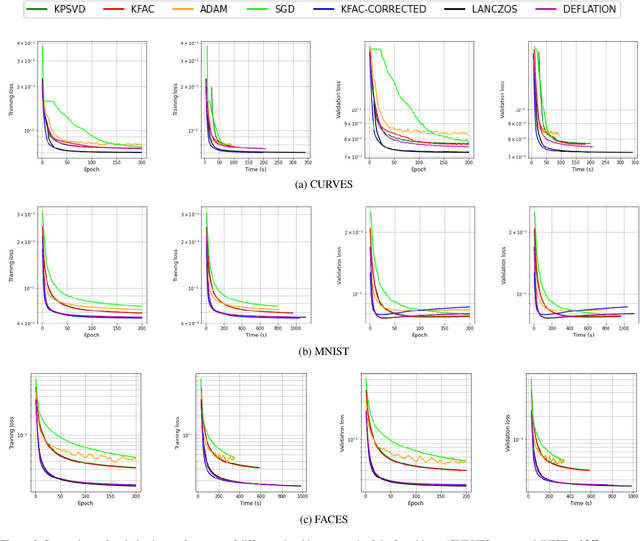
Several studies have shown the ability of natural gradient descent to minimize the objective function more efficiently than ordinary gradient descent based methods. However, the bottleneck of this approach for training deep neural networks lies in the prohibitive cost of solving a large dense linear system corresponding to the Fisher Information Matrix (FIM) at each iteration. This has motivated various approximations of either the exact FIM or the empirical one. The most sophisticated of these is KFAC, which involves a Kronecker-factored block diagonal approximation of the FIM. With only a slight additional cost, a few improvements of KFAC from the standpoint of accuracy are proposed. The common feature of the four novel methods is that they rely on a direct minimization problem, the solution of which can be computed via the Kronecker product singular value decomposition technique. Experimental results on the three standard deep auto-encoder benchmarks showed that they provide more accurate approximations to the FIM. Furthermore, they outperform KFAC and state-of-the-art first-order methods in terms of optimization speed.

Factored couplings in multi-marginal optimal transport via difference of convex programming

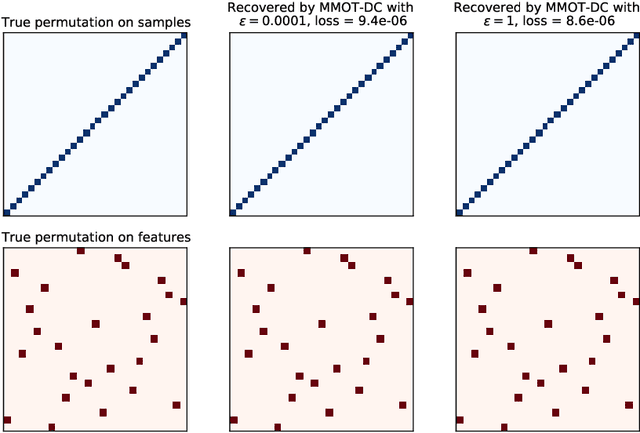
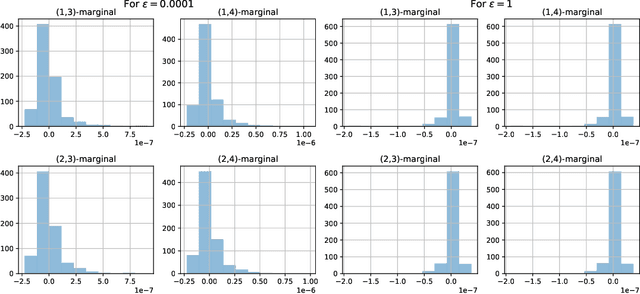
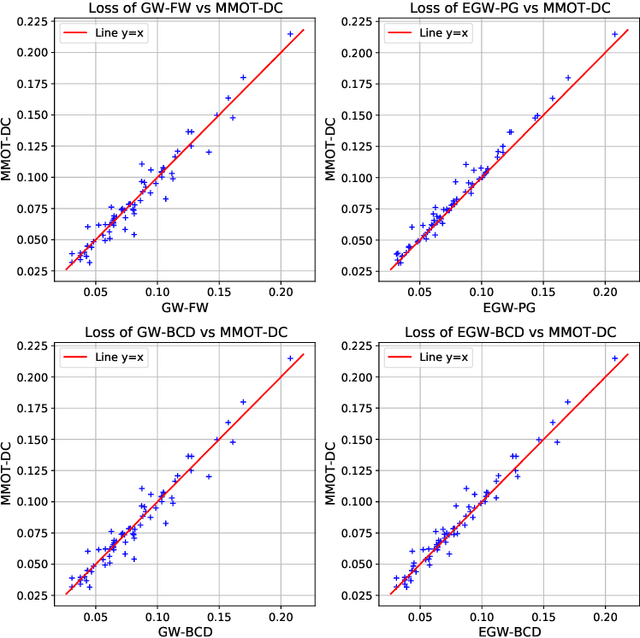
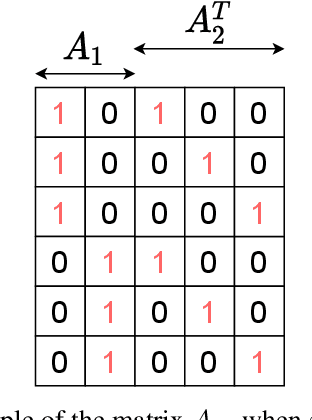
Optimal transport (OT) theory underlies many emerging machine learning (ML) methods nowadays solving a wide range of tasks such as generative modeling, transfer learning and information retrieval. These latter works, however, usually build upon a traditional OT setup with two distributions, while leaving a more general multi-marginal OT formulation somewhat unexplored. In this paper, we study the multi-marginal OT (MMOT) problem and unify several popular OT methods under its umbrella by promoting structural information on the coupling. We show that incorporating such structural information into MMOT results in an instance of a different of convex (DC) programming problem allowing us to solve it numerically. Despite high computational cost of the latter procedure, the solutions provided by DC optimization are usually as qualitative as those obtained using currently employed optimization schemes.