Learning Quantization in LDPC Decoders

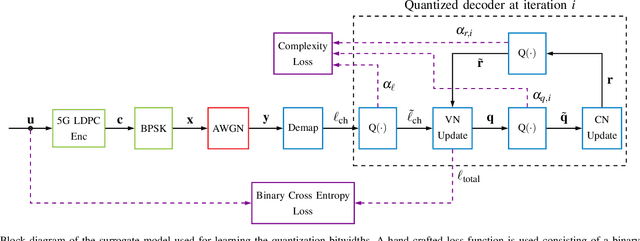
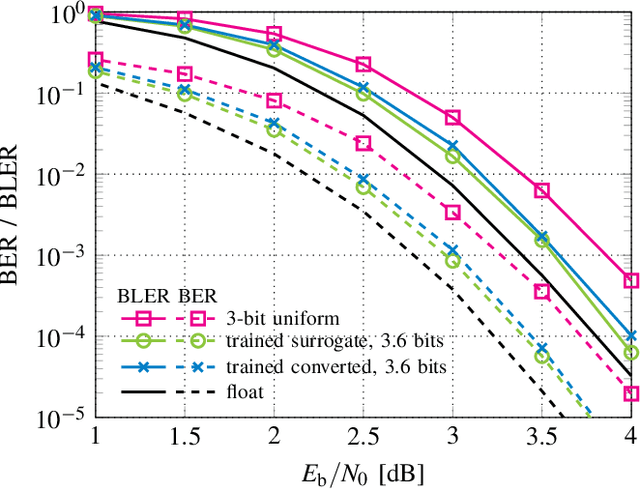
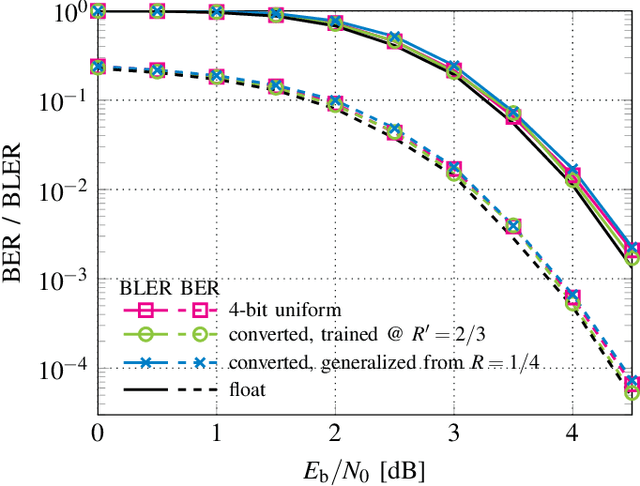
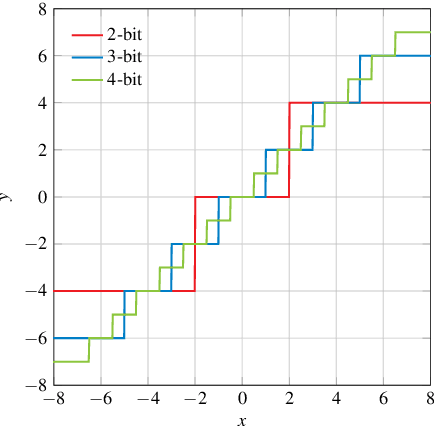
Finding optimal message quantization is a key requirement for low complexity belief propagation (BP) decoding. To this end, we propose a floating-point surrogate model that imitates quantization effects as additions of uniform noise, whose amplitudes are trainable variables. We verify that the surrogate model closely matches the behavior of a fixed-point implementation and propose a hand-crafted loss function to realize a trade-off between complexity and error-rate performance. A deep learning-based method is then applied to optimize the message bitwidths. Moreover, we show that parameter sharing can both ensure implementation-friendly solutions and results in faster training convergence than independent parameters. We provide simulation results for 5G low-density parity-check (LDPC) codes and report an error-rate performance within 0.2 dB of floating-point decoding at an average message quantization bitwidth of 3.1 bits. In addition, we show that the learned bitwidths also generalize to other code rates and channels.

Vector spaces as Kripke frames

In recent years, the compositional distributional approach in computational linguistics has opened the way for an integration of the \emph{lexical} aspects of meaning into Lambek's type-logical grammar program. This approach is based on the observation that a sound semantics for the associative, commutative and unital Lambek calculus can be based on vector spaces by interpreting fusion as the tensor product of vector spaces. In this paper, we build on this observation and extend it to a `vector space semantics' for the {\em general} Lambek calculus, based on {\em algebras over a field} $\mathbb{K}$ (or $\mathbb{K}$-algebras), i.e. vector spaces endowed with a bilinear binary product. Such structures are well known in algebraic geometry and algebraic topology, since they are important instances of Lie algebras and Hopf algebras. Applying results and insights from duality and representation theory for the algebraic semantics of nonclassical logics, we regard $\mathbb{K}$-algebras as `Kripke frames' the complex algebras of which are complete residuated lattices. This perspective makes it possible to establish a systematic connection between vector space semantics and the standard Routley-Meyer semantics of (modal) substructural logics.

Towards Optimal Power Control via Ensembling Deep Neural Networks

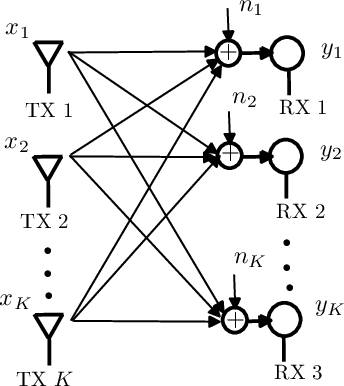
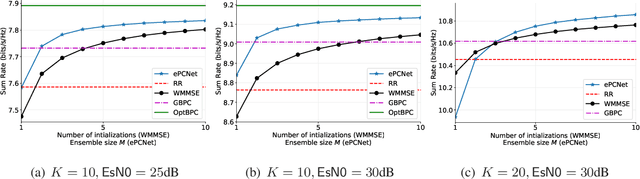
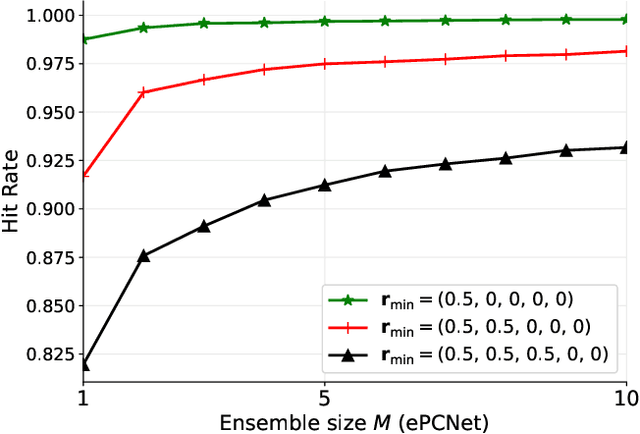
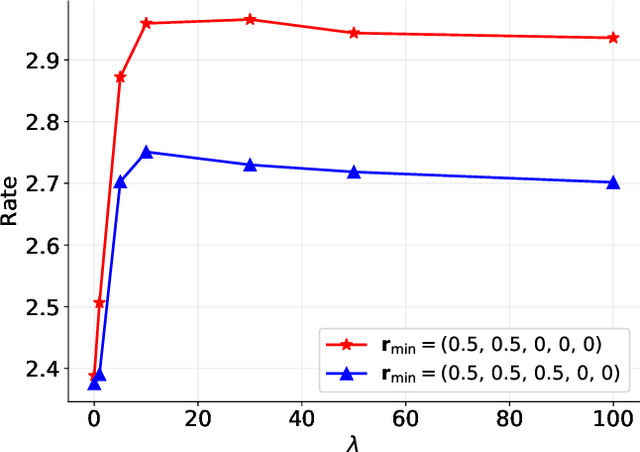
A deep neural network (DNN) based power control method is proposed, which aims at solving the non-convex optimization problem of maximizing the sum rate of a multi-user interference channel. Towards this end, we first present PCNet, which is a multi-layer fully connected neural network that is specifically designed for the power control problem. PCNet takes the channel coefficients as input and outputs the transmit power of all users. A key challenge in training a DNN for the power control problem is the lack of ground truth, i.e., the optimal power allocation is unknown. To address this issue, PCNet leverages the unsupervised learning strategy and directly maximizes the sum rate in the training phase. Observing that a single PCNet does not globally outperform the existing solutions, we further propose ePCNet, a network ensemble with multiple PCNets trained independently. Simulation results show that for the standard symmetric multi-user Gaussian interference channel, ePCNet can outperform all state-of-the-art power control methods by 1.2%-4.6% under a variety of system configurations. Furthermore, the performance improvement of ePCNet comes with a reduced computational complexity.

An Iterative BP-CNN Architecture for Channel Decoding

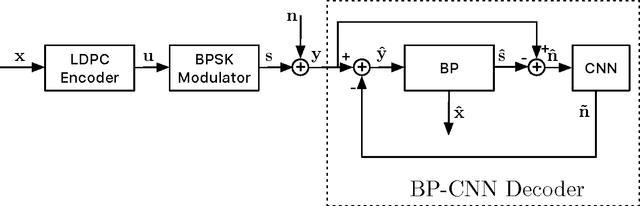
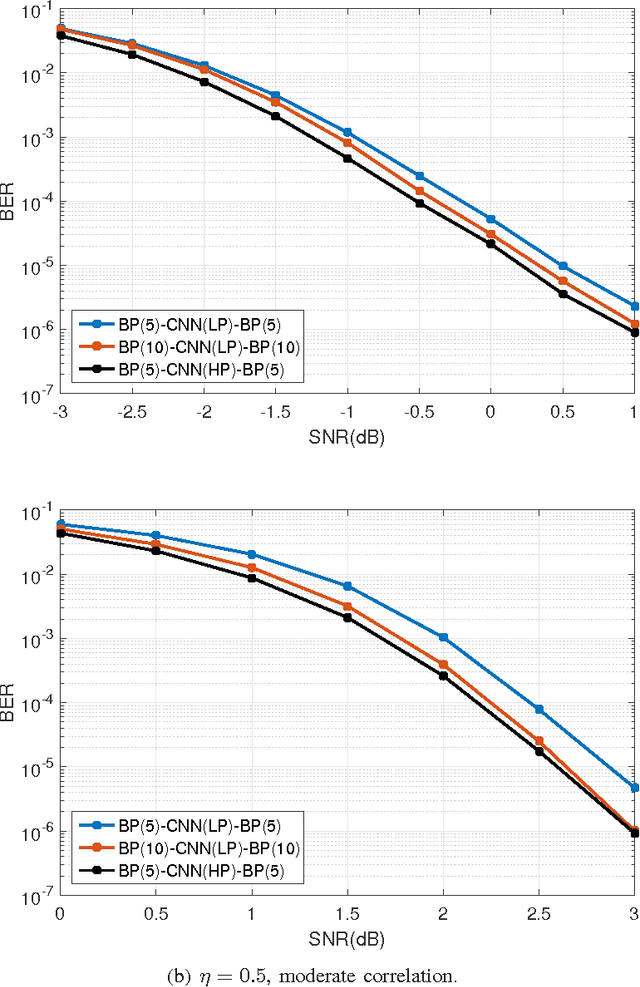
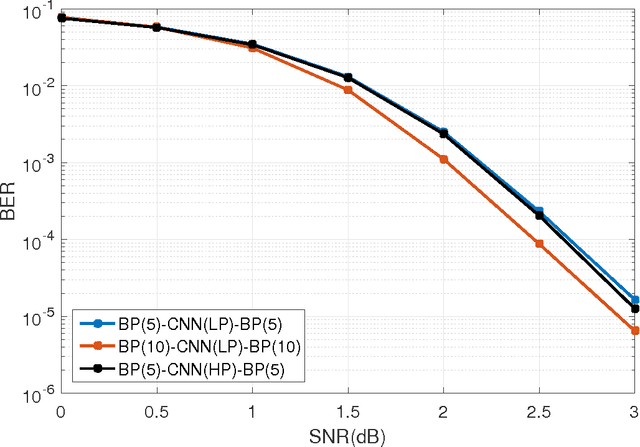
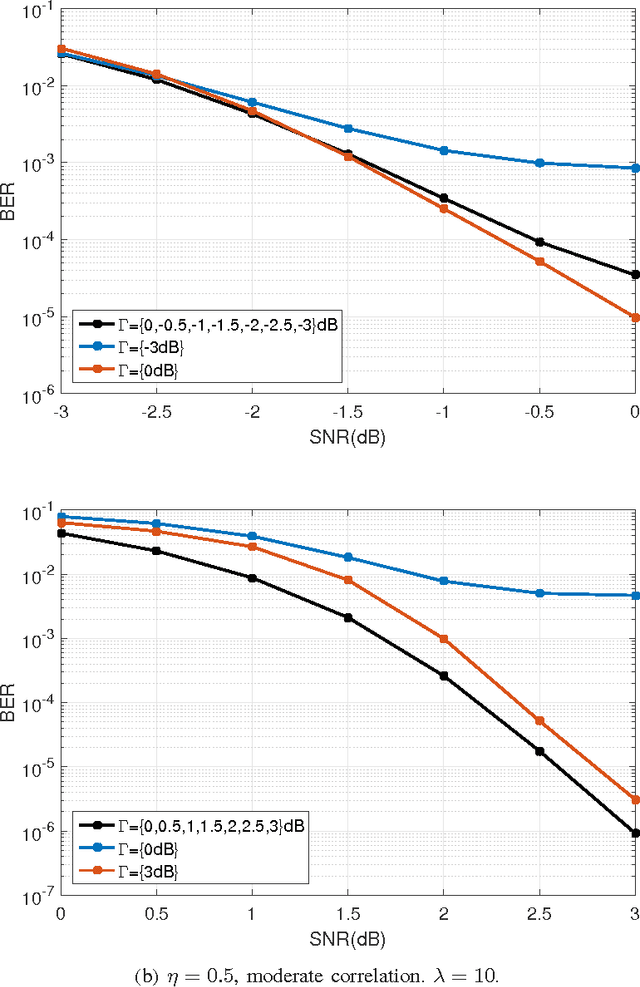
Inspired by recent advances in deep learning, we propose a novel iterative BP-CNN architecture for channel decoding under correlated noise. This architecture concatenates a trained convolutional neural network (CNN) with a standard belief-propagation (BP) decoder. The standard BP decoder is used to estimate the coded bits, followed by a CNN to remove the estimation errors of the BP decoder and obtain a more accurate estimation of the channel noise. Iterating between BP and CNN will gradually improve the decoding SNR and hence result in better decoding performance. To train a well-behaved CNN model, we define a new loss function which involves not only the accuracy of the noise estimation but also the normality test for the estimation errors, i.e., to measure how likely the estimation errors follow a Gaussian distribution. The introduction of the normality test to the CNN training shapes the residual noise distribution and further reduces the BER of the iterative decoding, compared to using the standard quadratic loss function. We carry out extensive experiments to analyze and verify the proposed framework. The iterative BP-CNN decoder has better BER performance with lower complexity, is suitable for parallel implementation, does not rely on any specific channel model or encoding method, and is robust against training mismatches. All of these features make it a good candidate for decoding modern channel codes.