Graph Search based Polar Code Design

It is well known that to fulfill their full potential, the design of polar codes must be tailored to their intended decoding algorithm. While for successive cancellation (SC) decoding, information theoretically optimal constructions are available, the code design for other decoding algorithms (such as belief propagation (BP) decoding) can only be optimized using extensive Monte Carlo simulations. We propose to view the design process of polar codes as a graph search problem and thereby approaching it more systematically. Based on this formalism, the design-time complexity can be significantly reduced compared to state-of-the-art Genetic Algorithm (GenAlg) and deep learning-based design algorithms. Moreover, sequences of rate-compatible polar codes can be efficiently found. Finally, we analyze both the complexity of the proposed algorithm and the error-rate performance of the constructed codes.

Learning Quantization in LDPC Decoders

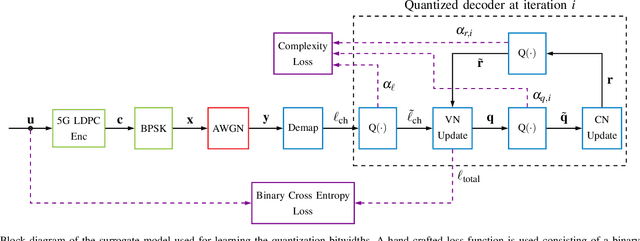
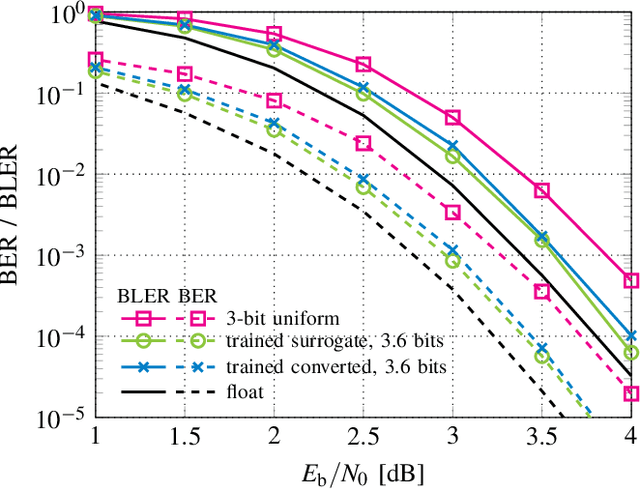
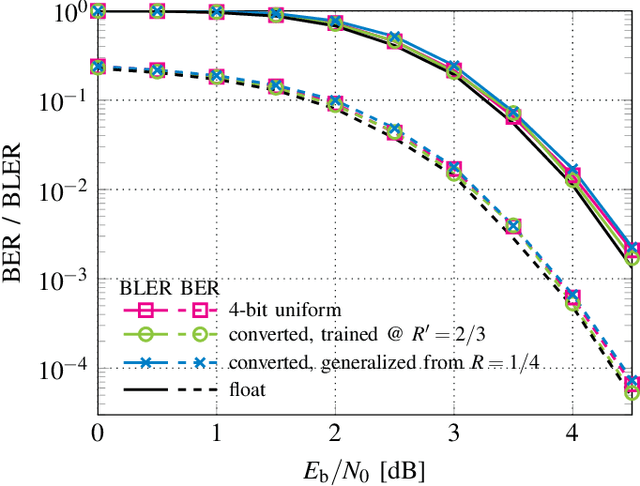
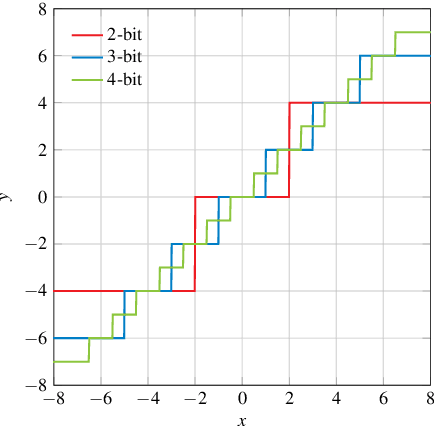
Finding optimal message quantization is a key requirement for low complexity belief propagation (BP) decoding. To this end, we propose a floating-point surrogate model that imitates quantization effects as additions of uniform noise, whose amplitudes are trainable variables. We verify that the surrogate model closely matches the behavior of a fixed-point implementation and propose a hand-crafted loss function to realize a trade-off between complexity and error-rate performance. A deep learning-based method is then applied to optimize the message bitwidths. Moreover, we show that parameter sharing can both ensure implementation-friendly solutions and results in faster training convergence than independent parameters. We provide simulation results for 5G low-density parity-check (LDPC) codes and report an error-rate performance within 0.2 dB of floating-point decoding at an average message quantization bitwidth of 3.1 bits. In addition, we show that the learned bitwidths also generalize to other code rates and channels.

Deep Learning-based Polar Code Design

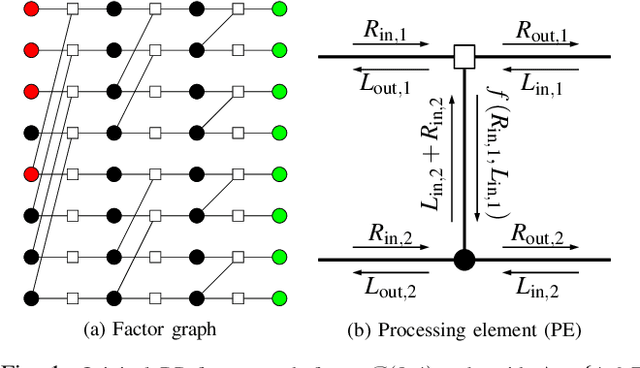
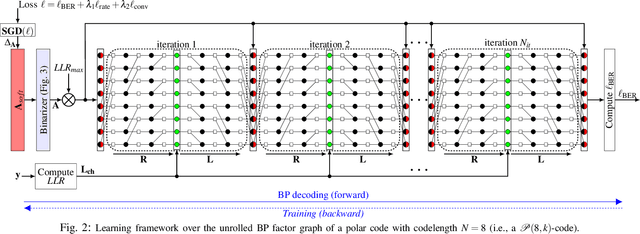
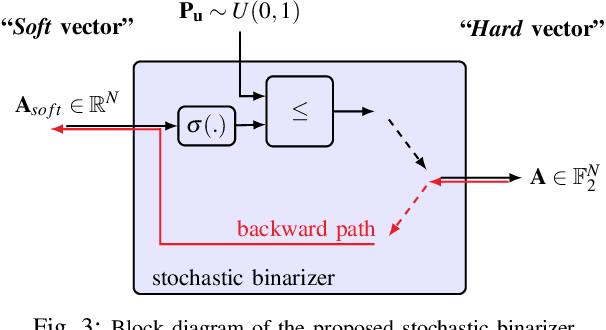
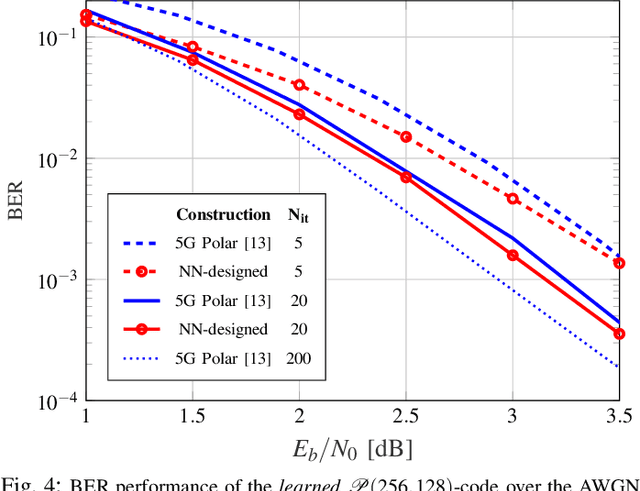
In this work, we introduce a deep learning-based polar code construction algorithm. The core idea is to represent the information/frozen bit indices of a polar code as a binary vector which can be interpreted as trainable weights of a neural network (NN). For this, we demonstrate how this binary vector can be relaxed to a soft-valued vector, facilitating the learning process through gradient descent and enabling an efficient code construction. We further show how different polar code design constraints (e.g., code rate) can be taken into account by means of careful binary-to-soft and soft-to-binary conversions, along with rate-adjustment after each learning iteration. Besides its conceptual simplicity, this approach benefits from having the "decoder-in-the-loop", i.e., the nature of the decoder is inherently taken into consideration while learning (designing) the polar code. We show results for belief propagation (BP) decoding over both AWGN and Rayleigh fading channels with considerable performance gains over state-of-the-art construction schemes.

Decoder-tailored Polar Code Design Using the Genetic Algorithm

We propose a new framework for constructing polar codes (i.e., selecting the frozen bit positions) for arbitrary channels, and tailored to a given decoding algorithm, rather than based on the (not necessarily optimal) assumption of successive cancellation (SC) decoding. The proposed framework is based on the Genetic Algorithm (GenAlg), where populations (i.e., collections) of information sets evolve successively via evolutionary transformations based on their individual error-rate performance. These populations converge towards an information set that fits both the decoding behavior and the defined channel. Using our proposed algorithm over the additive white Gaussian noise (AWGN) channel, we construct a polar code of length 2048 with code rate 0.5, without the CRC-aid, tailored to plain successive cancellation list (SCL) decoding, achieving the same error-rate performance as the CRC-aided SCL decoding, and leading to a coding gain of 1 dB at BER of $10^{-6}$. Further, a belief propagation (BP)-tailored construction approaches the SCL error-rate performance without any modifications in the decoding algorithm itself. The performance gains can be attributed to the significant reduction in the total number of low-weight codewords. To demonstrate the flexibility, coding gains for the Rayleigh channel are shown under SCL and BP decoding. Besides improvements in error-rate performance, we show that, when required, the GenAlg can be also set up to reduce the decoding complexity, e.g., the SCL list size or the number of BP iterations can be reduced, while maintaining the same error-rate performance.

Genetic Algorithm-based Polar Code Construction for the AWGN Channel

We propose a new polar code construction framework (i.e., selecting the frozen bit positions) for the additive white Gaussian noise (AWGN) channel, tailored to a given decoding algorithm, rather than based on the (not necessarily optimal) assumption of successive cancellation (SC) decoding. The proposed framework is based on the Genetic Algorithm (GenAlg), where populations (i.e., collections) of information sets evolve successively via evolutionary transformations based on their individual error-rate performance. These populations converge towards an information set that fits the decoding behavior. Using our proposed algorithm, we construct a polar code of length 2048 with code rate 0.5, without the CRC-aid, tailored to plain successive cancellation list (SCL) decoding, achieving the same error-rate performance as the CRC-aided SCL decoding, and leading to a coding gain of 1 dB at BER of $10^{-6}$. Further, a belief propagation (BP)-tailored polar code approaches the SCL error-rate performance without any modifications in the decoding algorithm itself.