Deep Learning-based Polar Code Design
Paper and Code
Sep 27, 2019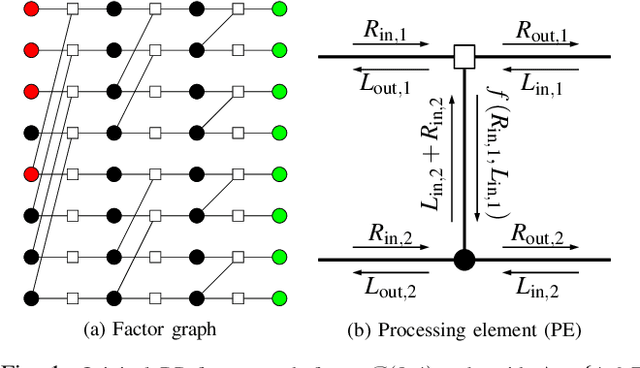
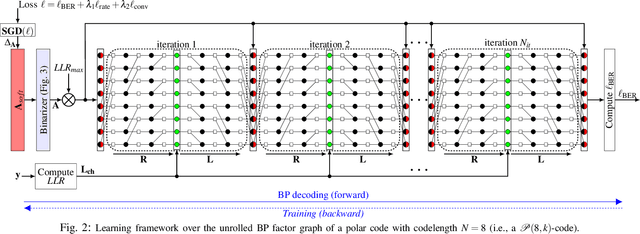
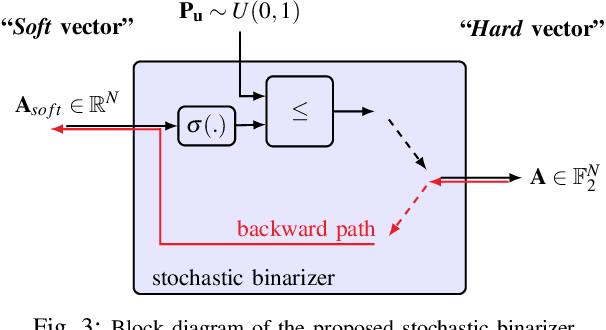
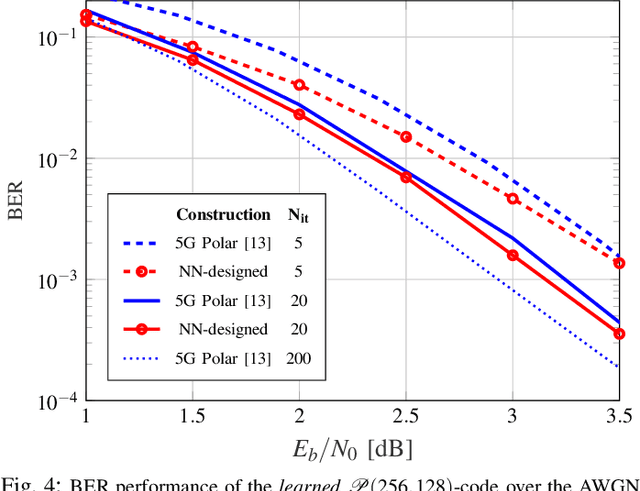
In this work, we introduce a deep learning-based polar code construction algorithm. The core idea is to represent the information/frozen bit indices of a polar code as a binary vector which can be interpreted as trainable weights of a neural network (NN). For this, we demonstrate how this binary vector can be relaxed to a soft-valued vector, facilitating the learning process through gradient descent and enabling an efficient code construction. We further show how different polar code design constraints (e.g., code rate) can be taken into account by means of careful binary-to-soft and soft-to-binary conversions, along with rate-adjustment after each learning iteration. Besides its conceptual simplicity, this approach benefits from having the "decoder-in-the-loop", i.e., the nature of the decoder is inherently taken into consideration while learning (designing) the polar code. We show results for belief propagation (BP) decoding over both AWGN and Rayleigh fading channels with considerable performance gains over state-of-the-art construction schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge