Bounds for Joint Detection and Decoding on the Binary-Input AWGN Channel

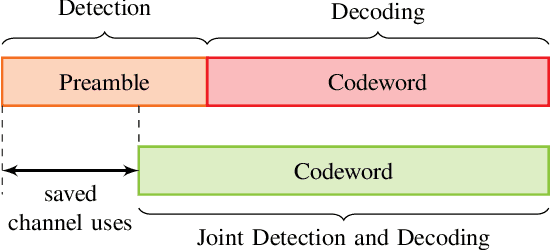
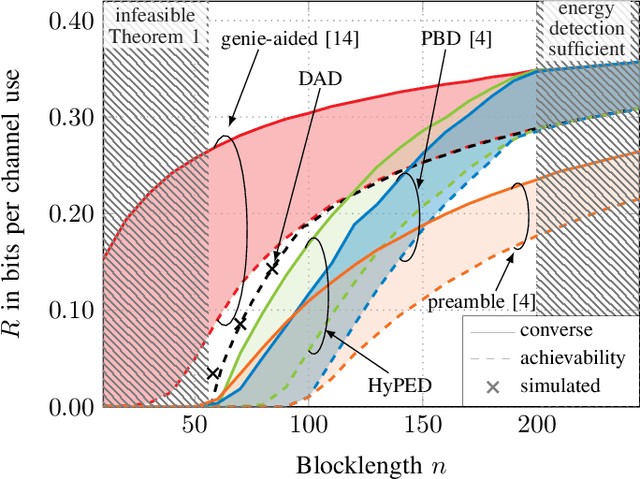
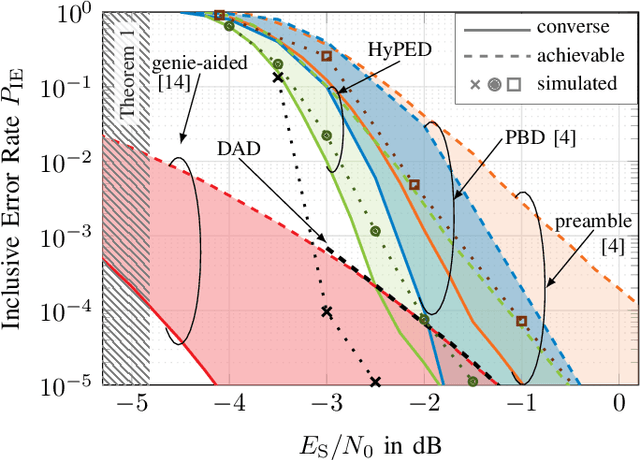
For asynchronous transmission of short blocks, preambles for packet detection contribute a non-negligible overhead. To reduce the required preamble length, joint detection and decoding (JDD) techniques have been proposed that additionally utilize the payload part of the packet for detection. In this paper, we analyze two instances of JDD, namely hybrid preamble and energy detection (HyPED) and decoder-aided detection (DAD). While HyPED combines the preamble with energy detection for the payload, DAD also uses the output of a channel decoder. For these systems, we propose novel achievability and converse bounds for the rates over the binary-input additive white Gaussian noise (BI-AWGN) channel. Moreover, we derive a general bound on the required blocklength for JDD. Both the theoretical bound and the simulation of practical codebooks show that the rate of DAD quickly approaches that of synchronous transmission.

Graph Neural Network-based Joint Equalization and Decoding

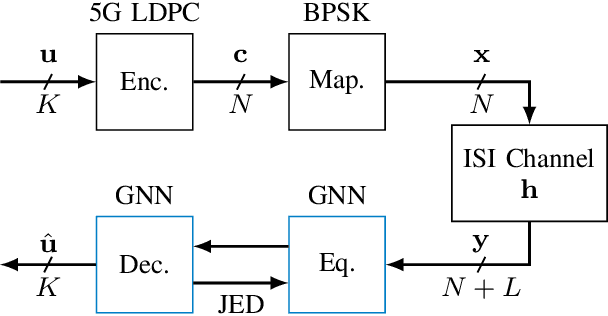
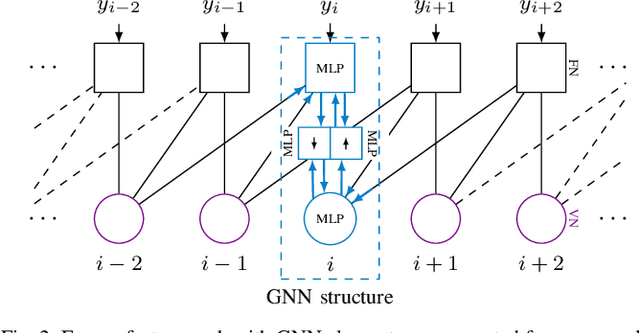
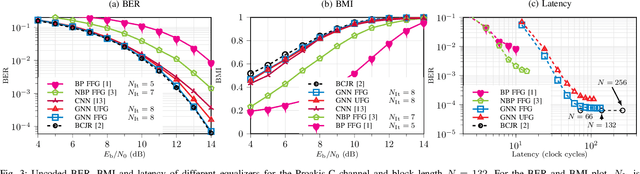
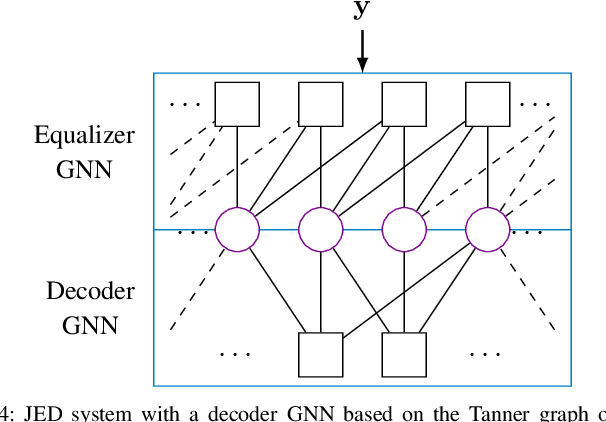
This paper proposes to use graph neural networks (GNNs) for equalization, that can also be used to perform joint equalization and decoding (JED). For equalization, the GNN is build upon the factor graph representations of the channel, while for JED, the factor graph is expanded by the Tanner graph of the parity-check matrix (PCM) of the channel code, sharing the variable nodes (VNs). A particularly advantageous property of the GNN is the robustness against cycles in the factor graphs which is the main problem for belief propagation (BP)-based equalization. As a result of having a fully deep learning-based receiver, joint optimization instead of individual optimization of the components is enabled, so-called end-to-end learning. Furthermore, we propose a parallel flooding schedule that further reduces the latency, which turns out to improve also the error correcting performance. The proposed approach is analyzed and compared to state-of-the-art baselines in terms of error correcting capability and latency. At a fixed low latency, the flooding GNN for JED demonstrates a gain of 2.25 dB in bit error rate (BER) compared to an iterative Bahl--Cock--Jelinek--Raviv (BCJR)-BP baseline.

Component Training of Turbo Autoencoders

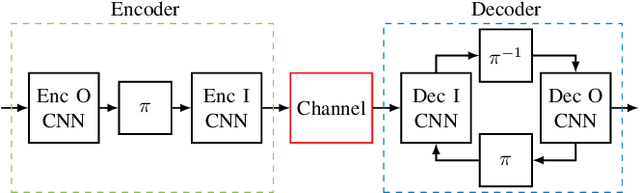
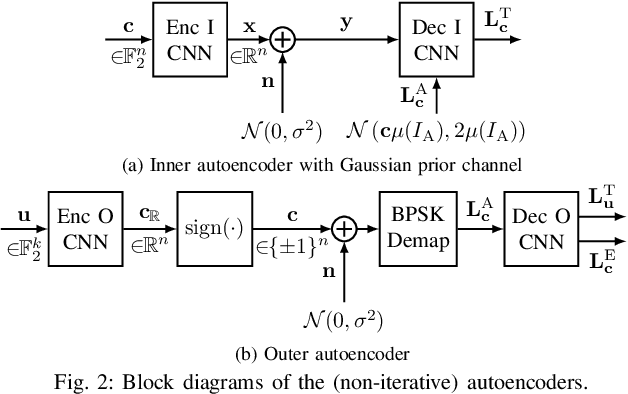
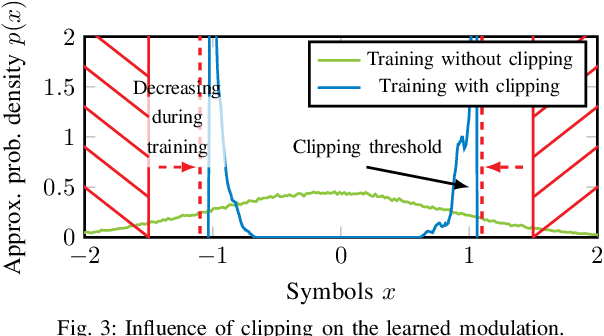
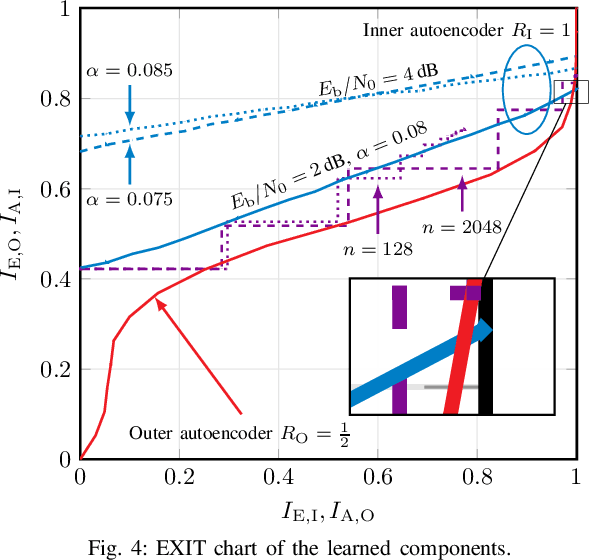
Isolated training with Gaussian priors (TGP) of the component autoencoders of turbo-autoencoder architectures enables faster, more consistent training and better generalization to arbitrary decoding iterations than training based on deep unfolding. We propose fitting the components via extrinsic information transfer (EXIT) charts to a desired behavior which enables scaling to larger message lengths ($k \approx 1000$) while retaining competitive performance. To the best of our knowledge, this is the first autoencoder that performs close to classical codes in this regime. Although the binary cross-entropy (BCE) loss function optimizes the bit error rate (BER) of the components, the design via EXIT charts enables to focus on the block error rate (BLER). In serially concatenated systems the component-wise TGP approach is well known for inner components with a fixed outer binary interface, e.g., a learned inner code or equalizer, with an outer binary error correcting code. In this paper we extend the component training to structures with an inner and outer autoencoder, where we propose a new 1-bit quantization strategy for the encoder outputs based on the underlying communication problem. Finally, we discuss the model complexity of the learned components during design time (training) and inference and show that the number of weights in the encoder can be reduced by 99.96 %.

Optimizing Serially Concatenated Neural Codes with Classical Decoders

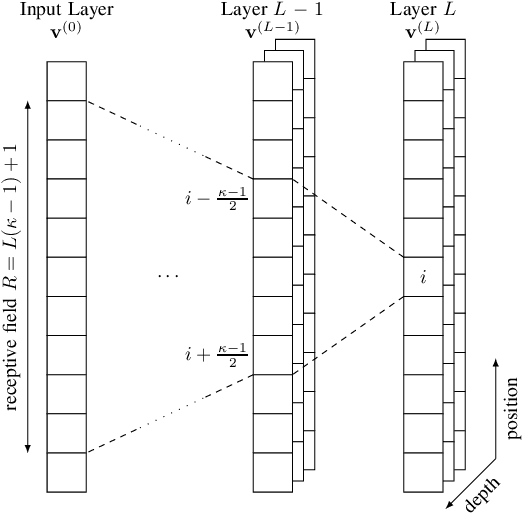
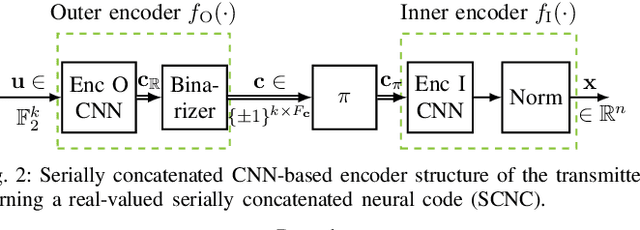
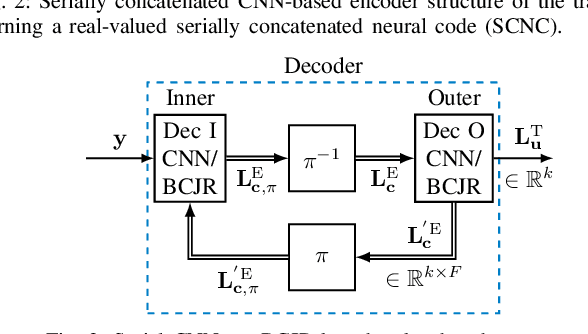
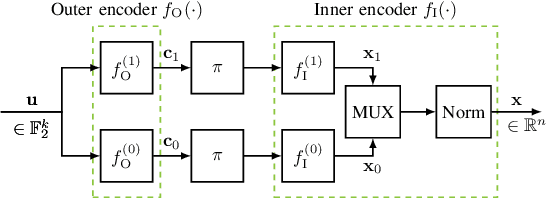
For improving short-length codes, we demonstrate that classic decoders can also be used with real-valued, neural encoders, i.e., deep-learning based codeword sequence generators. Here, the classical decoder can be a valuable tool to gain insights into these neural codes and shed light on weaknesses. Specifically, the turbo-autoencoder is a recently developed channel coding scheme where both encoder and decoder are replaced by neural networks. We first show that the limited receptive field of convolutional neural network (CNN)-based codes enables the application of the BCJR algorithm to optimally decode them with feasible computational complexity. These maximum a posteriori (MAP) component decoders then are used to form classical (iterative) turbo decoders for parallel or serially concatenated CNN encoders, offering a close-to-maximum likelihood (ML) decoding of the learned codes. To the best of our knowledge, this is the first time that a classical decoding algorithm is applied to a non-trivial, real-valued neural code. Furthermore, as the BCJR algorithm is fully differentiable, it is possible to train, or fine-tune, the neural encoder in an end-to-end fashion.

Graph Search based Polar Code Design

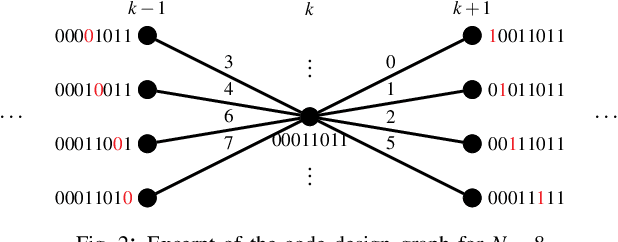
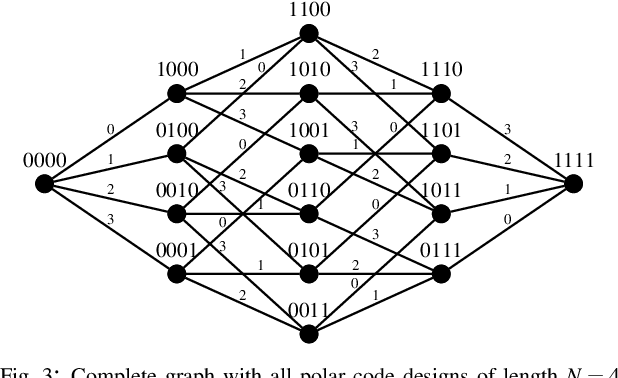
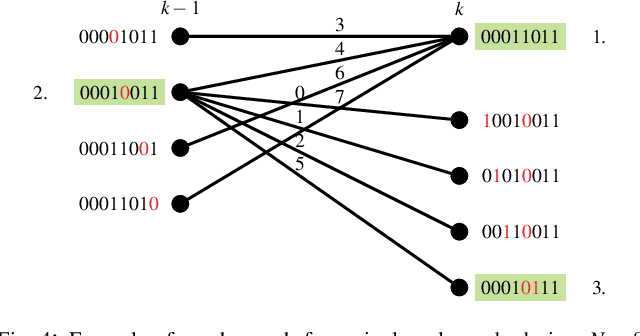
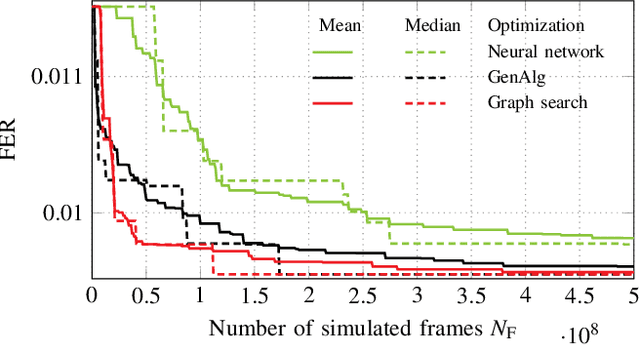
It is well known that to fulfill their full potential, the design of polar codes must be tailored to their intended decoding algorithm. While for successive cancellation (SC) decoding, information theoretically optimal constructions are available, the code design for other decoding algorithms (such as belief propagation (BP) decoding) can only be optimized using extensive Monte Carlo simulations. We propose to view the design process of polar codes as a graph search problem and thereby approaching it more systematically. Based on this formalism, the design-time complexity can be significantly reduced compared to state-of-the-art Genetic Algorithm (GenAlg) and deep learning-based design algorithms. Moreover, sequences of rate-compatible polar codes can be efficiently found. Finally, we analyze both the complexity of the proposed algorithm and the error-rate performance of the constructed codes.

Learning Quantization in LDPC Decoders

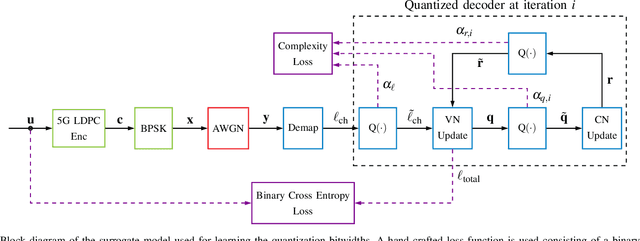
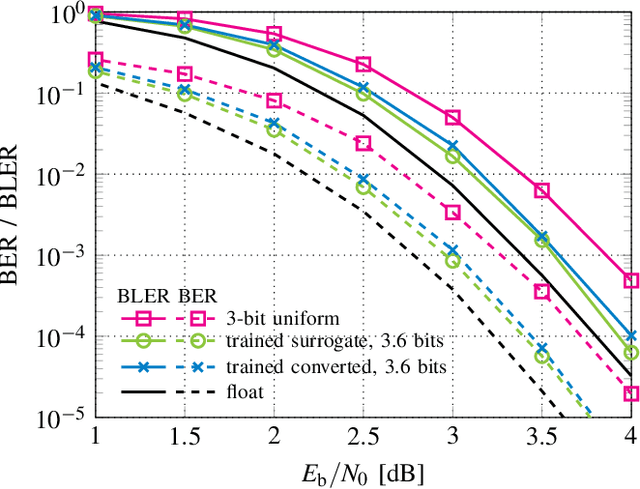
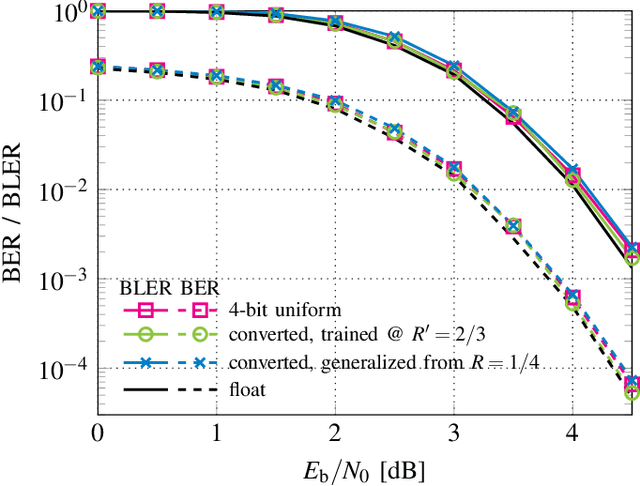
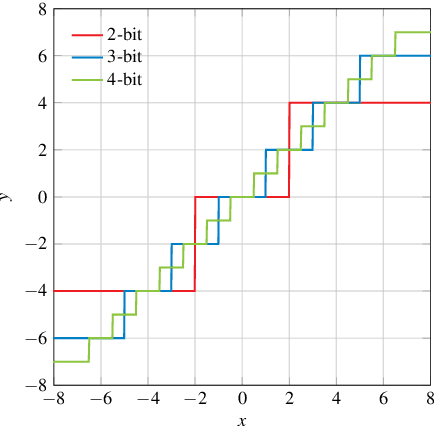
Finding optimal message quantization is a key requirement for low complexity belief propagation (BP) decoding. To this end, we propose a floating-point surrogate model that imitates quantization effects as additions of uniform noise, whose amplitudes are trainable variables. We verify that the surrogate model closely matches the behavior of a fixed-point implementation and propose a hand-crafted loss function to realize a trade-off between complexity and error-rate performance. A deep learning-based method is then applied to optimize the message bitwidths. Moreover, we show that parameter sharing can both ensure implementation-friendly solutions and results in faster training convergence than independent parameters. We provide simulation results for 5G low-density parity-check (LDPC) codes and report an error-rate performance within 0.2 dB of floating-point decoding at an average message quantization bitwidth of 3.1 bits. In addition, we show that the learned bitwidths also generalize to other code rates and channels.