Flexible categorization using formal concept analysis and Dempster-Shafer theory

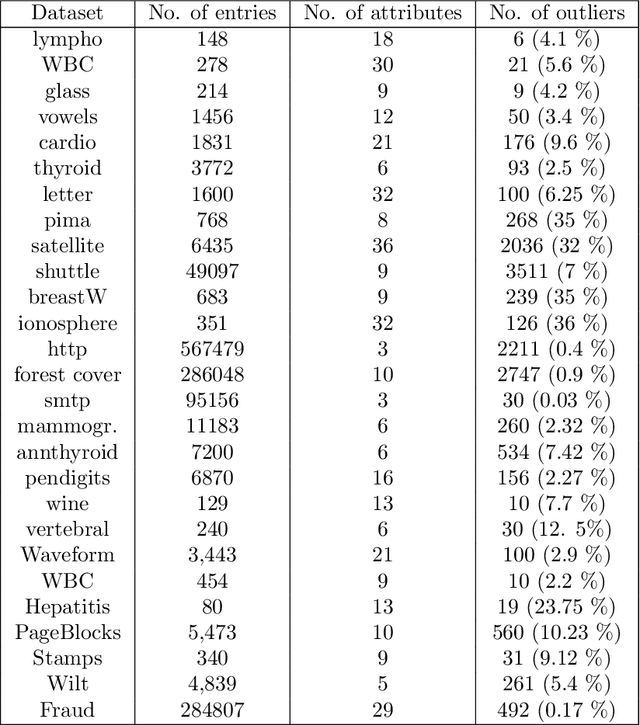
Categorization of business processes is an important part of auditing. Large amounts of transactional data in auditing can be represented as transactions between financial accounts using weighted bipartite graphs. We view such bipartite graphs as many-valued formal contexts, which we use to obtain explainable categorization of these business processes in terms of financial accounts involved in a business process by using methods in formal concept analysis. We use Dempster-Shafer mass functions to represent agendas showing different interest in different set of financial accounts. We also model some possible deliberation scenarios between agents with different interrogative agendas to reach an aggregated agenda and categorization. The framework developed in this paper provides a formal ground to obtain and study explainable categorizations from the data represented as bipartite graphs according to the agendas of different agents in an organization (e.g. an audit firm), and interaction between these through deliberation. We use this framework to describe a machine-leaning meta algorithm for outlier detection and classification which can provide local and global explanations of its result and demonstrate it through an outlier detection algorithm.

Outlier detection using flexible categorisation and interrogative agendas

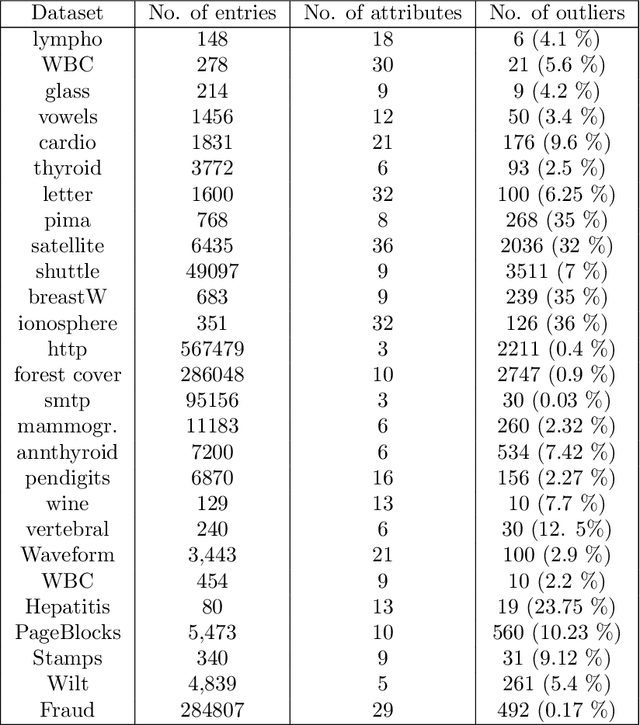
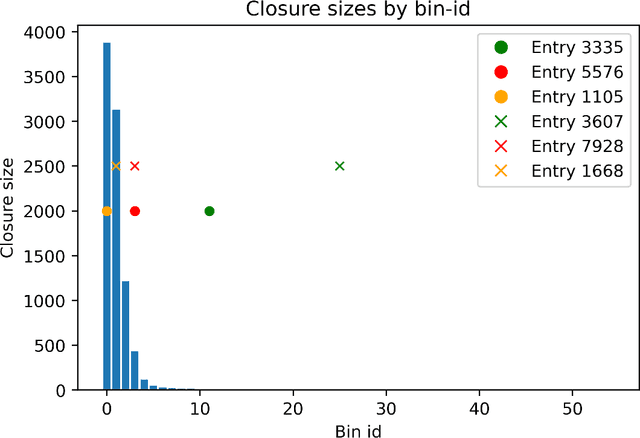
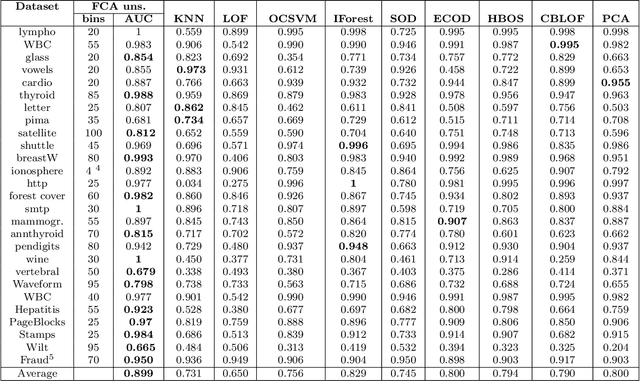
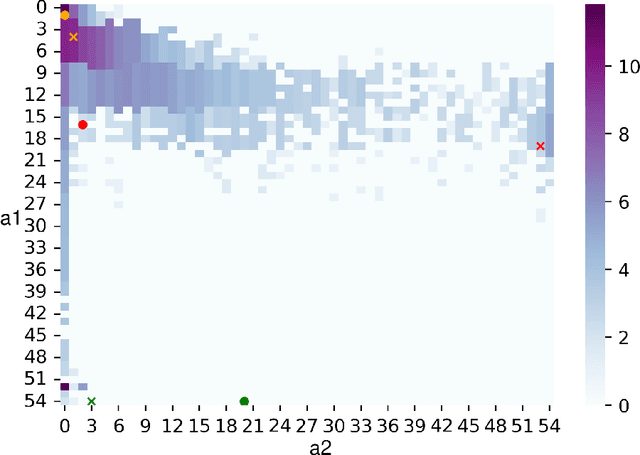
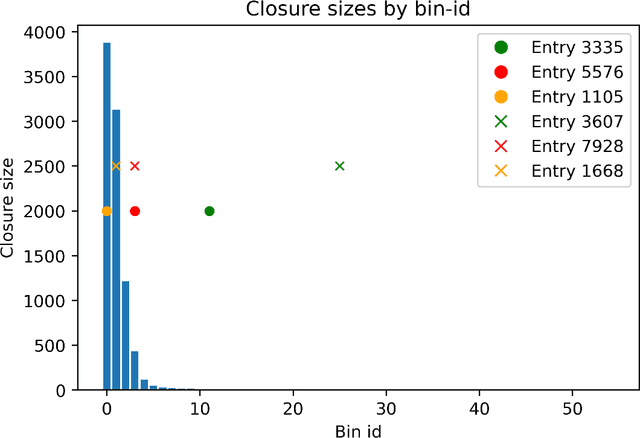
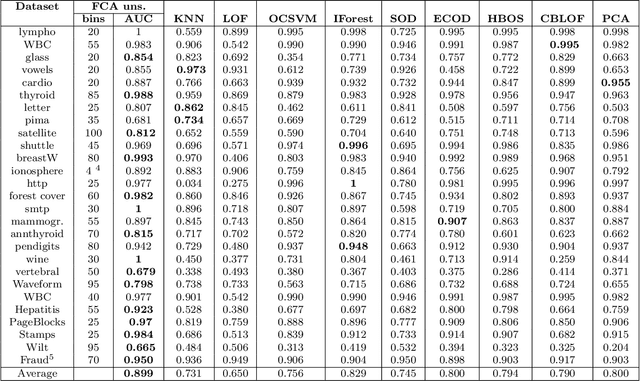
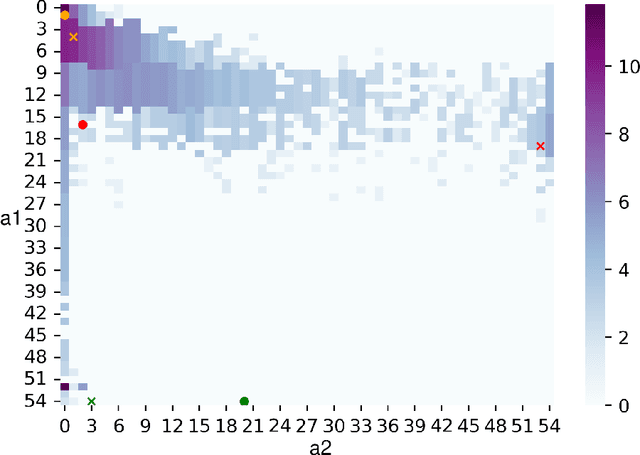
Categorization is one of the basic tasks in machine learning and data analysis. Building on formal concept analysis (FCA), the starting point of the present work is that different ways to categorize a given set of objects exist, which depend on the choice of the sets of features used to classify them, and different such sets of features may yield better or worse categorizations, relative to the task at hand. In their turn, the (a priori) choice of a particular set of features over another might be subjective and express a certain epistemic stance (e.g. interests, relevance, preferences) of an agent or a group of agents, namely, their interrogative agenda. In the present paper, we represent interrogative agendas as sets of features, and explore and compare different ways to categorize objects w.r.t. different sets of features (agendas). We first develop a simple unsupervised FCA-based algorithm for outlier detection which uses categorizations arising from different agendas. We then present a supervised meta-learning algorithm to learn suitable (fuzzy) agendas for categorization as sets of features with different weights or masses. We combine this meta-learning algorithm with the unsupervised outlier detection algorithm to obtain a supervised outlier detection algorithm. We show that these algorithms perform at par with commonly used algorithms for outlier detection on commonly used datasets in outlier detection. These algorithms provide both local and global explanations of their results.

Flexible categorization for auditing using formal concept analysis and Dempster-Shafer theory

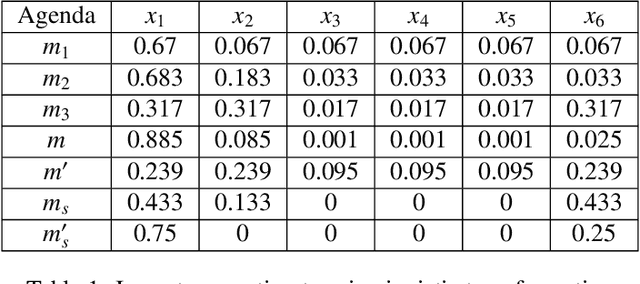
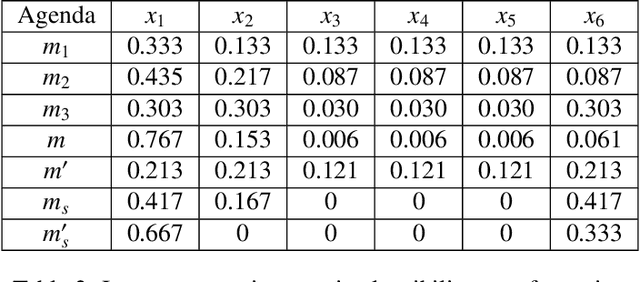
Categorization of business processes is an important part of auditing. Large amounts of transnational data in auditing can be represented as transactions between financial accounts using weighted bipartite graphs. We view such bipartite graphs as many-valued formal contexts, which we use to obtain explainable categorization of these business processes in terms of financial accounts involved in a business process by using methods in formal concept analysis. The specific explainability feature of the methodology introduced in the present paper provides several advantages over e.g.~non-explainable machine learning techniques, and in fact, it can be taken as a basis for the development of algorithms which perform the task of clustering on transparent and accountable principles. Here, we focus on obtaining and studying different ways to categorize according to different extents of interest in different financial accounts, or interrogative agendas, of various agents or sub-tasks in audit. We use Dempster-Shafer mass functions to represent agendas showing different interest in different set of financial accounts. We propose two new methods to obtain categorizations from these agendas. We also model some possible deliberation scenarios between agents with different interrogative agendas to reach an aggregated agenda and categorization. The framework developed in this paper provides a formal ground to obtain and study explainable categorizations from the data represented as bipartite graphs according to the agendas of different agents in an organization (e.g.~an audit firm), and interaction between these through deliberation.

Vector spaces as Kripke frames

In recent years, the compositional distributional approach in computational linguistics has opened the way for an integration of the \emph{lexical} aspects of meaning into Lambek's type-logical grammar program. This approach is based on the observation that a sound semantics for the associative, commutative and unital Lambek calculus can be based on vector spaces by interpreting fusion as the tensor product of vector spaces. In this paper, we build on this observation and extend it to a `vector space semantics' for the {\em general} Lambek calculus, based on {\em algebras over a field} $\mathbb{K}$ (or $\mathbb{K}$-algebras), i.e. vector spaces endowed with a bilinear binary product. Such structures are well known in algebraic geometry and algebraic topology, since they are important instances of Lie algebras and Hopf algebras. Applying results and insights from duality and representation theory for the algebraic semantics of nonclassical logics, we regard $\mathbb{K}$-algebras as `Kripke frames' the complex algebras of which are complete residuated lattices. This perspective makes it possible to establish a systematic connection between vector space semantics and the standard Routley-Meyer semantics of (modal) substructural logics.

Toward a Dempster-Shafer theory of concepts

In this paper, we generalize the basic notions and results of Dempster-Shafer theory from predicates to formal concepts. Results include the representation of conceptual belief functions as inner measures of suitable probability functions, and a Dempster-Shafer rule of combination on belief functions on formal concepts.