Rotation-Invariant Random Features Provide a Strong Baseline for Machine Learning on 3D Point Clouds

Rotational invariance is a popular inductive bias used by many fields in machine learning, such as computer vision and machine learning for quantum chemistry. Rotation-invariant machine learning methods set the state of the art for many tasks, including molecular property prediction and 3D shape classification. These methods generally either rely on task-specific rotation-invariant features, or they use general-purpose deep neural networks which are complicated to design and train. However, it is unclear whether the success of these methods is primarily due to the rotation invariance or the deep neural networks. To address this question, we suggest a simple and general-purpose method for learning rotation-invariant functions of three-dimensional point cloud data using a random features approach. Specifically, we extend the random features method of Rahimi & Recht 2007 by deriving a version that is invariant to three-dimensional rotations and showing that it is fast to evaluate on point cloud data. We show through experiments that our method matches or outperforms the performance of general-purpose rotation-invariant neural networks on standard molecular property prediction benchmark datasets QM7 and QM9. We also show that our method is general-purpose and provides a rotation-invariant baseline on the ModelNet40 shape classification task. Finally, we show that our method has an order of magnitude smaller prediction latency than competing kernel methods.

Von Mises Mixture Distributions for Molecular Conformation Generation

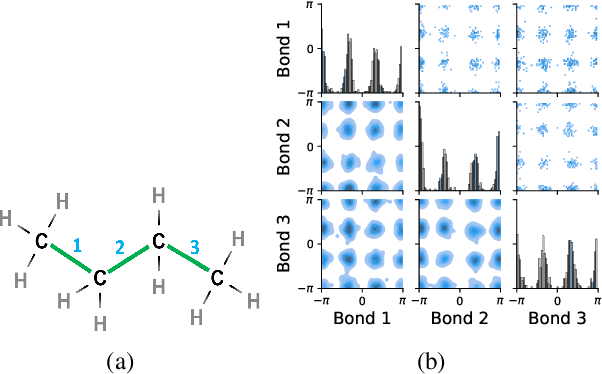
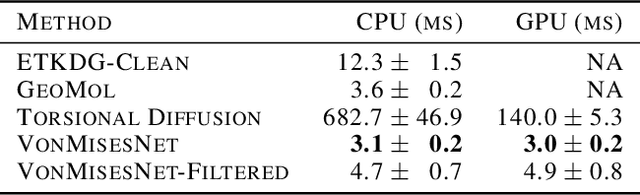
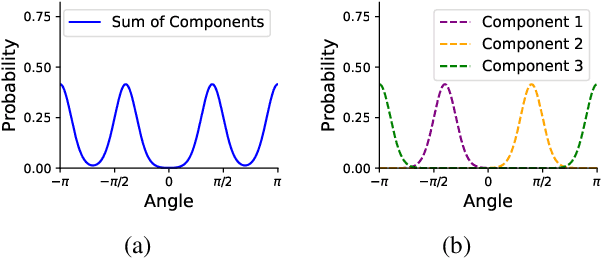
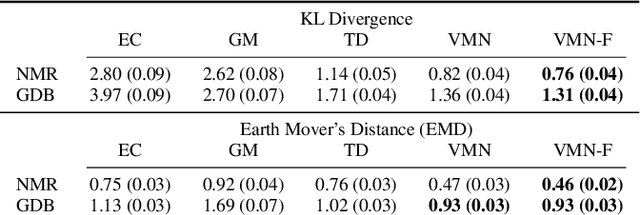
Molecules are frequently represented as graphs, but the underlying 3D molecular geometry (the locations of the atoms) ultimately determines most molecular properties. However, most molecules are not static and at room temperature adopt a wide variety of geometries or $\textit{conformations}$. The resulting distribution on geometries $p(x)$ is known as the Boltzmann distribution, and many molecular properties are expectations computed under this distribution. Generating accurate samples from the Boltzmann distribution is therefore essential for computing these expectations accurately. Traditional sampling-based methods are computationally expensive, and most recent machine learning-based methods have focused on identifying $\textit{modes}$ in this distribution rather than generating true $\textit{samples}$. Generating such samples requires capturing conformational variability, and it has been widely recognized that the majority of conformational variability in molecules arises from rotatable bonds. In this work, we present VonMisesNet, a new graph neural network that captures conformational variability via a variational approximation of rotatable bond torsion angles as a mixture of von Mises distributions. We demonstrate that VonMisesNet can generate conformations for arbitrary molecules in a way that is both physically accurate with respect to the Boltzmann distribution and orders of magnitude faster than existing sampling methods.

Flare Prediction Using Photospheric and Coronal Image Data

The precise physical process that triggers solar flares is not currently understood. Here we attempt to capture the signature of this mechanism in solar image data of various wavelengths and use these signatures to predict flaring activity. We do this by developing an algorithm that [1] automatically generates features in 5.5 TB of image data taken by the Solar Dynamics Observatory of the solar photosphere, chromosphere, transition region, and corona during the time period between May 2010 and May 2014, [2] combines these features with other features based on flaring history and a physical understanding of putative flaring processes, and [3] classifies these features to predict whether a solar active region will flare within a time period of $T$ hours, where $T$ = 2 and 24. We find that when optimizing for the True Skill Score (TSS), photospheric vector magnetic field data combined with flaring history yields the best performance, and when optimizing for the area under the precision-recall curve, all the data are helpful. Our model performance yields a TSS of $0.84 \pm 0.03$ and $0.81 \pm 0.03$ in the $T$ = 2 and 24 hour cases, respectively, and a value of $0.13 \pm 0.07$ and $0.43 \pm 0.08$ for the area under the precision-recall curve in the $T$ = 2 and 24 hour cases, respectively. These relatively high scores are similar to, but not greater than, other attempts to predict solar flares. Given the similar values of algorithm performance across various types of models reported in the literature, we conclude that we can expect a certain baseline predictive capacity using these data. This is the first attempt to predict solar flares using photospheric vector magnetic field data as well as multiple wavelengths of image data from the chromosphere, transition region, and corona.

CrossCat: A Fully Bayesian Nonparametric Method for Analyzing Heterogeneous, High Dimensional Data

There is a widespread need for statistical methods that can analyze high-dimensional datasets with- out imposing restrictive or opaque modeling assumptions. This paper describes a domain-general data analysis method called CrossCat. CrossCat infers multiple non-overlapping views of the data, each consisting of a subset of the variables, and uses a separate nonparametric mixture to model each view. CrossCat is based on approximately Bayesian inference in a hierarchical, nonparamet- ric model for data tables. This model consists of a Dirichlet process mixture over the columns of a data table in which each mixture component is itself an independent Dirichlet process mixture over the rows; the inner mixture components are simple parametric models whose form depends on the types of data in the table. CrossCat combines strengths of mixture modeling and Bayesian net- work structure learning. Like mixture modeling, CrossCat can model a broad class of distributions by positing latent variables, and produces representations that can be efficiently conditioned and sampled from for prediction. Like Bayesian networks, CrossCat represents the dependencies and independencies between variables, and thus remains accurate when there are multiple statistical signals. Inference is done via a scalable Gibbs sampling scheme; this paper shows that it works well in practice. This paper also includes empirical results on heterogeneous tabular data of up to 10 million cells, such as hospital cost and quality measures, voting records, unemployment rates, gene expression measurements, and images of handwritten digits. CrossCat infers structure that is consistent with accepted findings and common-sense knowledge in multiple domains and yields predictive accuracy competitive with generative, discriminative, and model-free alternatives.

Automatic discovery of cell types and microcircuitry from neural connectomics

Neural connectomics has begun producing massive amounts of data, necessitating new analysis methods to discover the biological and computational structure. It has long been assumed that discovering neuron types and their relation to microcircuitry is crucial to understanding neural function. Here we developed a nonparametric Bayesian technique that identifies neuron types and microcircuitry patterns in connectomics data. It combines the information traditionally used by biologists, including connectivity, cell body location and the spatial distribution of synapses, in a principled and probabilistically-coherent manner. We show that the approach recovers known neuron types in the retina and enables predictions of connectivity, better than simpler algorithms. It also can reveal interesting structure in the nervous system of C. elegans, and automatically discovers the structure of a microprocessor. Our approach extracts structural meaning from connectomics, enabling new approaches of automatically deriving anatomical insights from these emerging datasets.

Scaling Nonparametric Bayesian Inference via Subsample-Annealing

We describe an adaptation of the simulated annealing algorithm to nonparametric clustering and related probabilistic models. This new algorithm learns nonparametric latent structure over a growing and constantly churning subsample of training data, where the portion of data subsampled can be interpreted as the inverse temperature beta(t) in an annealing schedule. Gibbs sampling at high temperature (i.e., with a very small subsample) can more quickly explore sketches of the final latent state by (a) making longer jumps around latent space (as in block Gibbs) and (b) lowering energy barriers (as in simulated annealing). We prove subsample annealing speeds up mixing time N^2 -> N in a simple clustering model and exp(N) -> N in another class of models, where N is data size. Empirically subsample-annealing outperforms naive Gibbs sampling in accuracy-per-wallclock time, and can scale to larger datasets and deeper hierarchical models. We demonstrate improved inference on million-row subsamples of US Census data and network log data and a 307-row hospital rating dataset, using a Pitman-Yor generalization of the Cross Categorization model.

Building fast Bayesian computing machines out of intentionally stochastic, digital parts

The brain interprets ambiguous sensory information faster and more reliably than modern computers, using neurons that are slower and less reliable than logic gates. But Bayesian inference, which underpins many computational models of perception and cognition, appears computationally challenging even given modern transistor speeds and energy budgets. The computational principles and structures needed to narrow this gap are unknown. Here we show how to build fast Bayesian computing machines using intentionally stochastic, digital parts, narrowing this efficiency gap by multiple orders of magnitude. We find that by connecting stochastic digital components according to simple mathematical rules, one can build massively parallel, low precision circuits that solve Bayesian inference problems and are compatible with the Poisson firing statistics of cortical neurons. We evaluate circuits for depth and motion perception, perceptual learning and causal reasoning, each performing inference over 10,000+ latent variables in real time - a 1,000x speed advantage over commodity microprocessors. These results suggest a new role for randomness in the engineering and reverse-engineering of intelligent computation.