Von Mises Mixture Distributions for Molecular Conformation Generation
Paper and Code
Jun 13, 2023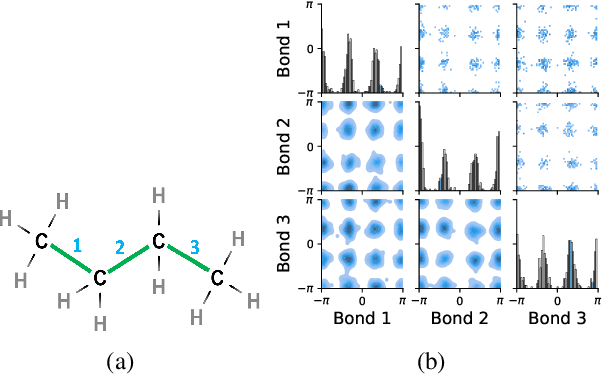
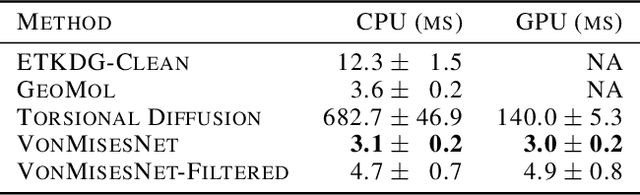
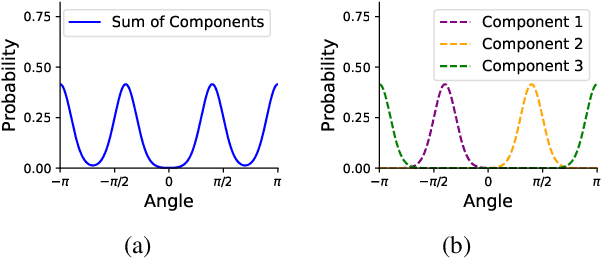
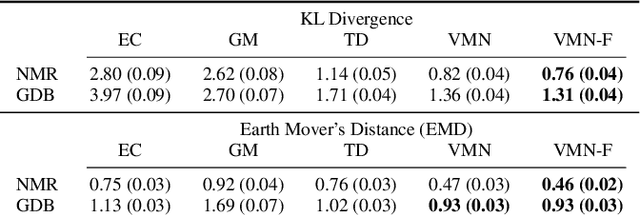
Molecules are frequently represented as graphs, but the underlying 3D molecular geometry (the locations of the atoms) ultimately determines most molecular properties. However, most molecules are not static and at room temperature adopt a wide variety of geometries or $\textit{conformations}$. The resulting distribution on geometries $p(x)$ is known as the Boltzmann distribution, and many molecular properties are expectations computed under this distribution. Generating accurate samples from the Boltzmann distribution is therefore essential for computing these expectations accurately. Traditional sampling-based methods are computationally expensive, and most recent machine learning-based methods have focused on identifying $\textit{modes}$ in this distribution rather than generating true $\textit{samples}$. Generating such samples requires capturing conformational variability, and it has been widely recognized that the majority of conformational variability in molecules arises from rotatable bonds. In this work, we present VonMisesNet, a new graph neural network that captures conformational variability via a variational approximation of rotatable bond torsion angles as a mixture of von Mises distributions. We demonstrate that VonMisesNet can generate conformations for arbitrary molecules in a way that is both physically accurate with respect to the Boltzmann distribution and orders of magnitude faster than existing sampling methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge