Quantum-Assisted Automatic Path-Planning for Robotic Quality Inspection in Industry 4.0

This work explores the application of hybrid quantum-classical algorithms to optimize robotic inspection trajectories derived from Computer-Aided Design (CAD) models in industrial settings. By modeling the task as a 3D variant of the Traveling Salesman Problem, incorporating incomplete graphs and open-route constraints, this study evaluates the performance of two D-Wave-based solvers against classical methods such as GUROBI and Google OR-Tools. Results across five real-world cases demonstrate competitive solution quality with significantly reduced computation times, highlighting the potential of quantum approaches in automation under Industry 4.0.

Addressing the Minor-Embedding Problem in Quantum Annealing and Evaluating State-of-the-Art Algorithm Performance

This study addresses the minor-embedding problem, which involves mapping the variables of an Ising model onto a quantum annealing processor. The primary motivation stems from the observed performance disparity of quantum annealers when solving problems suited to the processor's architecture versus those with non-hardware-native topologies. Our research has two main objectives: i) to analyze the impact of embedding quality on the performance of D-Wave Systems quantum annealers, and ii) to evaluate the quality of the embeddings generated by Minorminer, an algorithm provided by D-Wave and widely recognized as the standard minor-embedding technique in the literature. Regarding the first objective, our experiments reveal a clear correlation between the average chain length of embeddings and the relative errors of the solutions sampled. This underscores the critical influence of embedding quality on quantum annealing performance. For the second objective, we focus on the Minorminer technique, assessing its capacity to embed problems, the quality of the embeddings produced, and the robustness of the results. We also compare its performance with Clique Embedding, another algorithm developed by D-Wave, which is deterministic and designed to embed fully connected Ising models into quantum annealing processors, serving as a worst-case scenario. The results demonstrate that there is significant room for improvement for Minorminer, as it has not consistently outperformed the worst-case scenario.

Steiner Traveling Salesman Problem with Quantum Annealing

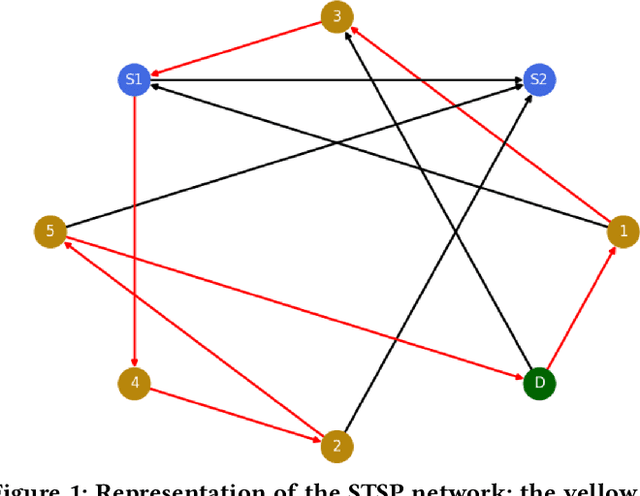
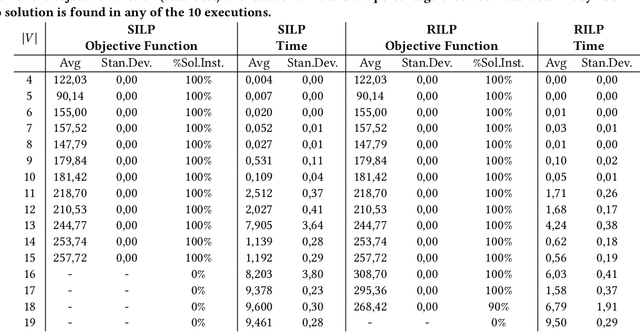
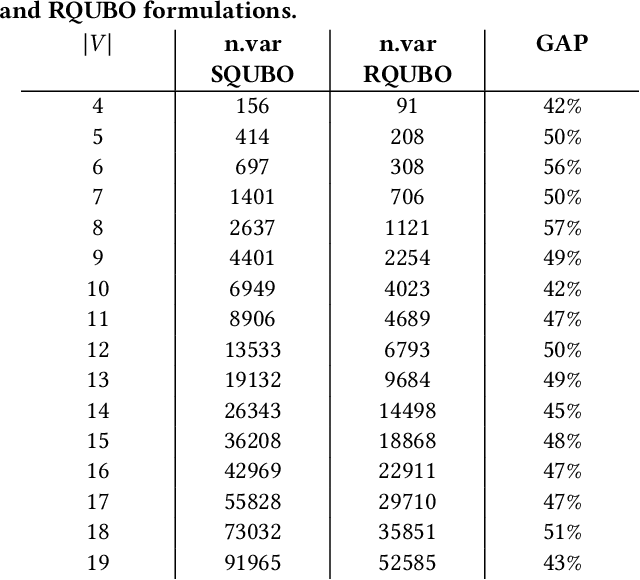
The Steiner Traveling Salesman Problem (STSP) is a variant of the classical Traveling Salesman Problem. The STSP involves incorporating steiner nodes, which are extra nodes not originally part of the required visit set but that can be added to the route to enhance the overall solution and minimize the total travel cost. Given the NP-hard nature of the STSP, we propose a quantum approach to address it. Specifically, we employ quantum annealing using D-Wave's hardware to explore its potential for solving this problem. To enhance computational feasibility, we develop a preprocessing method that effectively reduces the network size. Our experimental results demonstrate that this reduction technique significantly decreases the problem complexity, making the Quadratic Unconstrained Binary Optimization formulation, the standard input for quantum annealers, better suited for existing quantum hardware. Furthermore, the results highlight the potential of quantum annealing as a promising and innovative approach for solving the STSP.

Optimizing Package Delivery with Quantum Annealers: Addressing Time-Windows and Simultaneous Pickup and Delivery

Recent research at the intersection of quantum computing and routing problems has been highly prolific. Much of this work focuses on classical problems such as the Traveling Salesman Problem and the Vehicle Routing Problem. The practical applicability of these problems depends on the specific objectives and constraints considered. However, it is undeniable that translating complex real-world requirements into these classical formulations often proves challenging. In this paper, we resort to our previously published quantum-classical technique for addressing real-world-oriented routing problems, known as Quantum for Real Package Delivery (Q4RPD), and elaborate on solving additional realistic problem instances. Accordingly, this paper emphasizes the following characteristics: i) simultaneous pickup and deliveries, ii) time-windows, and iii) mobility restrictions by vehicle type. To illustrate the application of Q4RPD, we have conducted an experimentation comprising seven instances, serving as a demonstration of the newly developed features.

Solving Drone Routing Problems with Quantum Computing: A Hybrid Approach Combining Quantum Annealing and Gate-Based Paradigms

This paper presents a novel hybrid approach to solving real-world drone routing problems by leveraging the capabilities of quantum computing. The proposed method, coined Quantum for Drone Routing (Q4DR), integrates the two most prominent paradigms in the field: quantum gate-based computing, through the Eclipse Qrisp programming language; and quantum annealers, by means of D-Wave System's devices. The algorithm is divided into two different phases: an initial clustering phase executed using a Quantum Approximate Optimization Algorithm (QAOA), and a routing phase employing quantum annealers. The efficacy of Q4DR is demonstrated through three use cases of increasing complexity, each incorporating real-world constraints such as asymmetric costs, forbidden paths, and itinerant charging points. This research contributes to the growing body of work in quantum optimization, showcasing the practical applications of quantum computing in logistics and route planning.

Transfer of Knowledge through Reverse Annealing: A Preliminary Analysis of the Benefits and What to Share

Being immersed in the NISQ-era, current quantum annealers present limitations for solving optimization problems efficiently. To mitigate these limitations, D-Wave Systems developed a mechanism called Reverse Annealing, a specific type of quantum annealing designed to perform local refinement of good states found elsewhere. Despite the research activity around Reverse Annealing, none has theorized about the possible benefits related to the transfer of knowledge under this paradigm. This work moves in that direction and is driven by experimentation focused on answering two key research questions: i) is reverse annealing a paradigm that can benefit from knowledge transfer between similar problems? and ii) can we infer the characteristics that an input solution should meet to help increase the probability of success? To properly guide the tests in this paper, the well-known Knapsack Problem has been chosen for benchmarking purposes, using a total of 34 instances composed of 14 and 16 items.

On the Transfer of Knowledge in Quantum Algorithms

The field of quantum computing is generating significant anticipation within the scientific and industrial communities due to its potential to revolutionize computing paradigms. Recognizing this potential, this paper explores the integration of transfer of knowledge techniques, traditionally used in classical artificial intelligence, into quantum computing. We present a comprehensive classification of the transfer models, focusing on Transfer Learning and Transfer Optimization. Additionally, we analyze relevant schemes in quantum computing that can benefit from knowledge sharing, and we delve into the potential synergies, supported by theoretical insights and initial experimental results. Our findings suggest that leveraging the transfer of knowledge can enhance the efficiency and effectiveness of quantum algorithms, particularly in the context of hybrid solvers. This approach not only accelerates the optimization process but also reduces the computational burden on quantum processors, making it a valuable tool for advancing quantum computing technologies.

D-Wave's Nonlinear-Program Hybrid Solver: Description and Performance Analysis

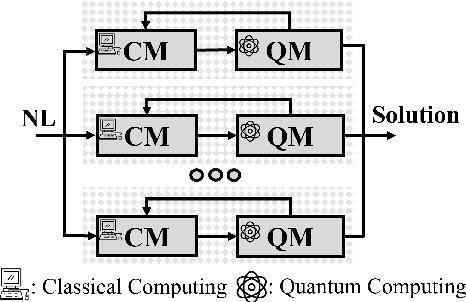
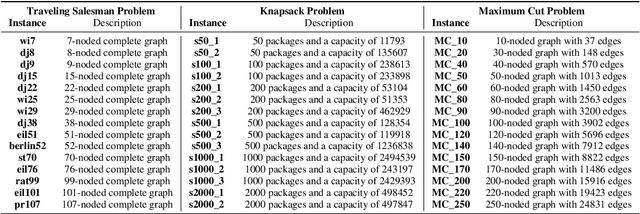
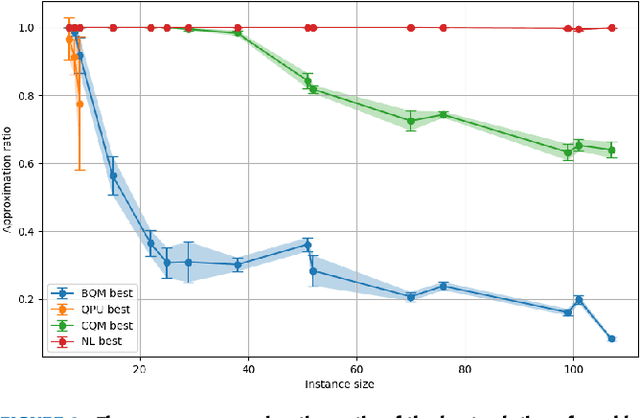
The development of advanced quantum-classical algorithms is among the most prominent strategies in quantum computing. Numerous hybrid solvers have been introduced recently. Many of these methods are created ad hoc to address specific use cases. However, several well-established schemes are frequently utilized to address optimization problems. In this context, D-Wave launched the Hybrid Solver Service in 2020, offering a portfolio of methods designed to accelerate time-to-solution for users aiming to optimize performance and operational processes. Recently, a new technique has been added to this portfolio: the Nonlinear-Program Hybrid Solver. This paper describes this solver and evaluates its performance through a benchmark of 45 instances across three combinatorial optimization problems: the Traveling Salesman Problem, the Knapsack Problem, and the Maximum Cut Problem. To facilitate the use of this relatively unexplored solver, we provide details of the implementation used to solve these three optimization problems.

A Tutorial on the Design, Experimentation and Application of Metaheuristic Algorithms to Real-World Optimization Problems

In the last few years, the formulation of real-world optimization problems and their efficient solution via metaheuristic algorithms has been a catalyst for a myriad of research studies. In spite of decades of historical advancements on the design and use of metaheuristics, large difficulties still remain in regards to the understandability, algorithmic design uprightness, and performance verifiability of new technical achievements. A clear example stems from the scarce replicability of works dealing with metaheuristics used for optimization, which is often infeasible due to ambiguity and lack of detail in the presentation of the methods to be reproduced. Additionally, in many cases, there is a questionable statistical significance of their reported results. This work aims at providing the audience with a proposal of good practices which should be embraced when conducting studies about metaheuristics methods used for optimization in order to provide scientific rigor, value and transparency. To this end, we introduce a step by step methodology covering every research phase that should be followed when addressing this scientific field. Specifically, frequently overlooked yet crucial aspects and useful recommendations will be discussed in regards to the formulation of the problem, solution encoding, implementation of search operators, evaluation metrics, design of experiments, and considerations for real-world performance, among others. Finally, we will outline important considerations, challenges, and research directions for the success of newly developed optimization metaheuristics in their deployment and operation over real-world application environments.

Exploring Utility in a Real-World Warehouse Optimization Problem: Formulation Based on Quantun Annealers and Preliminary Results

In the current NISQ-era, one of the major challenges faced by researchers and practitioners lies in figuring out how to combine quantum and classical computing in the most efficient and innovative way. In this paper, we present a mechanism coined as Quantum Initialization for Warehouse Optimization Problem that resorts to D-Wave's Quantum Annealer. The module has been specifically designed to be embedded into already existing classical software dedicated to the optimization of a real-world industrial problem. We preliminary tested the implemented mechanism through a two-phase experiment against the classical version of the software.