Solving Drone Routing Problems with Quantum Computing: A Hybrid Approach Combining Quantum Annealing and Gate-Based Paradigms

This paper presents a novel hybrid approach to solving real-world drone routing problems by leveraging the capabilities of quantum computing. The proposed method, coined Quantum for Drone Routing (Q4DR), integrates the two most prominent paradigms in the field: quantum gate-based computing, through the Eclipse Qrisp programming language; and quantum annealers, by means of D-Wave System's devices. The algorithm is divided into two different phases: an initial clustering phase executed using a Quantum Approximate Optimization Algorithm (QAOA), and a routing phase employing quantum annealers. The efficacy of Q4DR is demonstrated through three use cases of increasing complexity, each incorporating real-world constraints such as asymmetric costs, forbidden paths, and itinerant charging points. This research contributes to the growing body of work in quantum optimization, showcasing the practical applications of quantum computing in logistics and route planning.

Non-Convergence and Limit Cycles in the Adam optimizer

One of the most popular training algorithms for deep neural networks is the Adaptive Moment Estimation (Adam) introduced by Kingma and Ba. Despite its success in many applications there is no satisfactory convergence analysis: only local convergence can be shown for batch mode under some restrictions on the hyperparameters, counterexamples exist for incremental mode. Recent results show that for simple quadratic objective functions limit cycles of period 2 exist in batch mode, but only for atypical hyperparameters, and only for the algorithm without bias correction. %More general there are several more adaptive gradient methods which try to estimate a fitting learning rate and / or search direction from the training data to improve the learning process compared to pure gradient descent with fixed learningrate. We extend the convergence analysis for Adam in the batch mode with bias correction and show that even for quadratic objective functions as the simplest case of convex functions 2-limit-cycles exist, for all choices of the hyperparameters. We analyze the stability of these limit cycles and relate our analysis to other results where approximate convergence was shown, but under the additional assumption of bounded gradients which does not apply to quadratic functions. The investigation heavily relies on the use of computer algebra due to the complexity of the equations.

Local Convergence of Adaptive Gradient Descent Optimizers

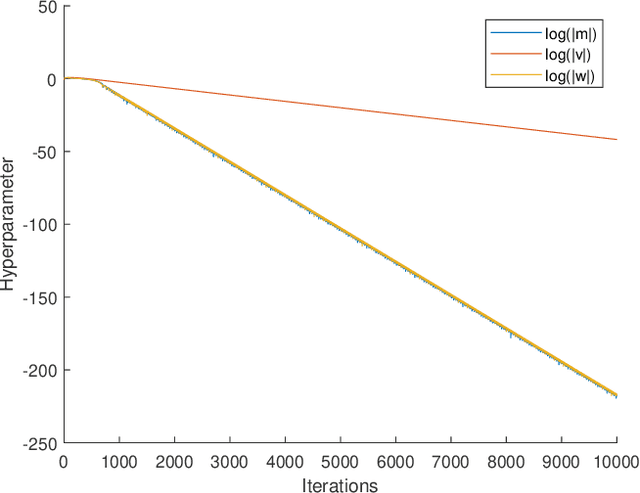
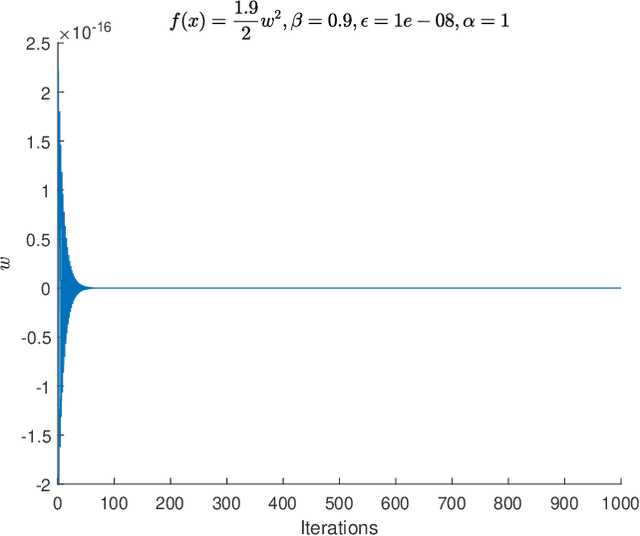
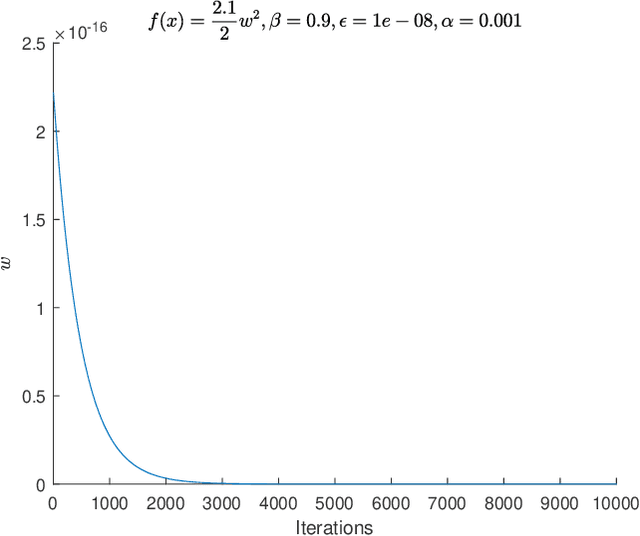
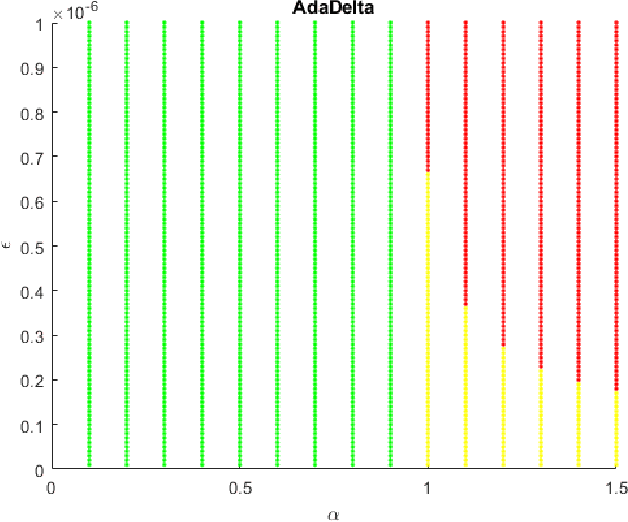
Adaptive Moment Estimation (ADAM) is a very popular training algorithm for deep neural networks and belongs to the family of adaptive gradient descent optimizers. However to the best of the authors knowledge no complete convergence analysis exists for ADAM. The contribution of this paper is a method for the local convergence analysis in batch mode for a deterministic fixed training set, which gives necessary conditions for the hyperparameters of the ADAM algorithm. Due to the local nature of the arguments the objective function can be non-convex but must be at least twice continuously differentiable. Then we apply this procedure to other adaptive gradient descent algorithms and show for most of them local convergence with hyperparameter bounds.

An improvement of the convergence proof of the ADAM-Optimizer

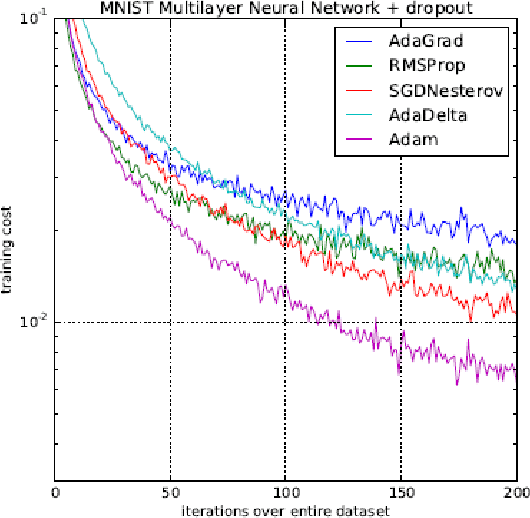
A common way to train neural networks is the Backpropagation. This algorithm includes a gradient descent method, which needs an adaptive step size. In the area of neural networks, the ADAM-Optimizer is one of the most popular adaptive step size methods. It was invented in \cite{Kingma.2015} by Kingma and Ba. The $5865$ citations in only three years shows additionally the importance of the given paper. We discovered that the given convergence proof of the optimizer contains some mistakes, so that the proof will be wrong. In this paper we give an improvement to the convergence proof of the ADAM-Optimizer.