Optimal Object Placement using a Virtual Axis

A basic task in the design of a robotic production cell is the relative placement of robot and workpiece. The fundamental requirement is that the robot can reach all process positions; only then one can think of further optimization. Therefore an algorithm that automatically places an object into the workspace is very desirable. However many iterative optimzation algorithms cannot guarantee that all intermediate steps are reachable, resulting in complicated procedures. We present a novel approach which extends a robot by a virtual prismatic joint - which measures the distance to the workspace - such that any TCP frames are reachable. This allows higher order nonlinear programming algorithms to be used for placement of an object alone as well as the optimal placement under some differentiable criterion.

Optimization of Robot Tasks with Cartesian Degrees of Freedom using Virtual Joints

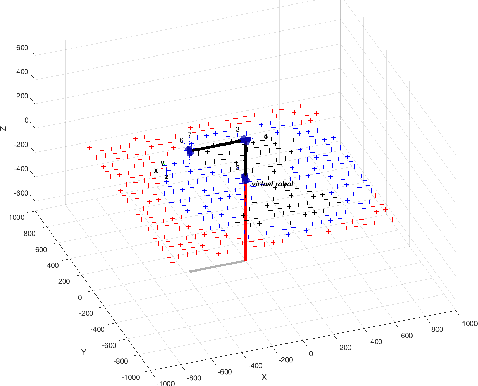
A common task in robotics is unloading identical goods from a tray with rectangular grid structure. This naturally leads to the idea of programming the process at one grid position only and translating the motion to the other grid points, saving teaching time. However this approach usually fails because of joint limits or singularities of the robot. If the task description has some redundancies, e.g. the objects are cylinders where one orientation angle is free for the gripping process, the motion may be modified to avoid workspace problems. We present a mathematical algorithm that allows the automatic generation of robot programs for pick-and-place applications with structured positions when the workpieces have some symmetry, resulting in a Cartesian degree of freedom for the process. The optimization uses the idea of a virtual joint which measures the distance of the desired TCP to the workspace such that the nonlinear optimization method is not bothered with unreachable positions. Combined with smoothed versions of the functions in the nonlinear program higher order algorithms can be used, with theoretical justification superior to many ad-hoc approaches used so far.

An improvement of the convergence proof of the ADAM-Optimizer

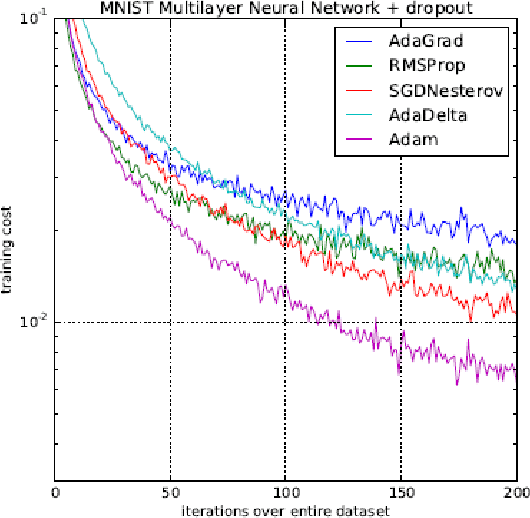
A common way to train neural networks is the Backpropagation. This algorithm includes a gradient descent method, which needs an adaptive step size. In the area of neural networks, the ADAM-Optimizer is one of the most popular adaptive step size methods. It was invented in \cite{Kingma.2015} by Kingma and Ba. The $5865$ citations in only three years shows additionally the importance of the given paper. We discovered that the given convergence proof of the optimizer contains some mistakes, so that the proof will be wrong. In this paper we give an improvement to the convergence proof of the ADAM-Optimizer.