Solving Drone Routing Problems with Quantum Computing: A Hybrid Approach Combining Quantum Annealing and Gate-Based Paradigms

This paper presents a novel hybrid approach to solving real-world drone routing problems by leveraging the capabilities of quantum computing. The proposed method, coined Quantum for Drone Routing (Q4DR), integrates the two most prominent paradigms in the field: quantum gate-based computing, through the Eclipse Qrisp programming language; and quantum annealers, by means of D-Wave System's devices. The algorithm is divided into two different phases: an initial clustering phase executed using a Quantum Approximate Optimization Algorithm (QAOA), and a routing phase employing quantum annealers. The efficacy of Q4DR is demonstrated through three use cases of increasing complexity, each incorporating real-world constraints such as asymmetric costs, forbidden paths, and itinerant charging points. This research contributes to the growing body of work in quantum optimization, showcasing the practical applications of quantum computing in logistics and route planning.

D-Wave's Nonlinear-Program Hybrid Solver: Description and Performance Analysis

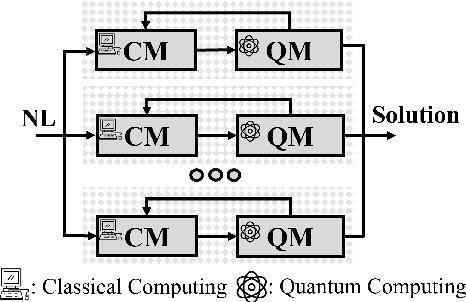
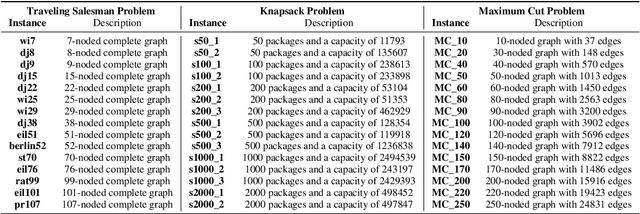
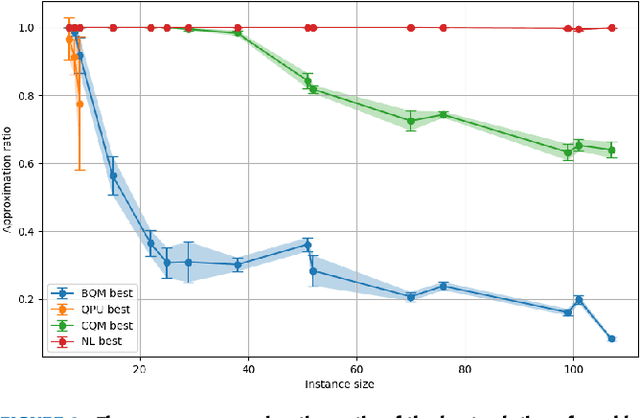
The development of advanced quantum-classical algorithms is among the most prominent strategies in quantum computing. Numerous hybrid solvers have been introduced recently. Many of these methods are created ad hoc to address specific use cases. However, several well-established schemes are frequently utilized to address optimization problems. In this context, D-Wave launched the Hybrid Solver Service in 2020, offering a portfolio of methods designed to accelerate time-to-solution for users aiming to optimize performance and operational processes. Recently, a new technique has been added to this portfolio: the Nonlinear-Program Hybrid Solver. This paper describes this solver and evaluates its performance through a benchmark of 45 instances across three combinatorial optimization problems: the Traveling Salesman Problem, the Knapsack Problem, and the Maximum Cut Problem. To facilitate the use of this relatively unexplored solver, we provide details of the implementation used to solve these three optimization problems.