Emiliano Dall'Anese
Online Learning with Probing for Sequential User-Centric Selection
Jul 27, 2025
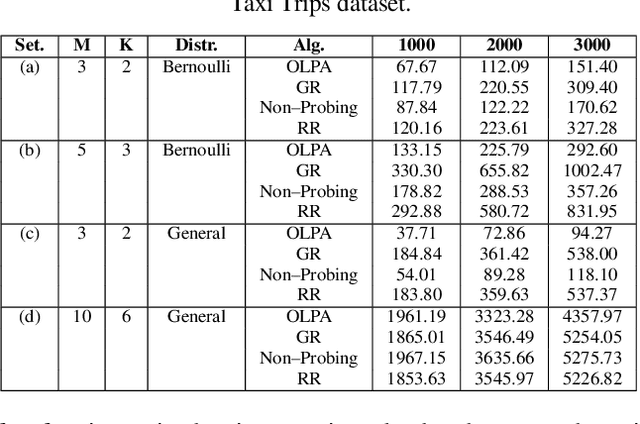

Abstract:We formalize sequential decision-making with information acquisition as the probing-augmented user-centric selection (PUCS) framework, where a learner first probes a subset of arms to obtain side information on resources and rewards, and then assigns $K$ plays to $M$ arms. PUCS covers applications such as ridesharing, wireless scheduling, and content recommendation, in which both resources and payoffs are initially unknown and probing is costly. For the offline setting with known distributions, we present a greedy probing algorithm with a constant-factor approximation guarantee $\zeta = (e-1)/(2e-1)$. For the online setting with unknown distributions, we introduce OLPA, a stochastic combinatorial bandit algorithm that achieves a regret bound $\mathcal{O}(\sqrt{T} + \ln^{2} T)$. We also prove a lower bound $\Omega(\sqrt{T})$, showing that the upper bound is tight up to logarithmic factors. Experiments on real-world data demonstrate the effectiveness of our solutions.
Neural Network-assisted Interval Reachability for Systems with Control Barrier Function-Based Safe Controllers
Apr 11, 2025Abstract:Control Barrier Functions (CBFs) have been widely utilized in the design of optimization-based controllers and filters for dynamical systems to ensure forward invariance of a given set of safe states. While CBF-based controllers offer safety guarantees, they can compromise the performance of the system, leading to undesirable behaviors such as unbounded trajectories and emergence of locally stable spurious equilibria. Computing reachable sets for systems with CBF-based controllers is an effective approach for runtime performance and stability verification, and can potentially serve as a tool for trajectory re-planning. In this paper, we propose a computationally efficient interval reachability method for performance verification of systems with optimization-based controllers by: (i) approximating the optimization-based controller by a pre-trained neural network to avoid solving optimization problems repeatedly, and (ii) using mixed monotone theory to construct an embedding system that leverages state-of-the-art neural network verification algorithms for bounding the output of the neural network. Results in terms of closeness of solutions of trajectories of the system with the optimization-based controller and the neural network are derived. Using a single trajectory of the embedding system along with our closeness of solutions result, we obtain an over-approximation of the reachable set of the system with optimization-based controllers. Numerical results are presented to corroborate the technical findings.
Online Weak-form Sparse Identification of Partial Differential Equations
Mar 08, 2022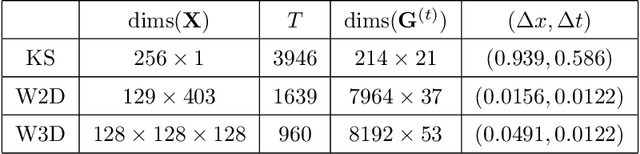
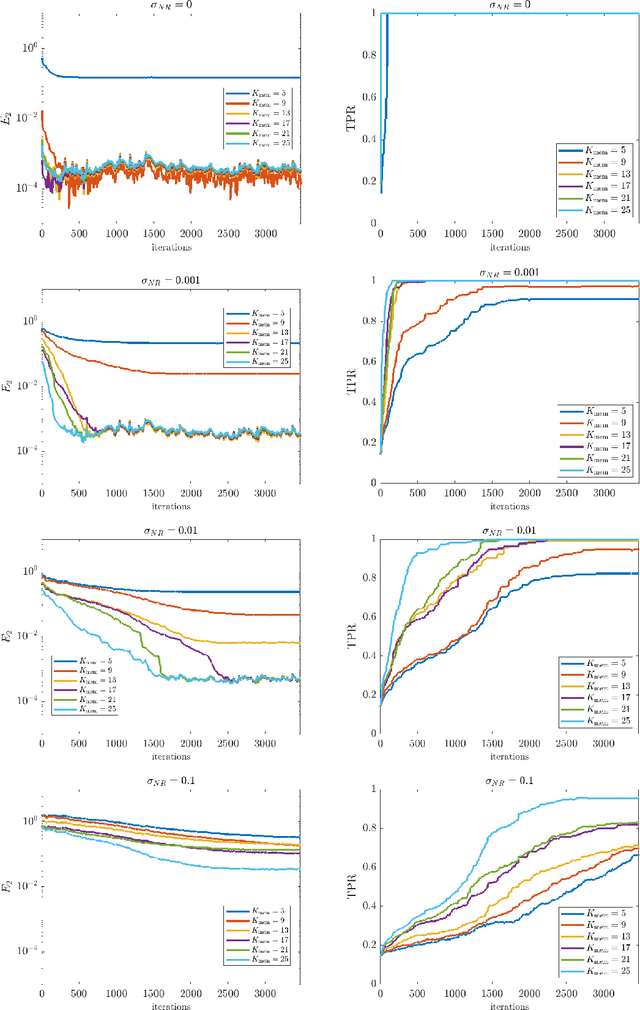
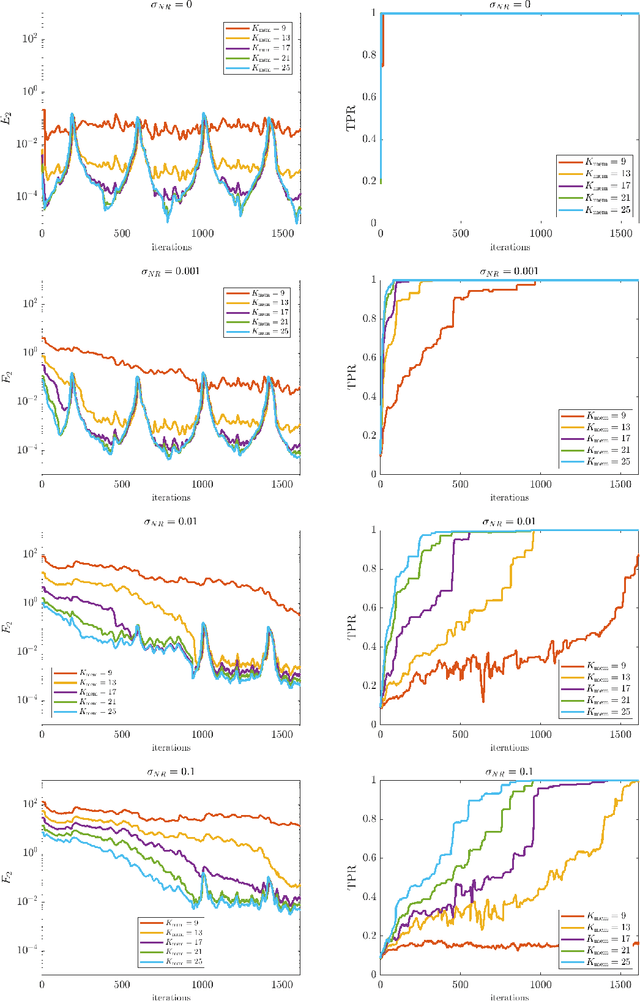
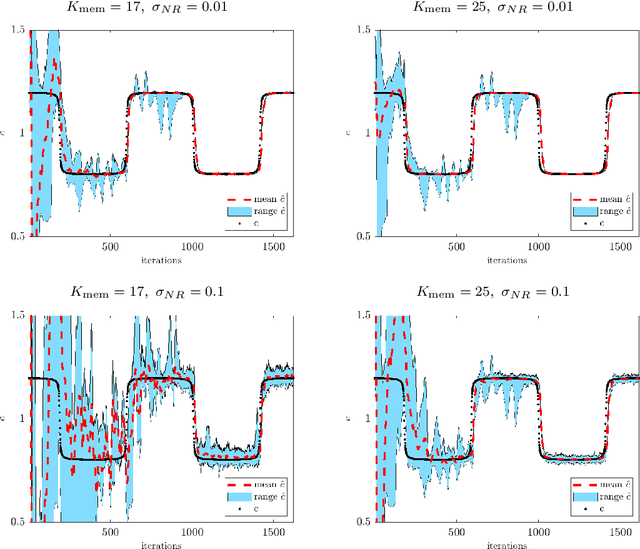
Abstract:This paper presents an online algorithm for identification of partial differential equations (PDEs) based on the weak-form sparse identification of nonlinear dynamics algorithm (WSINDy). The algorithm is online in a sense that if performs the identification task by processing solution snapshots that arrive sequentially. The core of the method combines a weak-form discretization of candidate PDEs with an online proximal gradient descent approach to the sparse regression problem. In particular, we do not regularize the $\ell_0$-pseudo-norm, instead finding that directly applying its proximal operator (which corresponds to a hard thresholding) leads to efficient online system identification from noisy data. We demonstrate the success of the method on the Kuramoto-Sivashinsky equation, the nonlinear wave equation with time-varying wavespeed, and the linear wave equation, in one, two, and three spatial dimensions, respectively. In particular, our examples show that the method is capable of identifying and tracking systems with coefficients that vary abruptly in time, and offers a streaming alternative to problems in higher dimensions.
Stochastic Saddle Point Problems with Decision-Dependent Distributions
Jan 07, 2022
Abstract:This paper focuses on stochastic saddle point problems with decision-dependent distributions in both the static and time-varying settings. These are problems whose objective is the expected value of a stochastic payoff function, where random variables are drawn from a distribution induced by a distributional map. For general distributional maps, the problem of finding saddle points is in general computationally burdensome, even if the distribution is known. To enable a tractable solution approach, we introduce the notion of equilibrium points -- which are saddle points for the stationary stochastic minimax problem that they induce -- and provide conditions for their existence and uniqueness. We demonstrate that the distance between the two classes of solutions is bounded provided that the objective has a strongly-convex-strongly-concave payoff and Lipschitz continuous distributional map. We develop deterministic and stochastic primal-dual algorithms and demonstrate their convergence to the equilibrium point. In particular, by modeling errors emerging from a stochastic gradient estimator as sub-Weibull random variables, we provide error bounds in expectation and in high probability that hold for each iteration; moreover, we show convergence to a neighborhood in expectation and almost surely. Finally, we investigate a condition on the distributional map -- which we call opposing mixture dominance -- that ensures the objective is strongly-convex-strongly-concave. Under this assumption, we show that primal-dual algorithms converge to the saddle points in a similar fashion.
OpReg-Boost: Learning to Accelerate Online Algorithms with Operator Regression
May 27, 2021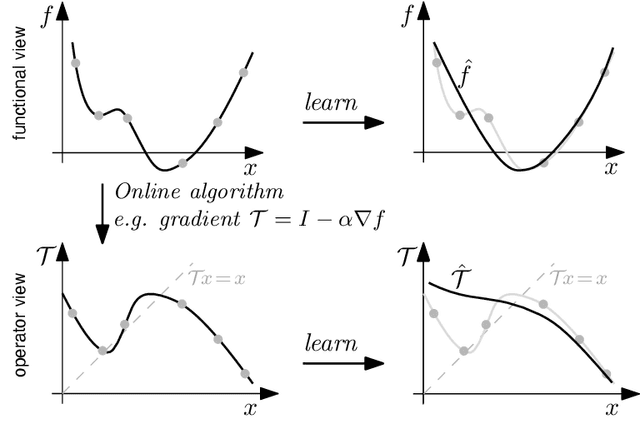
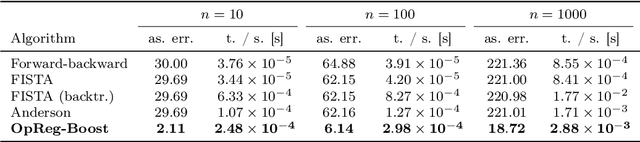
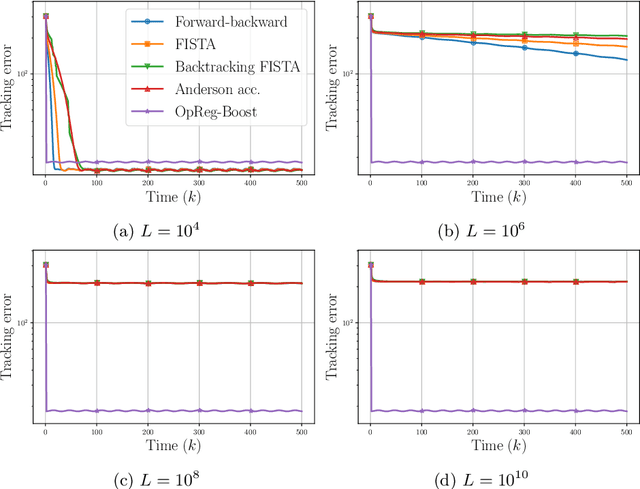
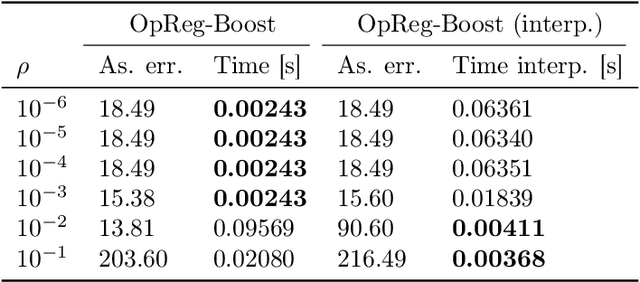
Abstract:This paper presents a new regularization approach -- termed OpReg-Boost -- to boost the convergence and lessen the asymptotic error of online optimization and learning algorithms. In particular, the paper considers online algorithms for optimization problems with a time-varying (weakly) convex composite cost. For a given online algorithm, OpReg-Boost learns the closest algorithmic map that yields linear convergence; to this end, the learning procedure hinges on the concept of operator regression. We show how to formalize the operator regression problem and propose a computationally-efficient Peaceman-Rachford solver that exploits a closed-form solution of simple quadratically-constrained quadratic programs (QCQPs). Simulation results showcase the superior properties of OpReg-Boost w.r.t. the more classical forward-backward algorithm, FISTA, and Anderson acceleration, and with respect to its close relative convex-regression-boost (CvxReg-Boost) which is also novel but less performing.
Optimization and Learning with Information Streams: Time-varying Algorithms and Applications
Oct 17, 2019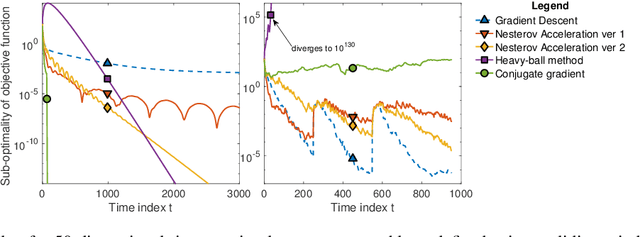
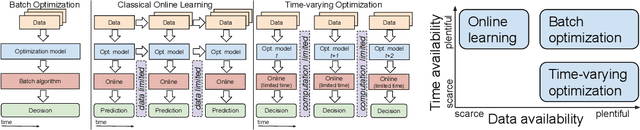


Abstract:There is a growing cross-disciplinary effort in the broad domain of optimization and learning with streams of data, applied to settings where traditional batch optimization techniques cannot produce solutions at time scales that match the inter-arrival times of the data points due to computational and/or communication bottlenecks. Special types of online algorithms can handle this situation, and this article focuses on such time-varying optimization algorithms, with emphasis on Machine Leaning and Signal Processing, as well as data-driven control. Approaches for the design of time-varying first-order methods are discussed, with emphasis on algorithms that can handle errors in the gradient, as may arise when the gradient is estimated. Insights on performance metrics and accompanying claims are provided, along with evidence of cases where algorithms that are provably convergent in batch optimization perform poorly in an online regime. The role of distributed computation is discussed. Illustrative numerical examples for a number of applications of broad interest are provided to convey key ideas.
Inexact Online Proximal-gradient Method for Time-varying Convex Optimization
Oct 04, 2019
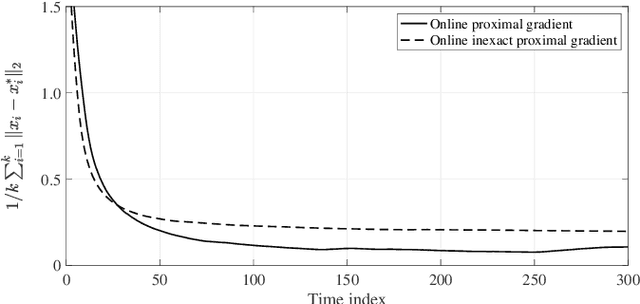
Abstract:This paper considers an online proximal-gradient method to track the minimizers of a composite convex function that may continuously evolve over time. The online proximal-gradient method is inexact, in the sense that: (i) it relies on an approximate first-order information of the smooth component of the cost; and, (ii) the proximal operator (with respect to the non-smooth term) may be computed only up to a certain precision. Under suitable assumptions, convergence of the error iterates is established for strongly convex cost functions. On the other hand, the dynamic regret is investigated when the cost is not strongly convex, under the additional assumption that the problem includes feasibility sets that are compact. Bounds are expressed in terms of the cumulative error and the path length of the optimal solutions. This suggests how to allocate resources to strike a balance between performance and precision in the gradient computation and in the proximal operator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge