Scalable Gaussian Process Hyperparameter Optimization via Coverage Regularization

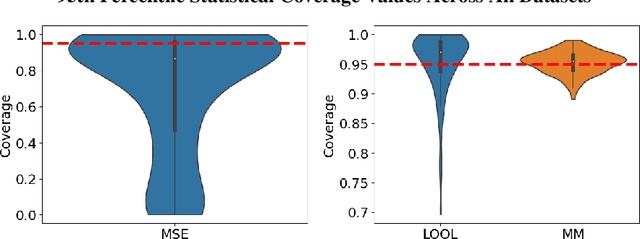
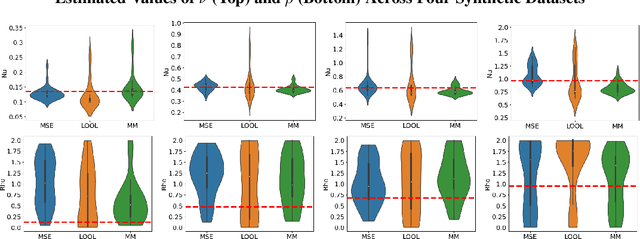
Gaussian processes (GPs) are Bayesian non-parametric models popular in a variety of applications due to their accuracy and native uncertainty quantification (UQ). Tuning GP hyperparameters is critical to ensure the validity of prediction accuracy and uncertainty; uniquely estimating multiple hyperparameters in, e.g. the Matern kernel can also be a significant challenge. Moreover, training GPs on large-scale datasets is a highly active area of research: traditional maximum likelihood hyperparameter training requires quadratic memory to form the covariance matrix and has cubic training complexity. To address the scalable hyperparameter tuning problem, we present a novel algorithm which estimates the smoothness and length-scale parameters in the Matern kernel in order to improve robustness of the resulting prediction uncertainties. Using novel loss functions similar to those in conformal prediction algorithms in the computational framework provided by the hyperparameter estimation algorithm MuyGPs, we achieve improved UQ over leave-one-out likelihood maximization while maintaining a high degree of scalability as demonstrated in numerical experiments.

Stochastic Saddle Point Problems with Decision-Dependent Distributions

This paper focuses on stochastic saddle point problems with decision-dependent distributions in both the static and time-varying settings. These are problems whose objective is the expected value of a stochastic payoff function, where random variables are drawn from a distribution induced by a distributional map. For general distributional maps, the problem of finding saddle points is in general computationally burdensome, even if the distribution is known. To enable a tractable solution approach, we introduce the notion of equilibrium points -- which are saddle points for the stationary stochastic minimax problem that they induce -- and provide conditions for their existence and uniqueness. We demonstrate that the distance between the two classes of solutions is bounded provided that the objective has a strongly-convex-strongly-concave payoff and Lipschitz continuous distributional map. We develop deterministic and stochastic primal-dual algorithms and demonstrate their convergence to the equilibrium point. In particular, by modeling errors emerging from a stochastic gradient estimator as sub-Weibull random variables, we provide error bounds in expectation and in high probability that hold for each iteration; moreover, we show convergence to a neighborhood in expectation and almost surely. Finally, we investigate a condition on the distributional map -- which we call opposing mixture dominance -- that ensures the objective is strongly-convex-strongly-concave. Under this assumption, we show that primal-dual algorithms converge to the saddle points in a similar fashion.